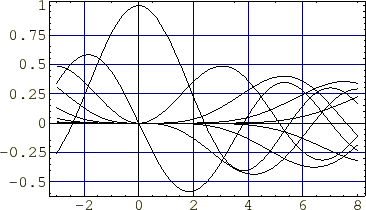
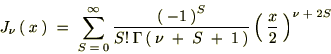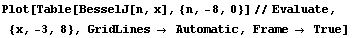��������p�����x�b�Z�����̓�����
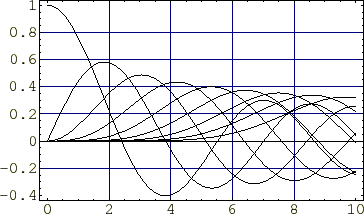
�w�����z���c�������ƌĂ�鎮�ɑ��A�~�����W��K�p�����ē�����������Ɏ��Ɏ������悤�Ȕ���������������܂��B
���̕������̂��Ƃ��x�b�Z���̔����������ƌĂт܂��B
���̔����������̉������߂ɂ͕��i�ʂ�̂������Ƃ��܂������Ȃ��̂ŁA���鋉������̉��Ƃ��ĉ��肷��������g������@�h�Ƃ������@���g���Ă��̉������߂Ă������ƂɂȂ�܂��B
�܂����Ƃ��Ă̋���������
���̔����������������Ă����ۂɂ����Ď��̂悤�ȋ��������ЂƂ܂��l���܂��B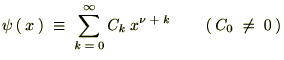
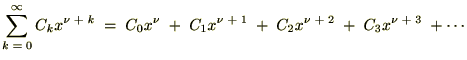
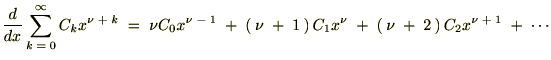
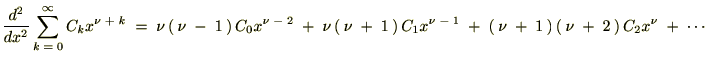
�܂Ƃ߂ĊȒP�ɕ\���Ǝ��̂悤�ȊW�����o�Ă��܂��B
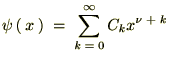
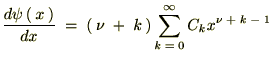
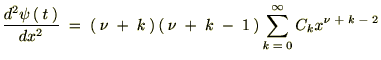
�������قǂ̃x�b�Z�������������̒��ɂ��ꂼ�������Ă����܂��B
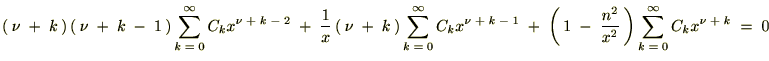
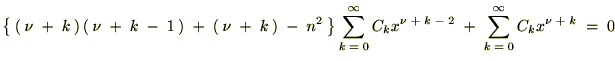
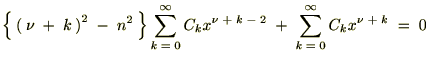
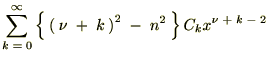
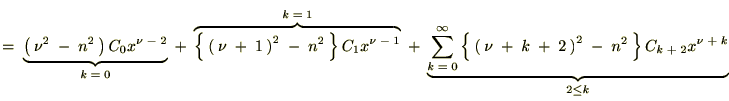
���A
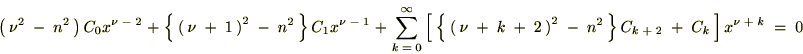
��P������A
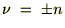 ���l�����āA
���l�����āA
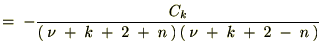

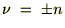 ���l�����āA
���l�����āA
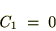
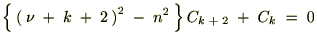
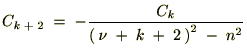
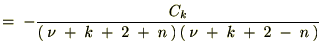
���Ɏ��̒���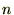 ��
��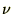 �Ɠ������̎����ƍl���Ď��̂悤�ɒu���܂��B
�Ɠ������̎����ƍl���Ď��̂悤�ɒu���܂��B
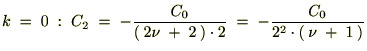
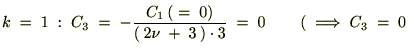
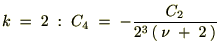
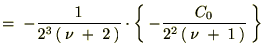
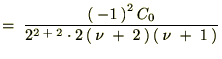
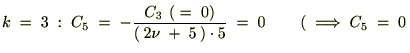
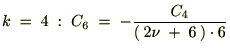
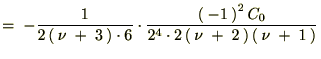
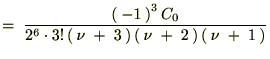
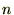 ��
��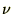 �Ɠ������̎����ƍl���Ď��̂悤�ɒu���܂��B
�Ɠ������̎����ƍl���Ď��̂悤�ɒu���܂��B
����Ď��̂悤�ɂȂ�܂��B
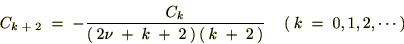
k��0���珇�ʑ�����Ă������̎��̕ω������Ă����܂��B
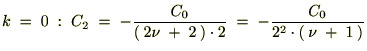
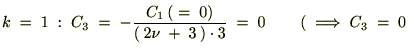
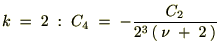
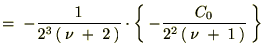
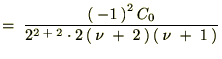
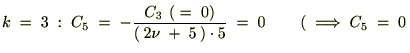
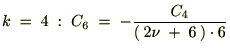
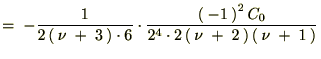
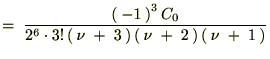
�����������ʂɂ�����̓[���ɂȂ�̂ł�����Ȃ����߂ɐV����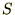 ��p�ӂ��āA
��p�ӂ��āA
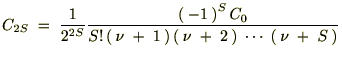
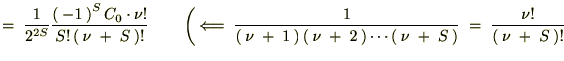
���̒���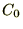 �����̂悤�ɒu���܂��B
�����̂悤�ɒu���܂��B
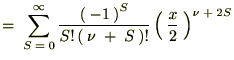
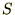 ��p�ӂ��āA
��p�ӂ��āA
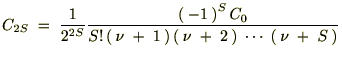
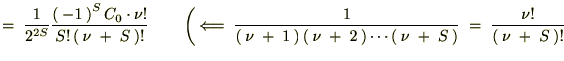
���̒���
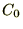 �����̂悤�ɒu���܂��B
�����̂悤�ɒu���܂��B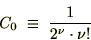
���̂��Ƃ���A
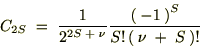
�ŏ��̎��ɓ��Ă͂߂�A
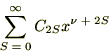
�ƂȂ���Ɖ��肵���ׂ������͎��̂悤�ɒu���܂��B
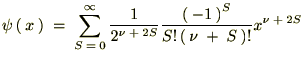
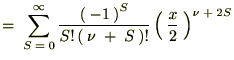
����Ɏ��Ɏ������悤�Ȑ��������K���}���ƌĂ����́A
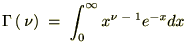
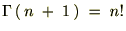
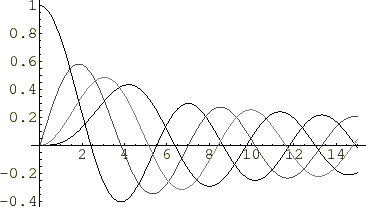
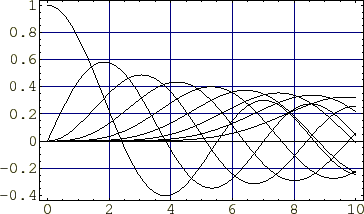
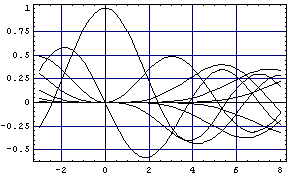
�x�b�Z�����̕`��
��K�x�b�Z�����̔����ό`
�x�b�Z������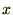 ��
��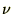 �悵�����̂��|���āA�����
�悵�����̂��|���āA�����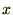 �Ŕ��������Ƃ��ǂ̂悤�Ȍ`�ɕό`�ł��邩���l�@���Ă݂܂��傤�B
�Ŕ��������Ƃ��ǂ̂悤�Ȍ`�ɕό`�ł��邩���l�@���Ă݂܂��傤�B
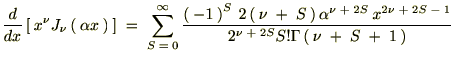
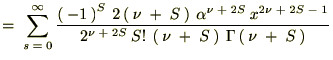
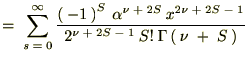
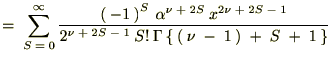
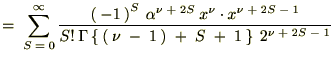
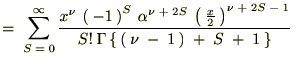
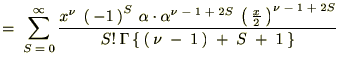
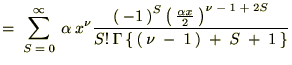
�ȒP�ɂ܂Ƃ߂�Ǝ��̂悤�Ȍ`�ɂȂ�܂��B
�Ȃ̂ł���肾���m���Ƃ��ƌ�X�y��������܂���̂ŁA�Ƃ肠�����y�����O���Ă݂܂����B
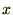 ��
��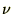 �悵�����̂��|���āA�����
�悵�����̂��|���āA�����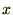 �Ŕ��������Ƃ��ǂ̂悤�Ȍ`�ɕό`�ł��邩���l�@���Ă݂܂��傤�B
�Ŕ��������Ƃ��ǂ̂悤�Ȍ`�ɕό`�ł��邩���l�@���Ă݂܂��傤�B
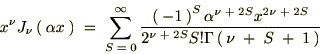
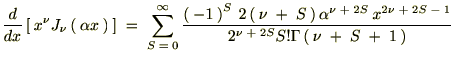
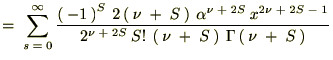
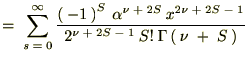
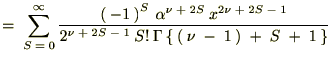
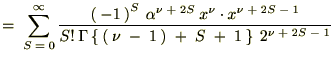
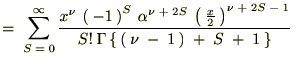
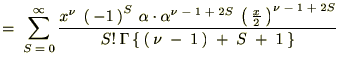
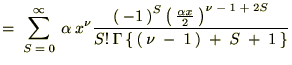
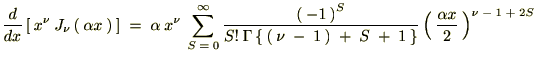
�r���A�ȉ��Ɏ����悤�ȃK���}���̐������g���Ă��܂��B
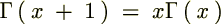
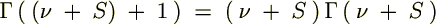
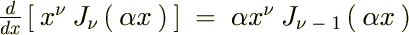
���̕ӂ̂Ƃ��͑債�����e�ł͂Ȃ��ł������������ό`�͗ʎq�͊w�̖��Ȃł��܂Ɏg���邱�Ƃ�����܂��B
�Ȃ̂ł���肾���m���Ƃ��ƌ�X�y��������܂���̂ŁA�Ƃ肠�����y�����O���Ă݂܂����B
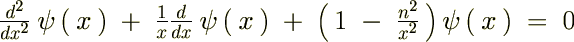
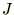 ��p���čŏI�I�Ɏ��̂悤�Ȋ������܂�܂��B
��p���čŏI�I�Ɏ��̂悤�Ȋ������܂�܂��B