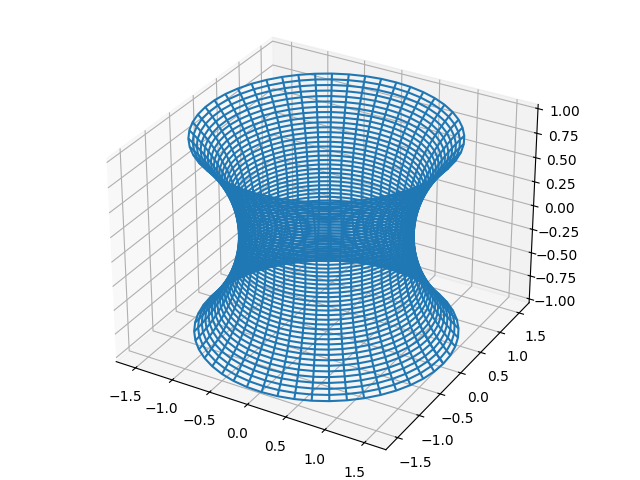
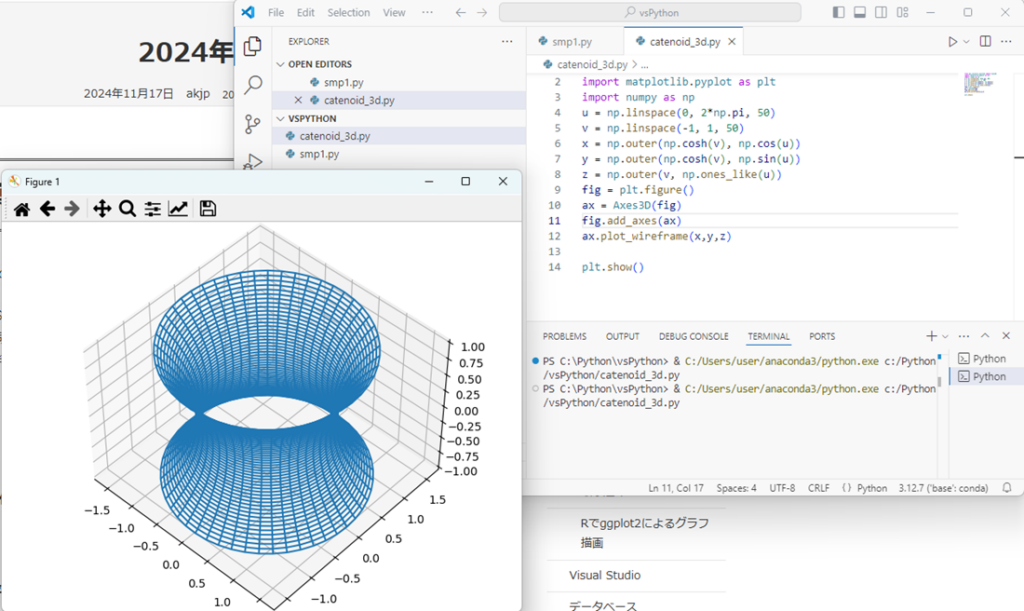
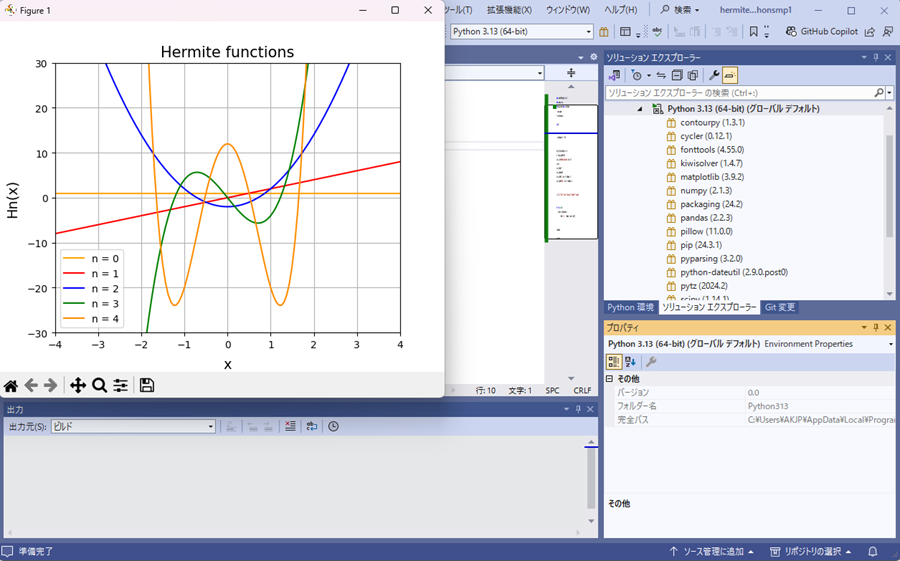
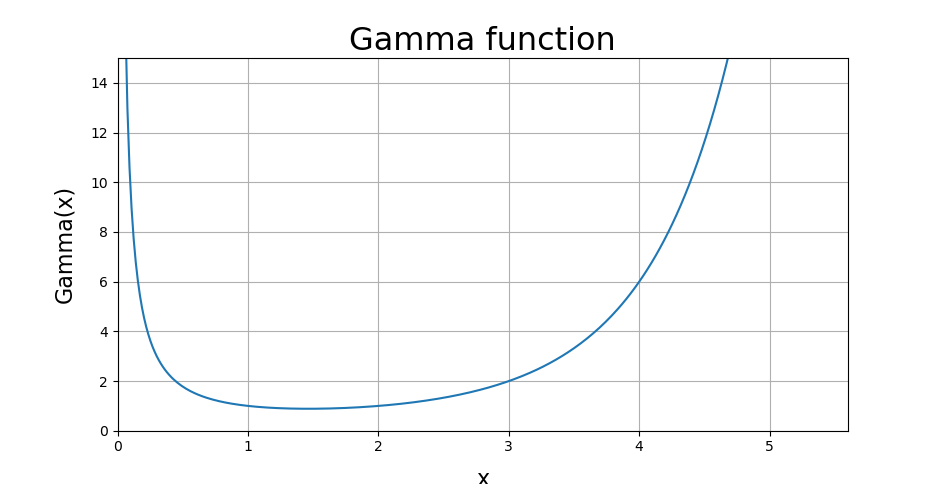
サテライトサイト微分方程式いろいろコンテンツトップページに使われた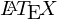 コードになります。コンパイル時のエラー等の修正は確認済みなのでこのまま自端末の
コードになります。コンパイル時のエラー等の修正は確認済みなのでこのまま自端末の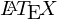 文書にコピペして貼り付けてDVIファイル出力すれば同様の数式画像が得られます。
文書にコピペして貼り付けてDVIファイル出力すれば同様の数式画像が得られます。
Mathematical.jp
当サイトは主に物理学、および数学を中心にしてその他の項目も含めた少々ごった煮のWebサイトになります。基本としてはわかりにくいものをわかりにくく説明するのではなく、Webという紙面による制限のない環境を最大限に利用し、途中の式変形過程を端折らずになるべく細かく、かつ詳しく説明しつつ、数学になじみがない方でも理解でき、決して鏤塵吹影にさせないコンテンツ作成を主眼とするサイトになります。

Mathematical.jpリニューアルに伴うお知らせ
当サイトは2000年代後半より運営されている物理および数学を中心にしたサイトになります。この度、諸事情によりMathematical.jpのコンテンツ分岐と、新システムへの入れ替えを目的としたシステム更新作業を実施したことをお知らせいたします(2024年7/13付)。
経緯と背景
運用を始めた十数年ほど前まではブラックショールズモデル、サルでもわかる線形代数、よくわかる慣性モーメント、よくわかるベクトル解析をはじめとした物理学および数学と、その他関連の内容を含むコンテンツを中心にした活動をしておりましたが、昨今のさまざまな状況(*)、さらにはサーバやフレームワークシステムの陳腐化が原因によって起きている慢性的なシステム障害および弊害への対応、また旧態依然のシステムでは日々進化し続けるIT環境に対応できないという理由のため、この度のシステム全体の刷新を目的とした新規サイトの構築公開に至りました。
主なサテライトサイト
(*)近年、よくわかる慣性モーメントを筆頭に以下サテライトサイトコンテンツの盗用が目立ちます。当サイトにおける文章や画像といったその他も含むコンテンツ関連を無断転載することを一切禁止します。明らかな盗用と思われるものに対しては、法的処置を行います。また引用する場合は必ずバックリンクを貼るなど社会人としての最低限のマナーとルールは守るようにしてください。

Moment of Inertia
M.O.I, also known as rotational inertia is a concept related to rotational motion. It quantifies an object’s resistance to changes in its.

Linear Algebra
Linear algebra is ubiquitous in theoretical physics for those involved in modern science. It is learned in elementary mathematics.
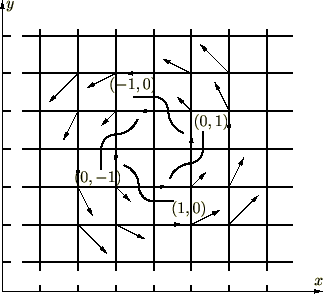
Vector Analysis
Vector analysis is physical mathematics using vectors and is an important theoretical concept utilized in various fields of modern physics.
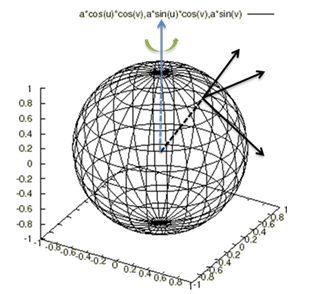
Differential Equations
A differential equation involves an independent variable, its functions, and its derivatives, and has general and particular solutions.
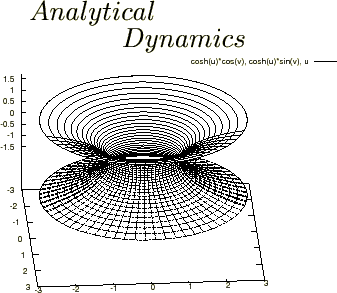
Analytical Mechanics
Invitation to Elegant Classical Physics – Physical mathematics expressed in a mathematically sophisticated form using analytical methods.
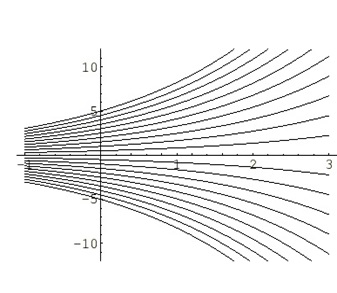
O.D.E
O.D.E refers to Ordinary Differential Equation. A differential equation that depends on a single independent variable.
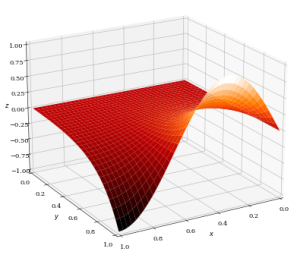
P.D.E
P.D.E refers to Partial Differential Equation. P.D.E is a mathematical equation that involves multiple independent variables
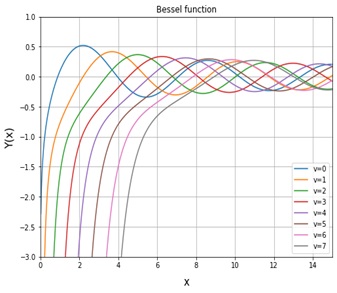
Bessel Function
Bessel functions, first defined by Bernoulli and then generalized by Bessel, are canonical solutions of Bessel’s differential equations.
Mathematical Statistics
Apply mathematics to statistics. Specific mathematical techniques used include linear algebra, stochastic analysis, and differential equations.
Black–Scholes model
The Black-Scholes option pricing model refers to the computational model required when pricing options in financial engineering.
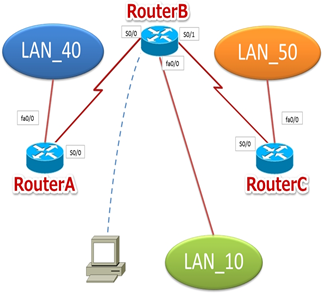
Network Engineer
Network engineers are information technicians who provide services in companies and organizations using routers and switches.
AKJP Prompt
Want to know more about other matters ? Learn more about knowledge and truth can mitigate burden of mind.
Then click here.
-
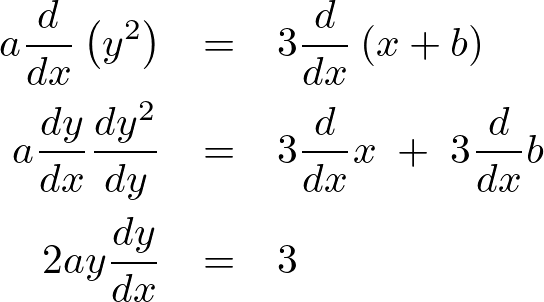
微分方程式いろいろTOPページLaTeXコード
続きを読む
-
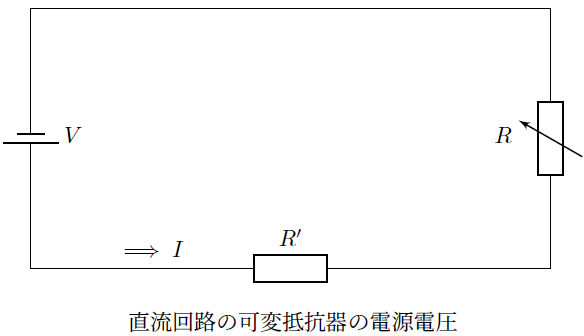
可変抵抗器の直列回路
続きを読む
-
Cisco Packet Tracer
続きを読む
-
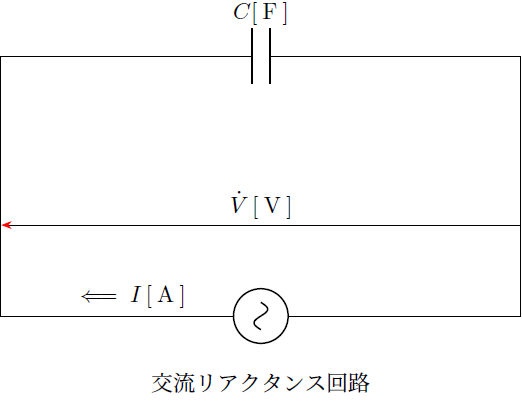
交流回路
続きを読む
-
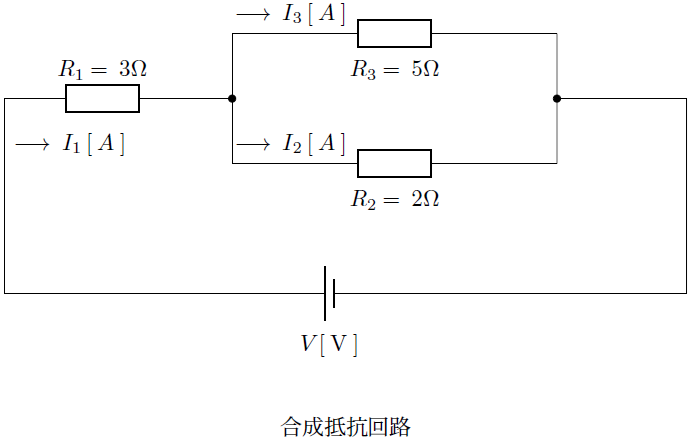
直流回路の合成抵抗
続きを読む
-
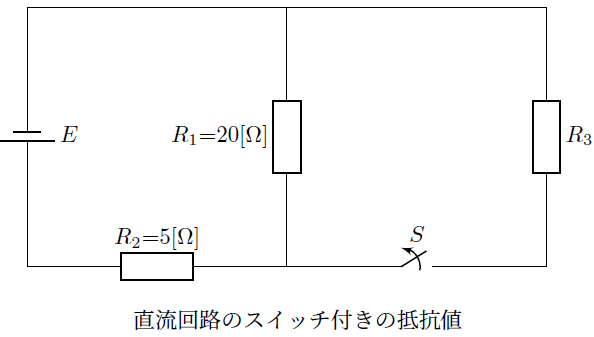
スイッチ付き回路素子の抵抗値
続きを読む
お知らせ
-
微分方程式いろいろTOPページLaTeXコード
カテゴリー : 微分方程式いろいろLaTeXコードサテライトサイト微分方程式いろいろコンテンツトップページに使われたコードになります。コンパイル時のエラー等の修…
-
-
微分方程式いろいろTOPページLaTeXコード
カテゴリー : 微分方程式いろいろLaTeXコードサテライトサイト微分方程式いろいろコンテンツトップページに使われたコードになります。コンパイル時のエラー等の修…
-
-
Cisco Packet Tracer
カテゴリー : Cisco Packet TracerPacket Tracerとは、Ciscoが提供するCisco製のルータやスイッチなどをローカル端末上でコンフ…
-
-
-
-
-
-
-