物理学
主に物理数学がメインになるかと思います。熱力学や宇宙物理学、さらには量子力学など様々な事項に関して扱っていこうかと思っております。更新は不定期です。
力学
コリオリと軽火器の話
アサルトライフルといった軽火器の場合の長距離射撃におけるコリオリの力について考察します。
コリオリ長距離弾道軌道計算
実際のコリオリ力を考慮した長距離弾道軌道計算を具体的に行っていきます。
宇宙物理学
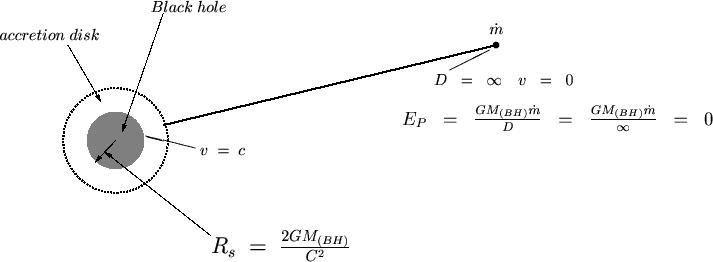
ブラックホールとクェーサー
元々は2ちゃんの科学ニューススレから見つけてきたものを取り扱ったものです。こうした事象に対する歴史的背景や数理論的な解釈などに関する解説なんかもあったらいいだろうなと思いましたので、今回はこれらの周辺知識についてやってみました。