���w���Y�^
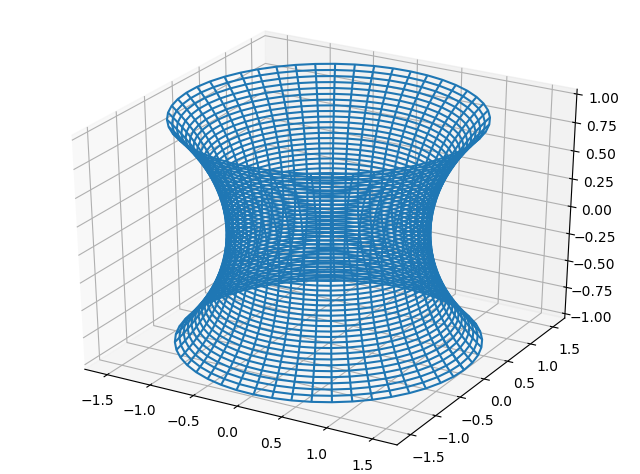
�y��O�́z�� �����������̊T�O
�������������Ƃ͎��̒��ɓƗ��ϐ��Ƃ��̊�����ɂ͂��̓������܂�ł�����̂��܂߂Ă����܂��B�����������������Ƃ������Ƃ͗^�����Ă��鎮���P���I�ɖ��������̂����߂邱�Ƃł���A���̉��ɂ͈�ʉ��ƁA����ɂ͔C�Ӓ萔�ɓ��ʂȒl�����ċ��߂������Ȃǂ�����܂��B����P�W�O�O�N�O��ɂ����Ĕ����ϕ��ƌĂ�鐔�w���삪�͂��܂�A����Ɠ����Ɍ������E�ɂ����鎩�R���ۂ̈��ʗ����𖾂�����̂Ƃ��Ĕ��W���Ă����w��Ȃ����ł��B
�����������͑�܂��ɕ����Č����Ǝ��̂Q�ɕ��ނ���܂��B
- �����������
������������|��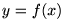 �Ƃ��̓���
�Ƃ��̓���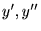 �ƓƗ��ϐ�
�ƓƗ��ϐ�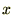 ���܂ޕ������������܂��B
���܂ޕ������������܂��B
�Ɨ��ϐ��̐��͈�̂��� - �Δ���������
�Δ����������|�����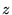 �̂Ȃ��ɕϐ���
�̂Ȃ��ɕϐ���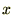 �Ȃ�
���̓������܂߂ĂQ�ȏ�̂悤�ȑ��ϐ����݂�����́B
�Ȃ�
���̓������܂߂ĂQ�ȏ�̂悤�ȑ��ϐ����݂�����́B
�y�����������̂������̗�z
��1
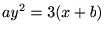
��L�̎��̗�����
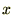 �ɑ��Ĕ������܂��B
�ɑ��Ĕ������܂��B

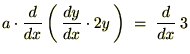
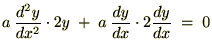
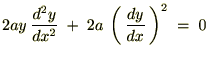
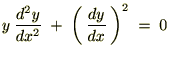
��2
�~�Ɋւ���l�@
���̉~�ɂ��čl�@���Ă݂܂��傤�B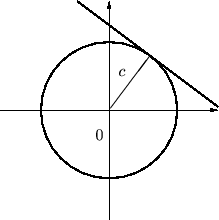
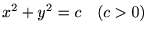 �ł��B�����
�ł��B�����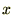 �Ŕ�������Ƃǂ��Ȃ�ł��傤���H
�Ŕ�������Ƃǂ��Ȃ�ł��傤���H���ۂɂ���Ă݂�ƁA
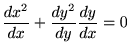
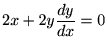
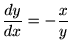
��3
�͊w�ւ̉��p
��l�ȏd�͏ꒆ�ɂ����鎿�_�̗͊w�I�G�l���M�[
�S�����̎����g���āA�͊w�I�G�l���M�[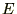 �����Ԃɂ�炸���A�܂�A
�����Ԃɂ�炸���A�܂�A
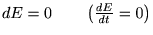
���Ȃ݂Ɏ��ԂŔ�������ꍇ��
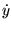 �ȂǂƂ��������������܂��B�Ӗ��I�ɂ�
�ȂǂƂ��������������܂��B�Ӗ��I�ɂ�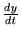 �ƑS�������ł��B�Ăѕ��̓h�b�g�Ƃ����܂��̂�
�ƑS�������ł��B�Ăѕ��̓h�b�g�Ƃ����܂��̂�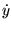 �̓��C�̃����h�b�g�ȂǂƂ������肵�܂��B
�̓��C�̃����h�b�g�ȂǂƂ������肵�܂��B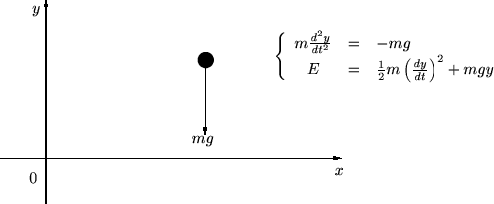
�͊w�I�G�l���M�[
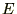 �̎��ɂ͕ϐ���
�̎��ɂ͕ϐ���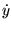 ��
��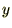 �̓�ɂȂ��Ă���̂�
�̓�ɂȂ��Ă���̂�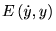 �ƕ\���܂��B
�ƕ\���܂��B����ɑ��đS�����̎���K�p����ƁA
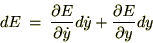
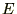 �̎������ꂼ��
�̎������ꂼ��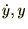 �ŕΔ������܂��B
�ŕΔ������܂��B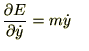
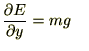
��قǂ̑S�����̎��ɂ���
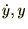 �̕Δ������������܂��B
�̕Δ������������܂��B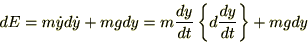
���̎����X�J���[�{
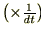 ���܂��B
���܂��B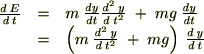
������
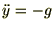 ���
��� 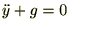
����ɂ��
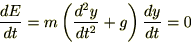
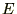 �h�͎��Ԃɂ�炸���ł���Ƃ������Ƃ��킩��܂����B
�h�͎��Ԃɂ�炸���ł���Ƃ������Ƃ��킩��܂����B
��L�ɂ������R���e���c�������������̊ȒP�ȎQ�l���x�̂��̂ł��B
�y���̃T�C�g�̎�|�z
���̃T�C�g�͊Ǘ��l�����Y�^�I�v�f�����˂Ȃ���O���ɃR���e���c�������A�b�v���[�h���Ă���T�C�g�ɂȂ�܂��B
���̕ӂ̂Ƃ�����������������������܂��悤��낵�����Ȃ����\���グ�܂��i�O�ցO�j��˯
�y���̃T�C�g�̎�|�z
���̃T�C�g�͊Ǘ��l�����Y�^�I�v�f�����˂Ȃ���O���ɃR���e���c�������A�b�v���[�h���Ă���T�C�g�ɂȂ�܂��B
�X�V�p�x�͐��T�Ԃ��琔������1�R���e���c���炢�ɂȂ邩�Ǝv���܂������݁A�Ǘ��l�����Z�̂��߂���ȏ�ɂȂ��Ă���܂��B
���̕ӂ̂Ƃ�����������������������܂��悤��낵�����Ȃ����\���グ�܂��i�O�ցO�j��˯
- (2017/12/17)���˒��e���O���v�Z�B���X�V���܂���
- (2017/12/10)���˒��e���O���v�Z�A���X�V���܂���
- (2017/12/03)���˒��e���O���v�Z�@���X�V���܂���
- (2017/11/04)�R���I���̗����X�V���܂���
- (2017/10/13)�����X�L�A�������v�Z���X�V���܂���










