�ő̌��q�̔M�U���ƃf�������v�e�B�̖@��
���q�ǂ������K���������z�u����Ă���ő̌��q�ɂ����Ẳ^���i�M�U���j�ɂ��čl�@���܂��B
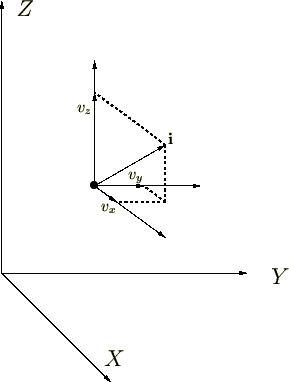
����ő̓��̌��q�̐����m����Ƃ�����A���A���������ꂼ����l��������v�łR�m�̐U���q������ƍl���邱�Ƃ��o���܂��B
����U���q�ɂ��āA���̕��t�ɂ�����^���G�l���M�[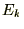 �ƁA�����Ĉʒu�G�l���M�[
�ƁA�����Ĉʒu�G�l���M�[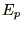 �����߂Ă݂Ă��ꂼ����r���܂��B
�����߂Ă݂Ă��ꂼ����r���܂��B
�^���G�l���M�[
�܂����t�̒��S�ʒu��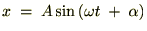 �Ƃ��Ă��ň�x��������A
�Ƃ��Ă��ň�x��������A
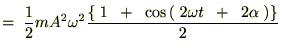
���̂Ƃ��̎����s��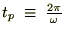 �Ƃ�����
�Ƃ�����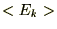 ���v�Z���Ă����܂��B
���v�Z���Ă����܂��B
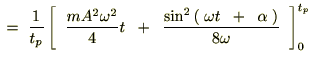
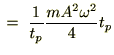


����ő̓��̌��q�̐����m����Ƃ�����A���A���������ꂼ����l��������v�łR�m�̐U���q������ƍl���邱�Ƃ��o���܂��B
����U���q�ɂ��āA���̕��t�ɂ�����^���G�l���M�[
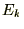 �ƁA�����Ĉʒu�G�l���M�[
�ƁA�����Ĉʒu�G�l���M�[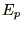 �����߂Ă݂Ă��ꂼ����r���܂��B
�����߂Ă݂Ă��ꂼ����r���܂��B
�^���G�l���M�[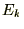
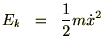
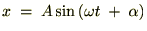 �Ƃ��Ă��ň�x��������A
�Ƃ��Ă��ň�x��������A
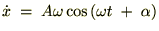
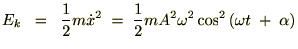
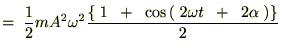
���̂Ƃ��̎����s��
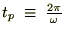 �Ƃ�����
�Ƃ�����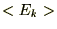 ���v�Z���Ă����܂��B
���v�Z���Ă����܂��B
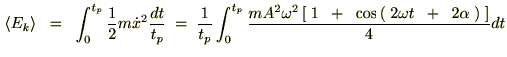
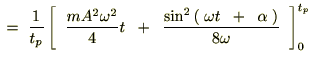
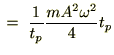


�ʒu�G�l���M�[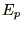
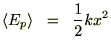
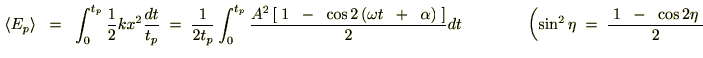
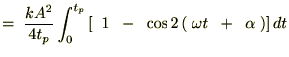
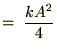
���̌��ʂɂ���āA
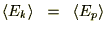
�܂��A�G�l���M�[�����z�̖@���ɂ��
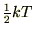 �̃G�l���M�[���z����̂ŁA
�̃G�l���M�[���z����̂ŁA

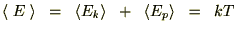
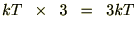
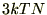 �ƂȂ�܂��B
�P�����̌��q�ł�
�ƂȂ�܂��B
�P�����̌��q�ł�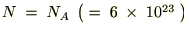
�G�l���M�[
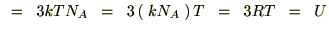
���̊W�ɂ�莟�̂悤�Ȃ��Ƃ����藧���܂��B
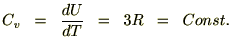
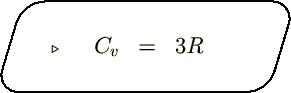
���̎��͎�����荂�����x�ł悭�������A
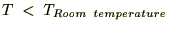 �ɂ����ẮA
�ɂ����ẮA
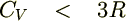
�Ɣ������܂��B
���ቷ�̏ꍇ
��قǂ̃f���[����-�v�e�B�̖@���͍����ł͂悭���藧���܂����ቷ�ɂ����Ă͂��̑���l���@���̒l��肩�Ȃ菬�����Ȃ邱�Ƃ��킩���Ă��܂��B���������Ƃ��̐U���q�̎��G�l���M�[��
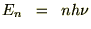 �i���F�v�����N�萔�j�Ƃ��A���̃G�l���M�[�̒l�͂��̐����l�̂ƂтƂт̒l���Ƃ�̂��Ƃ��܂��B�ڂ����ߒ��͐��̃e�L�X�g�ɔC����Ƃ��āA���̃G�l���M�[�����U���q�̐��̕��ϒl�͎��̂悤�Ȏ��ŗ^�����܂��B
�i���F�v�����N�萔�j�Ƃ��A���̃G�l���M�[�̒l�͂��̐����l�̂ƂтƂт̒l���Ƃ�̂��Ƃ��܂��B�ڂ����ߒ��͐��̃e�L�X�g�ɔC����Ƃ��āA���̃G�l���M�[�����U���q�̐��̕��ϒl�͎��̂悤�Ȏ��ŗ^�����܂��B
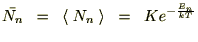
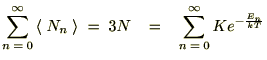
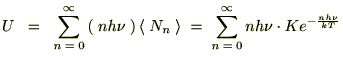
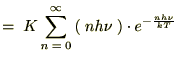
������
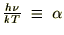 �ƒu����
�ƒu����
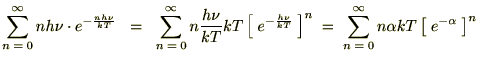
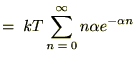
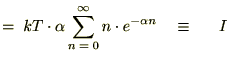
������ɁA
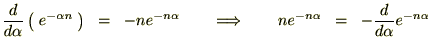
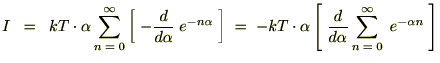
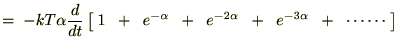
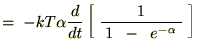
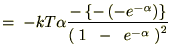
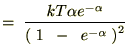
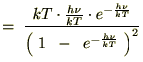
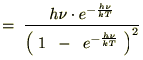
���Ȃ݂ɓr���̎��Ŏ��̂悤�ȕ��@���g���Ă��܂��B
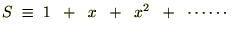
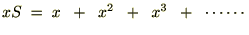
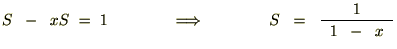
�����ŃG�l���M�[�U���q�̕��ϒl�Ɏ��������ƁA
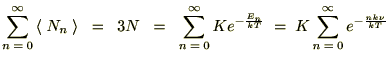
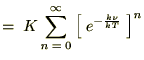
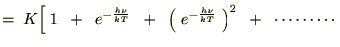
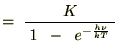
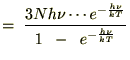
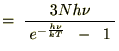
������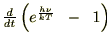 �̔����͎��Ɏ����悤�ȍ������������{���܂��B
�̔����͎��Ɏ����悤�ȍ������������{���܂��B
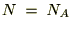 �̃A�{�K�h�����ɂƂ�A���̎�������ɕό`�����܂��B
�̃A�{�K�h�����ɂƂ�A���̎�������ɕό`�����܂��B
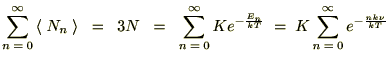
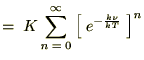
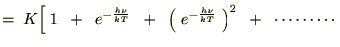
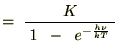
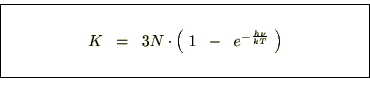
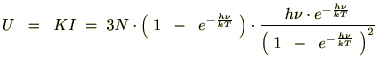
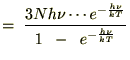
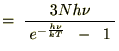
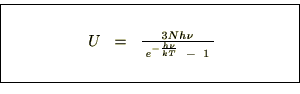
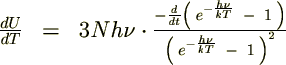
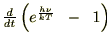 �̔����͎��Ɏ����悤�ȍ������������{���܂��B
�̔����͎��Ɏ����悤�ȍ������������{���܂��B
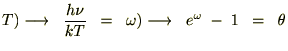
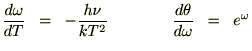
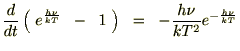
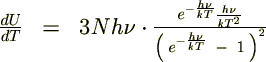
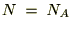 �̃A�{�K�h�����ɂƂ�A���̎�������ɕό`�����܂��B
�̃A�{�K�h�����ɂƂ�A���̎�������ɕό`�����܂��B
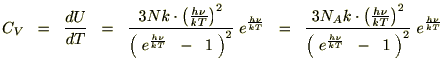
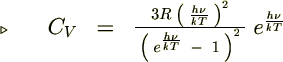
�����̏ꍇ
�����̏ꍇ�A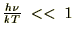 �ł���̂ŃC�N�X�|�[�l���V�����̐����ɂ��A
�ł���̂ŃC�N�X�|�[�l���V�����̐����ɂ��A

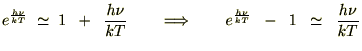
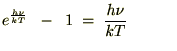
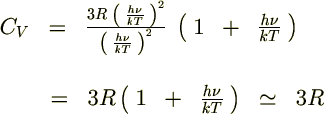
�ቷ�̏ꍇ
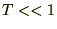 �ł���̂�
�ł���̂�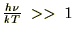 ����ɂ��A
����ɂ��A
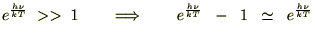
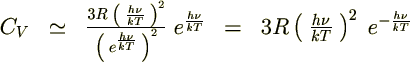
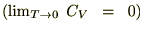
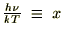 �ƒu����
�ƒu����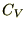 �������
�������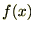 �Ƃ����������ɂ��Ă�������Ŕ������ċɒl�����߂�Ǝ��̂悤�ɂȂ�܂��B
�Ƃ����������ɂ��Ă�������Ŕ������ċɒl�����߂�Ǝ��̂悤�ɂȂ�܂��B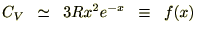
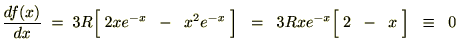
�ő̌��q�̔M�U���֘A�y�[�W
- ��ԕ�����
- ���낢��Ȕ������������������T�C�g�ł��B�l�I�Ȏ�̗̈�ł���Ă���̂ł��Ȃ�E���������e�����邩�Ǝv���܂����A���̂ւ�̂Ƃ���͐�������������C�ł��Ȃ������܂��B
- �}�b�N�X�E�F���̑��x���z��
- ���낢��Ȕ������������������T�C�g�ł��B�l�I�Ȏ�̗̈�ł���Ă���̂ł��Ȃ�E���������e�����邩�Ǝv���܂����A���̂ւ�̂Ƃ���͐�������������C�ł��Ȃ������܂��B
- �}�b�N�X�E�F���W��
- ���낢��Ȕ������������������T�C�g�ł��B�l�I�Ȏ�̗̈�ł���Ă���̂ł��Ȃ�E���������e�����邩�Ǝv���܂����A���̂ւ�̂Ƃ���͐�������������C�ł��Ȃ������܂��B











