�K�E�X�ϕ�
������Ԃɂ�����ϕ��ő��ɃK�E�X�ϕ��ƌ�������̂�����܂��B
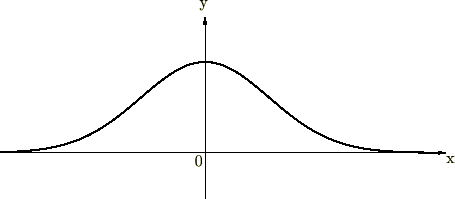
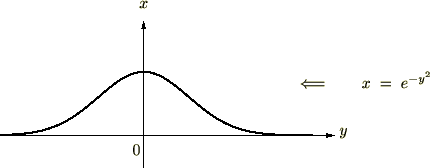
���}�͎w����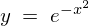 ��`�悵�����̂ł��B
��`�悵�����̂ł��B
���̊���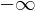 ����
����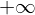 �͈̔͂ɂ����Đϕ������s����ǂ��Ȃ�ł��傤���H
�͈̔͂ɂ����Đϕ������s����ǂ��Ȃ�ł��傤���H
���̓�����P�������ɏ����Ǝ��̂悤�ɂȂ�܂��B
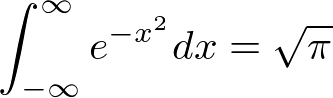
�͂��߂Č������͑����������Ǝv���܂��������������ʂ��m���ɂ܂���ʂ��Ă��܂��B
���̂��߂��̐ϕ��̂��Ƃ��A�K�E�X�̃C���`�L�ϕ��ȂǂƂ������肷����̂����܂ɂ��܂��B
�����ł͑�w�Ŏ��Ƃ��̎����̍u�`�m�[�g���Q�l�ɐ����������Ƃ������܂��B
�܂��ϕ�����͈͂�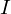 �ƒu���܂��B
�ƒu���܂��B
����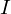 ���Q�悵�����̂ɑ��ċɍ��W�A
���Q�悵�����̂ɑ��ċɍ��W�A
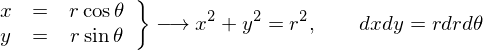
��K�p���܂����A�����ŁA
�Ƃ��Ă������l�i�ϕ��̈�j�ł���Ƃ������Ƃ͂킩��܂��B
�ł��̂Ŏ��̂悤�ɕ\���ł��邱�ƂɂȂ�܂��B
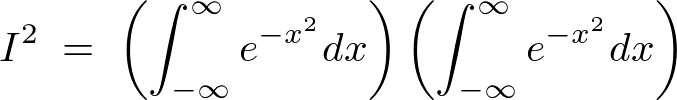
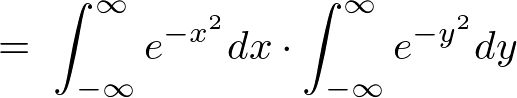
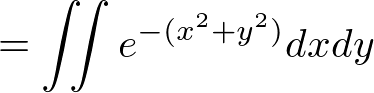
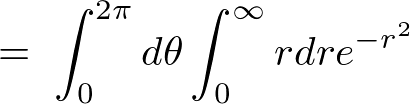
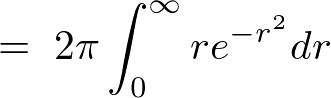
������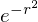 ���������Ɓi�ϐ��ϊ������āj�A
���������Ɓi�ϐ��ϊ������āj�A
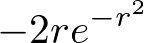
����ɂ��
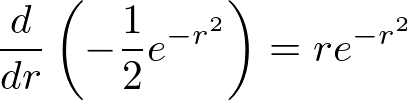
�Ȃ̂ł�����g���āA
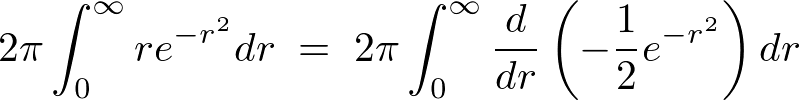
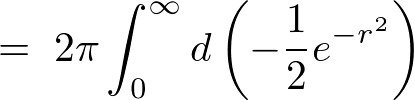
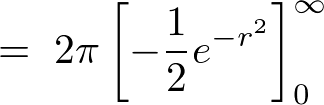
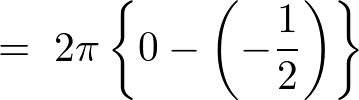

�ƂȂ�̂�I��2��͎��̂悤�ɋ��܂�܂��B
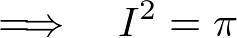
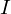 �͐��Ȃ̂�
�͐��Ȃ̂�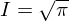
����āA
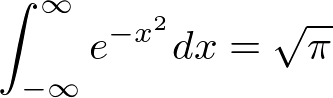
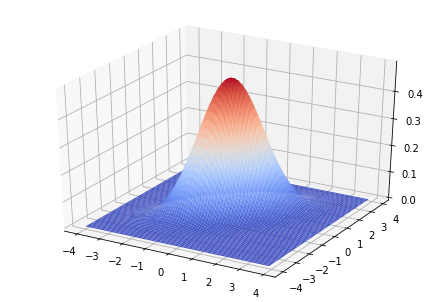
�K�E�X�ϕ��֘A�y�[�W
- ����
- ���̃Z�N�V�����ł͓����̊�{�I�ȍl�����Ƃ��̌v�Z���@�ɂ��čl�@���Ă����܂��B
- �������̔���
- �����ϕ��w�ɂ����ďd�v�ȊT�O�ł��鍇�����̊T�O�Ƃ��̔������@�Ɋւ��čl�@���Ă����܂��B
- �ΐ������@
- �ΐ������@�Ƃ͗��ӂ̑ΐ����Ƃ邱�Ƃ��疼�Â���ꂽ�����@�ł���A���̔������s���ꍇ�A�������̔��������s����ۂɗp����ꂽ�A�����Ƃ����l�������d�v�ɂȂ�܂��B
- ����
- �����ϕ��w�|�u���b�N�V���[���Y�Δ��������������߂̕Δ����Ɋւ��čl�@���Ă����܂��B1�̎��̒���2�̕ϐ��������Ă��邠����ɑ��Ă̔���h�_�@�ɂ��čl�@���Ă����܂��B
- �S����
- �S�����Ƃ͂��ׂĂ̕ϐ�������ʓ��������Ƃ��̈ꎟ�ߎ��ł̊��̕ω��ʂ�\���܂��B���̃Z�N�V�����ł͑S�����ɂ����邻�̍l�����Ƌ�̓I�Ȍv�Z���@�ɂ��čl�@���Ă����܂��B
- ��ϐ����̐ϕ�
- ���T�C�g�͂��̃u���b�N�V���[���Y�Δ����������̓��o�ƒ낾���ł͂Ȃ����������߂̏������w����J�ɉ�������T�C�g�ɂȂ�܂��B���̃`���v�^�[�ł͊�{�ƂȂ镪��ɂȂ�����ϕ��Ɋւ��ĊȒP�ɐ������Ă����܂��B
- �u���ϕ�
- �Ԑ��F�L�̐ϕ��Ƃ����͎̂�ɐϕ��̌������g����悤�ɕό`������Ƃ����s�ׂ����ɏd�v�ɂȂ��Ă��܂��B���̃`���v�^�[�ł͂��̒n�Ԑ��ϕ��ɂ��Ċ����ɐ������Ă����܂��B
- �����ϕ�
- ���T�C�g�͂��̃u���b�N�V���[���Y�Δ����������̓��o�ƒ낾���ł͂Ȃ����������߂̏������w����J�ɉ�������T�C�g�ɂȂ�܂��B���̃`���v�^�[�ł͊�{�ƂȂ镪��ɂȂ�����ϕ��Ɋւ��ĊȒP�ɐ������Ă����܂��B


























