�S����
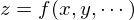 �@�|�@���ׂĂ̕ϐ�������ʓ������Ƃ�������
�@�|�@���ׂĂ̕ϐ�������ʓ������Ƃ�������
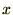 �������
�������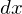 �����������B
�����������B

����ƁA�ꎟ�ߎ����A
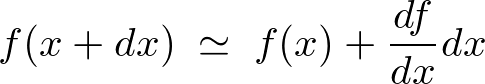
�ƂȂ�܂��B
�����ł��̂Ƃ��̊��̕ω��ʂ�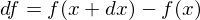 �Ə����Ȃ�A
�Ə����Ȃ�A
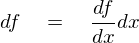
�ƂȂ�܂��B
�������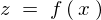 �̑S�����Ƃ����܂��B
�̑S�����Ƃ����܂��B
�S�����Ƃ́A���ׂĂ̕ϐ�������ʓ��������Ƃ��̈ꎟ�ߎ��ł̊��̕ω���
2�ϐ�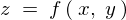 �̏ꍇ
�̏ꍇ
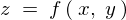 �̕ϐ�
�̕ϐ�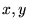 ������ʓ������Ă݂܂��B
������ʓ������Ă݂܂��B

����ƈꎟ�ߎ��ł́A
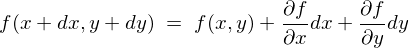
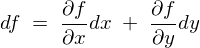
�R�ϐ�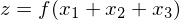 �ł������悤�ɁA
�ł������悤�ɁA
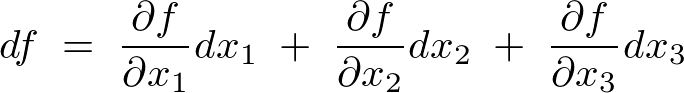
�����ŊȒP�ȗ����l���Ă܂��B
����Q�ϐ���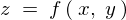 ���������Ƃ��܂��B���̕ϐ�
���������Ƃ��܂��B���̕ϐ�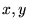 �͂���ɕϐ�
�͂���ɕϐ� �ɂ���Ď��������̂Ƃ��܂��B
�ɂ���Ď��������̂Ƃ��܂��B
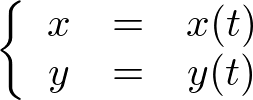
���̂Ƃ��̔����ω��ʂ́A���ꂼ��A
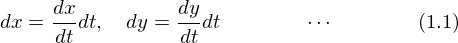
�ɂȂ�܂��B
�܂��A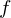 �ɑ���S�����́A
�ɑ���S�����́A
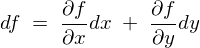
�Ȃ̂ŁA���̎��ɐ�قǂ�(1.1)�̎��������܂��B
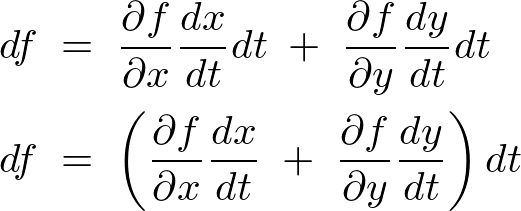
�܂��́A
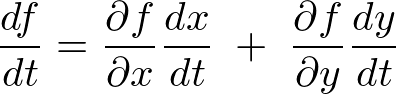
�ƂȂ�܂��B
�܂��A��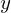 ���ϐ�
���ϐ� �ŕ\����Ă��鎟��
�ŕ\����Ă��鎟��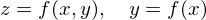 �Ƃ����悤�ȏꍇ�́A
�Ƃ����悤�ȏꍇ�́A
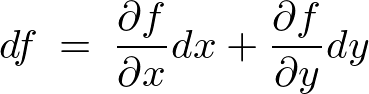
�����ŁA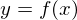 ����
����
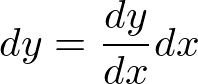
�Ȃ̂ł����������ƁA
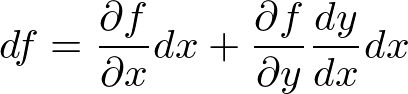
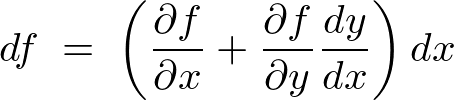
�ƂȂ�܂��B
�y���z
����Q�ϐ���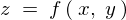 ������܂��B
������܂��B
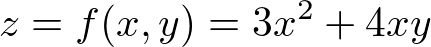
���̊��ɂ�����ϐ�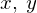 �͂��ꂼ�ꎟ�̂悤�ɕ\����Ƃ��܂��B
�͂��ꂼ�ꎟ�̂悤�ɕ\����Ƃ��܂��B
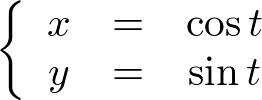
���̂Ƃ��A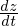 �����߂Ă݂܂��傤�B
�����߂Ă݂܂��傤�B
�y�����z
�܂��A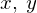 �̎���������܂��B
�̎���������܂��B
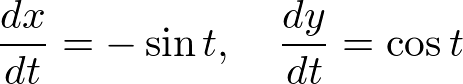
�����āA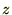 �̎��Ɋւ��Ă��ꂼ��
�̎��Ɋւ��Ă��ꂼ�� ��
��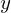 �ŕΔ������܂��B
�ŕΔ������܂��B
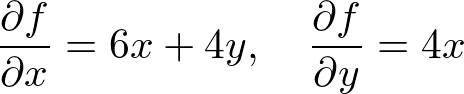
�����ŁA
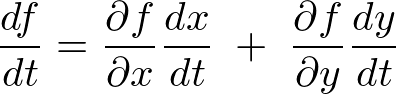
�ɑ������A
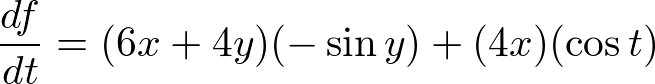
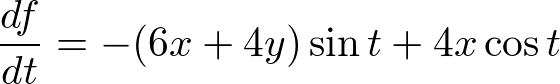
�ȏ�̍l����������ɔ��W�����Ă݂܂��傤�B
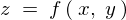 �ɂ�����
�ɂ�����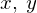 ���ϐ�
���ϐ�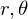 �ɂ��ꂼ��ˑ�����ꍇ
�ɂ��ꂼ��ˑ�����ꍇ
���Ɏ����悤�ɁA�����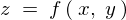 �ɂ�����
�ɂ�����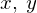 ������ɕϐ�
������ɕϐ�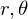 �ɂ��ꂼ��ˑ�����ꍇ���l���܂��B
�ɂ��ꂼ��ˑ�����ꍇ���l���܂��B
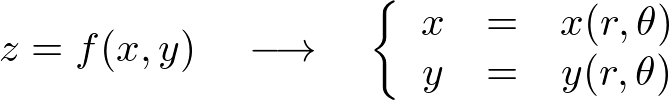
���̎��̑S�������ǂ��Ȃ邩���l���܂��B
�܂��A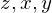 �̂��ꂼ��̑S�����̎��́A
�̂��ꂼ��̑S�����̎��́A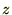 �̎��͕ϐ�
�̎��͕ϐ�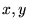 �Ɉˑ����Ă���̂ŁA
�Ɉˑ����Ă���̂ŁA

�����č��x�́A���� ��
��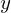 ���A���ꂼ��
���A���ꂼ��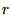 ��
��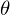 �Ɉˑ����Ă���̂�
�Ɉˑ����Ă���̂�
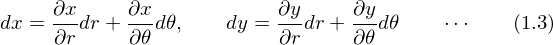
�ƂȂ�܂��B
(1.2)�̎���(1.3)�̂��ꂼ��̎��������Ă݂�ƁA
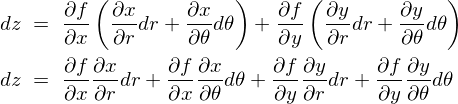
���A
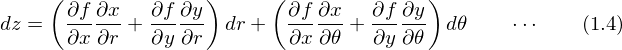
������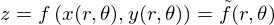 �Ƃ݂Ȃ���̂ŁA
�Ƃ݂Ȃ���̂ŁA

(1.4)�y��(1.5)�̎����r����A
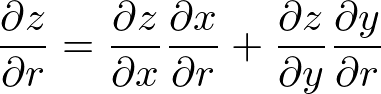
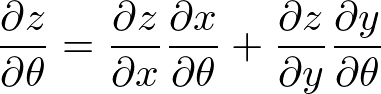
�ƕ\���邱�Ƃ��킩��܂��B
�ȏ�����Ɏ��ۂ̌v�Z���s���Ă݂܂��傤�B
�y���z
�����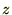 �̕ϐ�
�̕ϐ�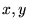 �����Ɏ����ϐ�
�����Ɏ����ϐ�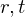 �ɂ���Ĉˑ����Ă���Ƃ��܂��B
�ɂ���Ĉˑ����Ă���Ƃ��܂��B
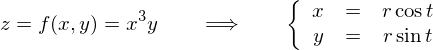
���̂��̂����߂Ă݂܂��傤�B
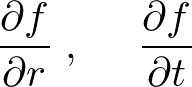
�y�����z
���ꂼ��̔����̌��ʂ�������
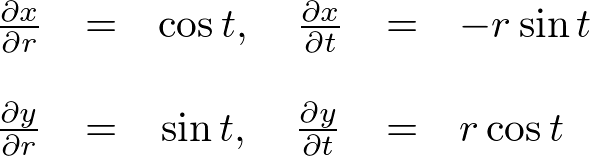
�����������A
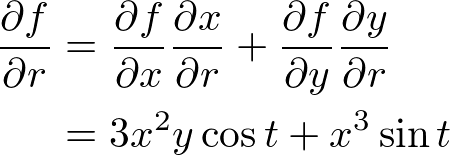
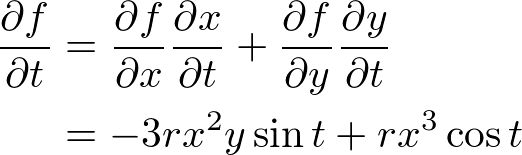
���A���̂悤�Ȍ��ʂ܂��B
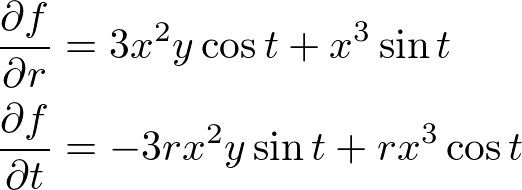
���
���̃Z�N�V�������ɂ����Ă������͒P�Ȃ���ł��B�����̂���������ǂ�ł݂Ă��������B
���܁A��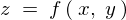 �ɍ\������Ă���ϐ�
�ɍ\������Ă���ϐ�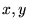 �́A�����
�́A�����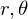 �Ƃ����ϐ��Ǝ��̂悤�ȊW�ɂ���Ƃ��܂��B
�Ƃ����ϐ��Ǝ��̂悤�ȊW�ɂ���Ƃ��܂��B
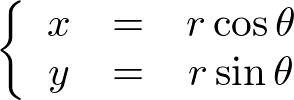
���̂Ƃ���
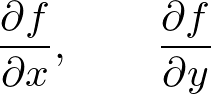
��
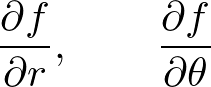
���g���ĕ\���Ƃǂ��Ȃ邩���������l�@���Ă݂܂��傤�B
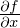 ��
��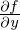 �͑S�����̌����ɂ��A
�͑S�����̌����ɂ��A
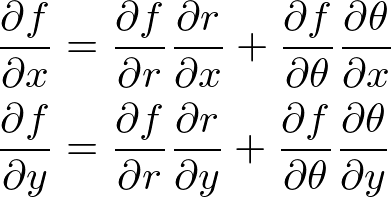
 ��
��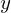 ��
��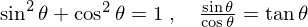 �Ƃ��������ɂ��A
�Ƃ��������ɂ��A
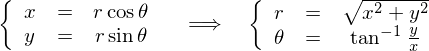
�Ə����Ȃ������Ƃ��o���܂��B
�܂��� �̂ق�����������Ă����܂��B
�̂ق�����������Ă����܂��B
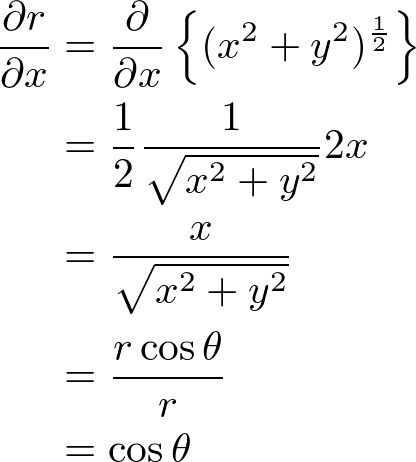
���ɁA
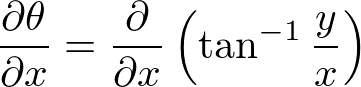
�̌v�Z�ł����A����͂�����ƍH�v���āA
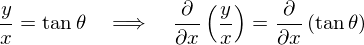
���̂悤�ɂ��A���ӂ����ꂼ��������܂��B
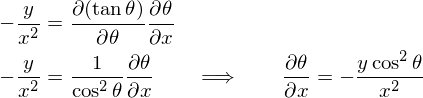
�ƂȂ�̂ŁA
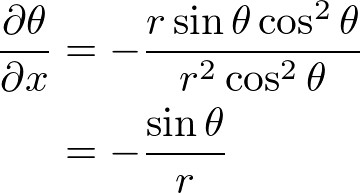
�����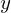 �Ɋւ��Ă̔������s���ƁA
�Ɋւ��Ă̔������s���ƁA
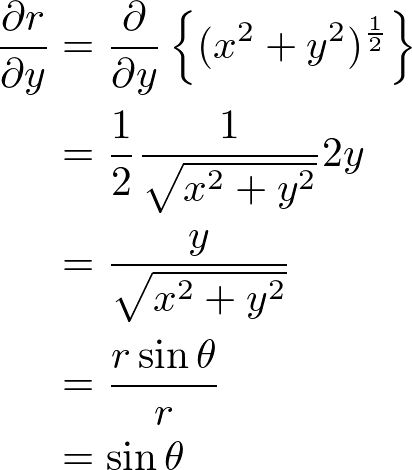
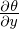 �́A��قǂƓ����悤�ɁA
�́A��قǂƓ����悤�ɁA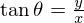 �̗��ӂ����x��
�̗��ӂ����x��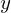 �ŕΔ������܂��B
�ŕΔ������܂��B
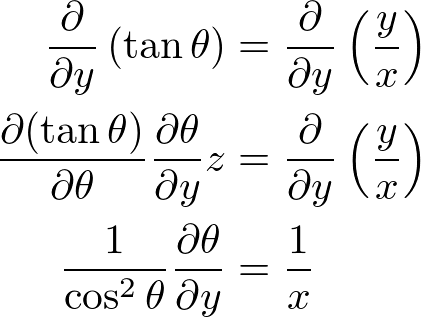
������A
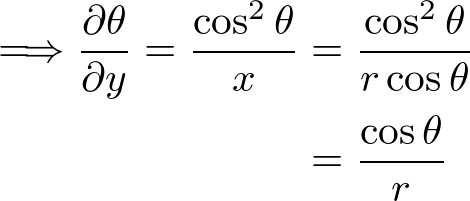
�ȏ�̌��ʂ��A���ꂼ��A
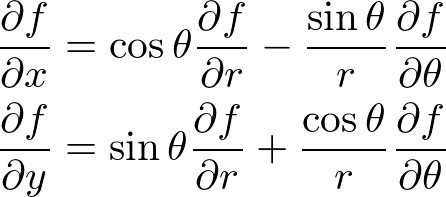
����l�ȏd�͏ꒆ�ɂ����鎿�_�̗͊w�I�G�l���M�[��
�S�����̎����g���āA�͊w�I�G�l���M�[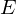 �����Ԃɂ�炸���A�܂�
�����Ԃɂ�炸���A�܂�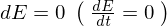 �ł��邱�Ƃ������܂��B
�ł��邱�Ƃ������܂��B
���Ȃ݂ɔ����̕\�L�̎d���͍��܂ł�����Ƃ���ł����A���ԂŔ�������ꍇ��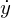 �ȂǂƂ��������������܂��B�Ӗ��I�ɂ�
�ȂǂƂ��������������܂��B�Ӗ��I�ɂ�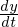 �ƑS�������ł��B�Ăѕ��̓h�b�g�Ƃ����܂��̂�
�ƑS�������ł��B�Ăѕ��̓h�b�g�Ƃ����܂��̂�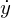 �̓��C�̃����h�b�g�ȂǂƂ������肵�܂��B
�̓��C�̃����h�b�g�ȂǂƂ������肵�܂��B
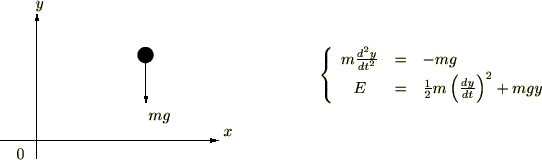
�͊w�I�G�l���M�[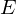 �̎��ɂ͕ϐ���
�̎��ɂ͕ϐ���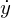 ��
��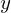 �̓�ɂȂ��Ă���̂�
�̓�ɂȂ��Ă���̂�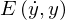 �ƕ\���܂��B
�ƕ\���܂��B
����ɑ��đS�����̎���K�p����ƁA
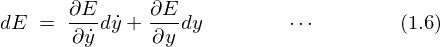
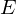 �̎������ꂼ��
�̎������ꂼ��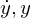 �ŕΔ������܂��B
�ŕΔ������܂��B
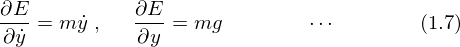
(1.6)����(1.7)�������܂��B
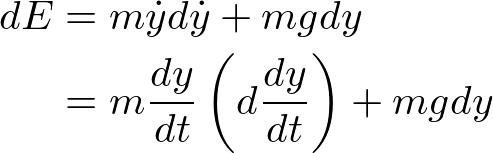
���̎����X�J���[�{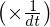 ���܂��B
���܂��B
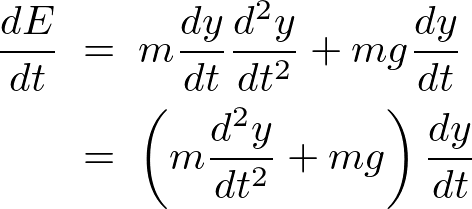
������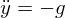 ���
���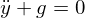
����ɂ��A
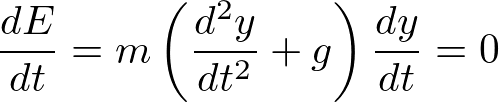
����āg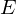 �h�͎��Ԃɂ�炸���ł���Ƃ������Ƃ��킩��܂��B
�h�͎��Ԃɂ�炸���ł���Ƃ������Ƃ��킩��܂��B
�S�����֘A�y�[�W
- ����
- ���̃Z�N�V�����ł͓����̊�{�I�ȍl�����Ƃ��̌v�Z���@�ɂ��čl�@���Ă����܂��B
- �������̔���
- �����ϕ��w�ɂ����ďd�v�ȊT�O�ł��鍇�����̊T�O�Ƃ��̔������@�Ɋւ��čl�@���Ă����܂��B
- �ΐ������@
- �ΐ������@�Ƃ͗��ӂ̑ΐ����Ƃ邱�Ƃ��疼�Â���ꂽ�����@�ł���A���̔������s���ꍇ�A�������̔��������s����ۂɗp����ꂽ�A�����Ƃ����l�������d�v�ɂȂ�܂��B
- ����
- �����ϕ��w�|�u���b�N�V���[���Y�Δ��������������߂̕Δ����Ɋւ��čl�@���Ă����܂��B1�̎��̒���2�̕ϐ��������Ă��邠����ɑ��Ă̔���h�_�@�ɂ��čl�@���Ă����܂��B
- ��ϐ����̐ϕ�
- ���T�C�g�͂��̃u���b�N�V���[���Y�Δ����������̓��o�ƒ낾���ł͂Ȃ����������߂̏������w����J�ɉ�������T�C�g�ɂȂ�܂��B���̃`���v�^�[�ł͊�{�ƂȂ镪��ɂȂ�����ϕ��Ɋւ��ĊȒP�ɐ������Ă����܂��B
- �u���ϕ�
- �Ԑ��F�L�̐ϕ��Ƃ����͎̂�ɐϕ��̌������g����悤�ɕό`������Ƃ����s�ׂ����ɏd�v�ɂȂ��Ă��܂��B���̃`���v�^�[�ł͂��̒n�Ԑ��ϕ��ɂ��Ċ����ɐ������Ă����܂��B
- �����ϕ�
- ���T�C�g�͂��̃u���b�N�V���[���Y�Δ����������̓��o�ƒ낾���ł͂Ȃ����������߂̏������w����J�ɉ�������T�C�g�ɂȂ�܂��B���̃`���v�^�[�ł͊�{�ƂȂ镪��ɂȂ�����ϕ��Ɋւ��ĊȒP�ɐ������Ă����܂��B
- �K�E�X�ϕ�
- ���T�C�g�͂��̃u���b�N�V���[���Y�Δ����������̓��o�ƒ낾���ł͂Ȃ����������߂̏������w����J�ɉ�������T�C�g�ɂȂ�܂��B���̃`���v�^�[�ł͊�{�ƂȂ镪��ɂȂ�����ϕ��Ɋւ��ĊȒP�ɐ������Ă����܂��B


























