�u���ϕ�
�y���̕ϐ��ϊ��z
�ϕ��̌v�Z�Ƃ����͎̂�ɐϕ��̌������g����悤�ɕό`������Ƃ����s�ׂ����ɏd�v�ɂȂ��Ă��܂��B
�Ⴆ�Ύ��̂悤�Ȍ`�̐ϕ������s����ɂ͂ǂ�����悢�����l���܂��B
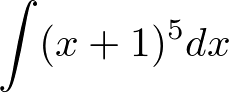
�������������̂̏ꍇ�A�ق��̂���ϐ��Œu��������i�u���j�Ƃ�����Ƃ����܂��B
��L�̖��ł͂܂����ʂ̒��� �ɒ��ڂ��Ă��������
�ɒ��ڂ��Ă��������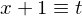 �Ƃ����܂��傤�B
�Ƃ����܂��傤�B
����� ��������ƁA
��������ƁA
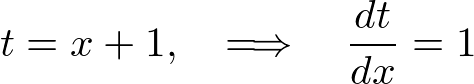
����ɂ��A
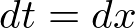
�ƂȂ�̂ł��������̎��ɑ������A
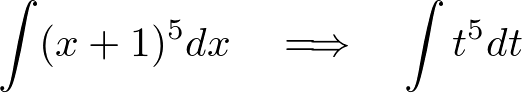
�ƂȂ�܂��B
����ʂɐϕ����A���ɖ߂��A
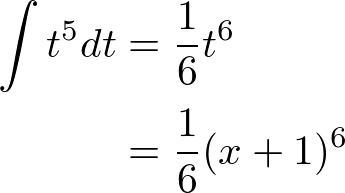
�ƂȂ�܂��B
�y���1�z
���̖���u���ϕ���p���ĉ����Ă݂܂��傤�B
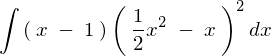
�܂��J�b�R�̒��̎������̂悤�ɂ��ƒu���Ă���� �Ŕ������܂��B
�Ŕ������܂��B
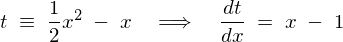
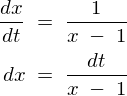
�Ƃ��Ă�������Ƃ̎��ɑ�����܂��B
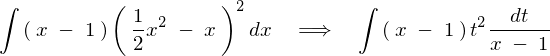
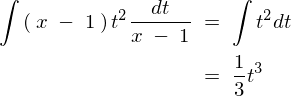
 �����ɖ߂��A
�����ɖ߂��A
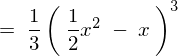
��莟�̂悤�ɋ��܂�܂��B
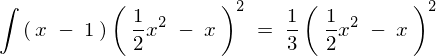
�y���2�z
���̖��������Ă݂܂��傤�B
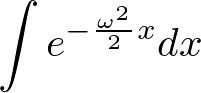
�w�����̏搔�������قǂƓ����悤�� �ɒu�����܂��B
�ɒu�����܂��B
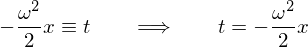
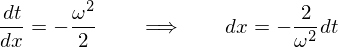
������܂��B
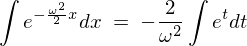
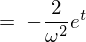
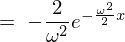
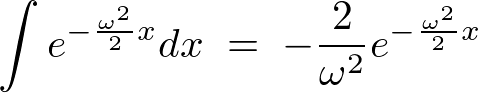
�O�p�����g�����u���ϕ�
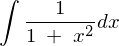
�܂� �����̂悤�ɕϐ��ϊ����܂��B
�����̂悤�ɕϐ��ϊ����܂��B
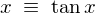
 �Ŕ������܂����^���W�F���g�́A
�Ŕ������܂����^���W�F���g�́A
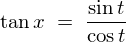
�ƕ\����̂ł�������̔��������A
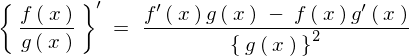
�ɓ��Ă͂߂Čv�Z���Ă����ƁA
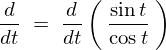
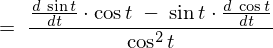
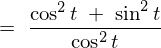
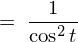
�����莟�̂悤�ɋ��܂�܂��B
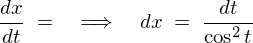
�����ŎO�p���̌���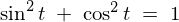 �̎���ό`���Ă݂�ƁA
�̎���ό`���Ă݂�ƁA
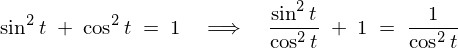
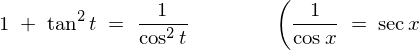
�ƂȂ�̂ł������莮�ɓ��Ă͂߂Ă����܂��B
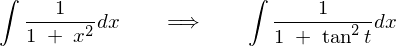
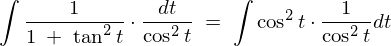
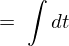
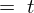
�t�ʑ��藝�ɂ��,
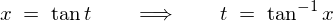
�ƂȂ�̂Ō��ʂ͈ȉ��̂悤�ɂȂ�܂��B
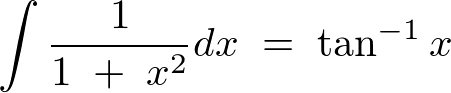
���̑��A�O�p�����g�����u���ϕ��̗�
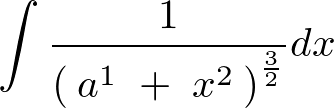
���x����قǂƓ����� ��
��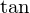 �Œu�����܂��������ł�����ƍH�v���Ď��̂悤�ɒu���܂��傤�B
�Œu�����܂��������ł�����ƍH�v���Ď��̂悤�ɒu���܂��傤�B
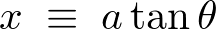
�����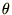 �Ŕ������܂��B
�Ŕ������܂��B
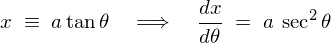
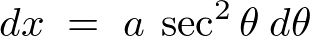
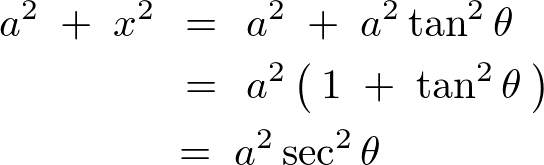
�ƂȂ�̂ł����������Ă����܂��B
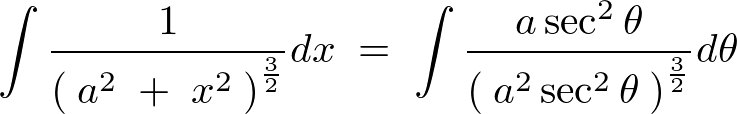
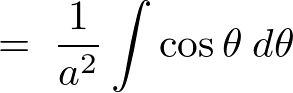
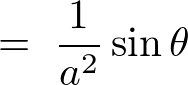
����Ɏ��̂悤�ɕϊ�����ό`���܂��B
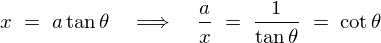
���A
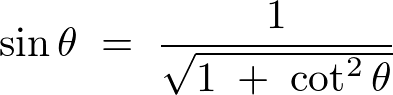
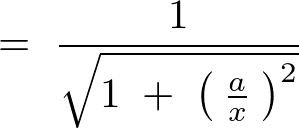
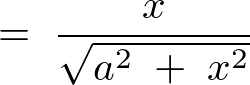
����Ď��̂悤�ɂȂ�܂��B
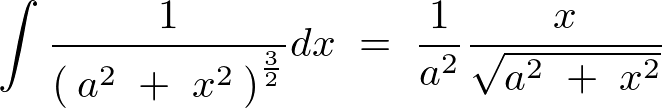
�u���ϕ��֘A�y�[�W
- ����
- ���̃Z�N�V�����ł͓����̊�{�I�ȍl�����Ƃ��̌v�Z���@�ɂ��čl�@���Ă����܂��B
- �������̔���
- �����ϕ��w�ɂ����ďd�v�ȊT�O�ł��鍇�����̊T�O�Ƃ��̔������@�Ɋւ��čl�@���Ă����܂��B
- �ΐ������@
- �ΐ������@�Ƃ͗��ӂ̑ΐ����Ƃ邱�Ƃ��疼�Â���ꂽ�����@�ł���A���̔������s���ꍇ�A�������̔��������s����ۂɗp����ꂽ�A�����Ƃ����l�������d�v�ɂȂ�܂��B
- ����
- �����ϕ��w�|�u���b�N�V���[���Y�Δ��������������߂̕Δ����Ɋւ��čl�@���Ă����܂��B1�̎��̒���2�̕ϐ��������Ă��邠����ɑ��Ă̔���h�_�@�ɂ��čl�@���Ă����܂��B
- �S����
- �S�����Ƃ͂��ׂĂ̕ϐ�������ʓ��������Ƃ��̈ꎟ�ߎ��ł̊��̕ω��ʂ�\���܂��B���̃Z�N�V�����ł͑S�����ɂ����邻�̍l�����Ƌ�̓I�Ȍv�Z���@�ɂ��čl�@���Ă����܂��B
- ��ϐ����̐ϕ�
- ���T�C�g�͂��̃u���b�N�V���[���Y�Δ����������̓��o�ƒ낾���ł͂Ȃ����������߂̏������w����J�ɉ�������T�C�g�ɂȂ�܂��B���̃`���v�^�[�ł͊�{�ƂȂ镪��ɂȂ�����ϕ��Ɋւ��ĊȒP�ɐ������Ă����܂��B
- �����ϕ�
- ���T�C�g�͂��̃u���b�N�V���[���Y�Δ����������̓��o�ƒ낾���ł͂Ȃ����������߂̏������w����J�ɉ�������T�C�g�ɂȂ�܂��B���̃`���v�^�[�ł͊�{�ƂȂ镪��ɂȂ�����ϕ��Ɋւ��ĊȒP�ɐ������Ă����܂��B
- �K�E�X�ϕ�
- ���T�C�g�͂��̃u���b�N�V���[���Y�Δ����������̓��o�ƒ낾���ł͂Ȃ����������߂̏������w����J�ɉ�������T�C�g�ɂȂ�܂��B���̃`���v�^�[�ł͊�{�ƂȂ镪��ɂȂ�����ϕ��Ɋւ��ĊȒP�ɐ������Ă����܂��B


























