����
2�̕ϐ����̔���
�P�̎��̒��ɂQ�̕ϐ�������ꍇ�̊�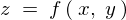 ���l���Ă݂܂��傤�B
���l���Ă݂܂��傤�B
�ϐ��͂Q����̂ŁA���̂Ƃ��̔����̎d���ɂ͎��̂Q��ނ���܂��B
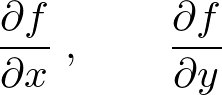
�����Δ����A�܂��͕Γ����Ƃ����A�g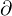 �h�͕���ɂ���ϐ��ŕΔ�������Ƃ����Ӗ��̋L���ł��B
�h�͕���ɂ���ϐ��ŕΔ�������Ƃ����Ӗ��̋L���ł��B
��ʓI�ɂ́g���E���h�h�ȂǂƂ����Ăѕ������܂��B
�v�Z�@�͂Ƃ��ɓ���l����܂ł��Ȃ��A �ŕΔ�������Ƃ���
�ŕΔ�������Ƃ��� �ȊO�̕ϐ��͒萔���Ƃ��ĕ��ʂɔ�������悢�����ł��B
�ȊO�̕ϐ��͒萔���Ƃ��ĕ��ʂɔ�������悢�����ł��B
���Ƃ��Ύ��̂悤�ȂQ�ϐ����ɂ��āA ��
��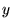 �̂��ꂼ��ɕΔ������s���Ă݂܂��傤�B
�̂��ꂼ��ɕΔ������s���Ă݂܂��傤�B
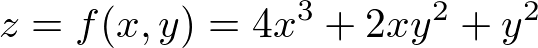
 �ɂ��Ă̕Δ����́A
�ɂ��Ă̕Δ����́A
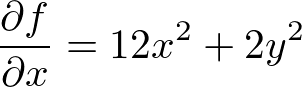
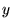 �ɂ��ẮA
�ɂ��ẮA
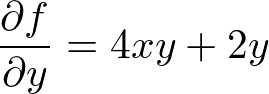
�ƂȂ�܂��B
�y���z
���Ɏ����R�ϐ����ɂ��Ă��ꂼ��̕ϐ��Ɋւ��Ă̕Δ������s���Ă݂܂��傤�B
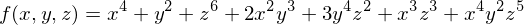
�y�����z
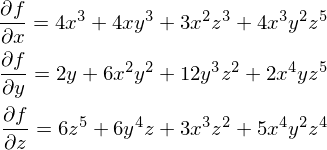
���K�̕Γ���
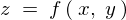 ���P��Δ�������ƁA�Q�ʂ�̌��ʂ��o�邱�Ƃ����܂����B
���P��Δ�������ƁA�Q�ʂ�̌��ʂ��o�邱�Ƃ����܂����B
���͂Q��ځA����ɂ͂���ȏ�̕Δ������J��Ԃ��Ă������ꍇ�A�ǂ��������ʂ��o�邩���l�@���Ă݂܂��傤�B
��قǂ�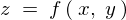 ���Q��Δ�������ƁA
���Q��Δ�������ƁA
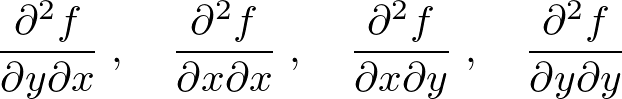
���̂S�ʂ肪���邱�Ƃ��킩��Ǝv���܂��B
����ɂR��ڂ̔���������W�ʂ�A�܂�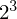 �̌��ʂ��o�܂��B
�̌��ʂ��o�܂��B
�܂��A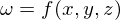 �̂R�ϐ����ɑ��ĂQ��̕Δ���������A���̂悤�Ȍ��ʁA
�̂R�ϐ����ɑ��ĂQ��̕Δ���������A���̂悤�Ȍ��ʁA
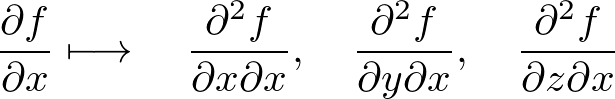
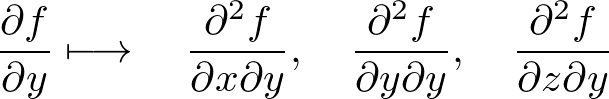
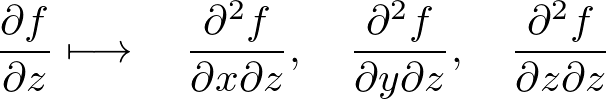
�Ƃ����A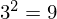 �ʂ�̌��ʂ�����Ă���Ƃ������Ƃ��킩��Ǝv���܂��B
�ʂ�̌��ʂ�����Ă���Ƃ������Ƃ��킩��Ǝv���܂��B
�܂��A����ɂR��ڂ̔������s����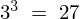 �ʂ�̌��ʂ��o�Ă��܂��B
�ʂ�̌��ʂ��o�Ă��܂��B
���ۂ�2�K�Γ����̌v�Z���s���Ă݂܂��傤�B
�y���z
����2�ϐ�����2�K�Γ��������߂Ă݂܂��傤�B
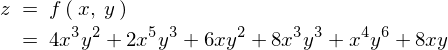
�y�����z
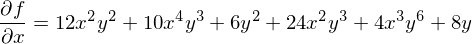
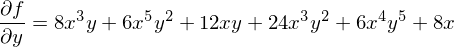
�Ȃ̂ŁA���͂��ꂼ�������ɔ������Ă����܂��B
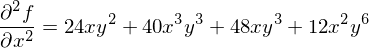
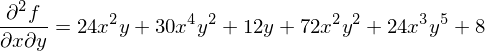
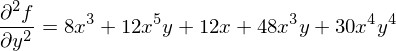
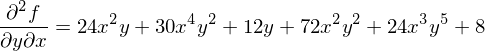
�C�Â���Ă���悤��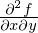 ��
��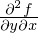 �͌��ʂ������ł��B
�͌��ʂ������ł��B
����͋��R�Ȃǂł͂Ȃ��������鏇�ԂɊW�Ȃ����ʂ������ɂȂ�Ƃ������Ƃł��B
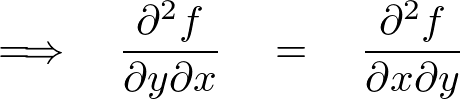
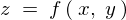 ������ł��Δ����\�Ȃ�ΕΔ������鏇���͊W���Ȃ�
������ł��Δ����\�Ȃ�ΕΔ������鏇���͊W���Ȃ�
�������L�����Δ������o���Ȃ��Ƃ��͒��ӂ��Ȃ���Ȃ�܂���B
�������̕Γ���
 ��
��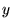 �̂Q�̕ϐ���������ɂ����āA�ϐ�
�̂Q�̕ϐ���������ɂ����āA�ϐ� ��
��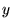 ������ɂق��̕ϐ�
������ɂق��̕ϐ�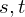 �̊��A
�̊��A
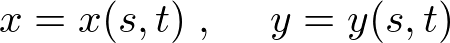
�ł���Ƃ��܂��B�܂�A
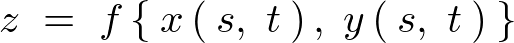
�Ƃ�����������Ƃ��A
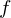 �����ꂼ��
�����ꂼ�� ��
�� �ɂ���ĕΔ���������ƁA
�ɂ���ĕΔ���������ƁA
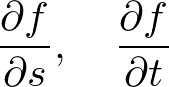
�ƂȂ�܂����A���̂Q�̕Δ��������s����ɂ�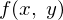 ��
�� ��
��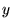 ��
��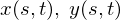 �������āA
�������āA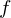 �����ׂ�
�����ׂ� ��
�� �ŏ��������Ă���v�Z����Ƃ������@���Ƃ�܂��B
�ŏ��������Ă���v�Z����Ƃ������@���Ƃ�܂��B
���̂Ƃ��A
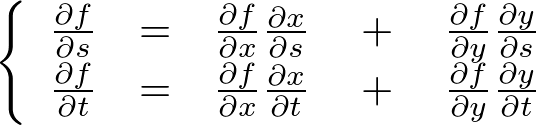
�ƂȂ�܂��B
���ۂɖ��������Ă݂܂��傤�B
�y���z
����Q�ϐ���
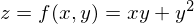
���������Ƃ��܂��B
���̕ϐ�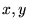 �͂���Ɏ��̂悤�ȑ��ϐ��ɂ���ĕ\�����Ƃ��܂��B
�͂���Ɏ��̂悤�ȑ��ϐ��ɂ���ĕ\�����Ƃ��܂��B
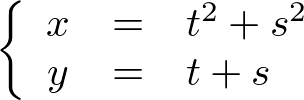
�Q�ϐ���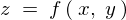 �ɑ���Δ����A
�ɑ���Δ����A
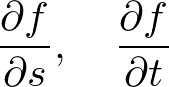
���Ă݂܂��傤�B
�y�����z
�܂� �ɂ��āA�\������Ă��邻�ꂼ��̕Δ��������s����ƁA
�ɂ��āA�\������Ă��邻�ꂼ��̕Δ��������s����ƁA
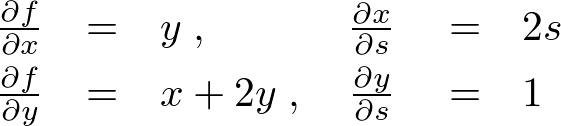
�ƂȂ�̂ŁA�������
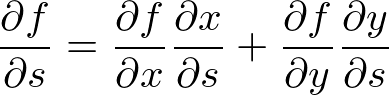
�̉E�ӂɑ������A
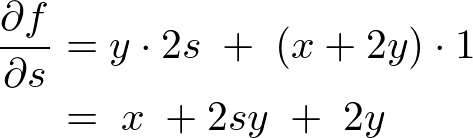
���x�� �ɂ��Ă������悤�ɁA
�ɂ��Ă������悤�ɁA
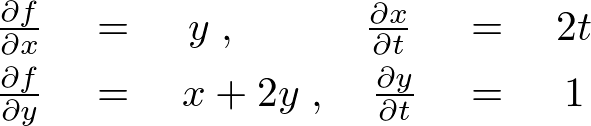
�ƂȂ�܂��B
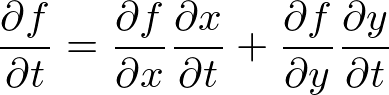
�̉E�ӂɑ������A
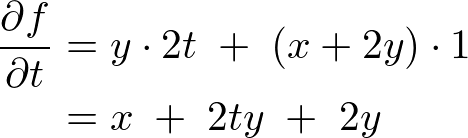
�ƂȂ�܂��B
���
�����ŏ�L�̎����g���āA
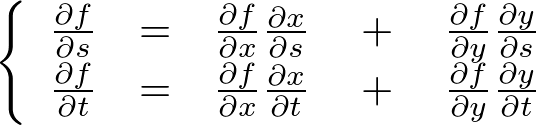
�̎�����̓I�ɍl�@���Ă݂܂��傤�B
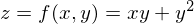 �̎���
�̎��� �ŕΔ�������ƁA
�ŕΔ�������ƁA
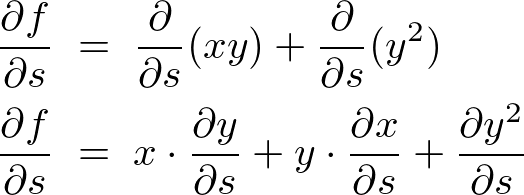
�����Ń��[�v�����܂��B
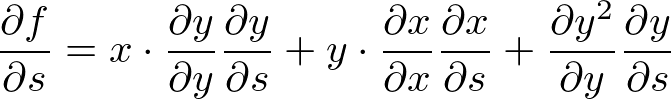
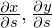 �ɒ��ڂ��āA
�ɒ��ڂ��āA
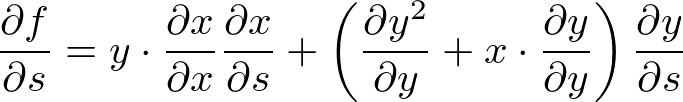
����ɉE�ӂɑ��Ĕ����̋t���Z���{���A
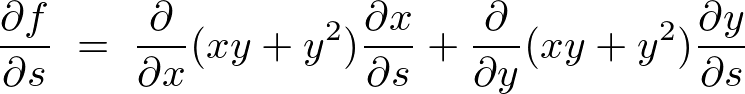
���ʂ̒��̎�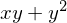 �́A
�́A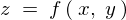 ���Ƃ������Ƃ��킩��܂��B
���Ƃ������Ƃ��킩��܂��B
�����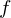 �Ə��������A
�Ə��������A
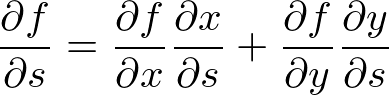
�ƂȂ�܂��B
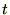 �ɑ��Ă��������ʂ��łĂ��܂��B
�ɑ��Ă��������ʂ��łĂ��܂��B
�Δ����֘A�y�[�W
- ����
- ���̃Z�N�V�����ł͓����̊�{�I�ȍl�����Ƃ��̌v�Z���@�ɂ��čl�@���Ă����܂��B
- �������̔���
- �����ϕ��w�ɂ����ďd�v�ȊT�O�ł��鍇�����̊T�O�Ƃ��̔������@�Ɋւ��čl�@���Ă����܂��B
- �ΐ������@
- �ΐ������@�Ƃ͗��ӂ̑ΐ����Ƃ邱�Ƃ��疼�Â���ꂽ�����@�ł���A���̔������s���ꍇ�A�������̔��������s����ۂɗp����ꂽ�A�����Ƃ����l�������d�v�ɂȂ�܂��B
- �S����
- �S�����Ƃ͂��ׂĂ̕ϐ�������ʓ��������Ƃ��̈ꎟ�ߎ��ł̊��̕ω��ʂ�\���܂��B���̃Z�N�V�����ł͑S�����ɂ����邻�̍l�����Ƌ�̓I�Ȍv�Z���@�ɂ��čl�@���Ă����܂��B
- ��ϐ����̐ϕ�
- ���T�C�g�͂��̃u���b�N�V���[���Y�Δ����������̓��o�ƒ낾���ł͂Ȃ����������߂̏������w����J�ɉ�������T�C�g�ɂȂ�܂��B���̃`���v�^�[�ł͊�{�ƂȂ镪��ɂȂ�����ϕ��Ɋւ��ĊȒP�ɐ������Ă����܂��B
- �u���ϕ�
- �Ԑ��F�L�̐ϕ��Ƃ����͎̂�ɐϕ��̌������g����悤�ɕό`������Ƃ����s�ׂ����ɏd�v�ɂȂ��Ă��܂��B���̃`���v�^�[�ł͂��̒n�Ԑ��ϕ��ɂ��Ċ����ɐ������Ă����܂��B
- �����ϕ�
- ���T�C�g�͂��̃u���b�N�V���[���Y�Δ����������̓��o�ƒ낾���ł͂Ȃ����������߂̏������w����J�ɉ�������T�C�g�ɂȂ�܂��B���̃`���v�^�[�ł͊�{�ƂȂ镪��ɂȂ�����ϕ��Ɋւ��ĊȒP�ɐ������Ă����܂��B
- �K�E�X�ϕ�
- ���T�C�g�͂��̃u���b�N�V���[���Y�Δ����������̓��o�ƒ낾���ł͂Ȃ����������߂̏������w����J�ɉ�������T�C�g�ɂȂ�܂��B���̃`���v�^�[�ł͊�{�ƂȂ镪��ɂȂ�����ϕ��Ɋւ��ĊȒP�ɐ������Ă����܂��B


























