����
�����̒�`�Ƃ��Ă͎��̂悤�ɂȂ�܂��B
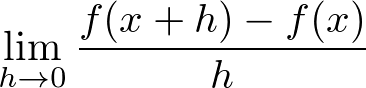
��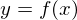 �̓����ƌĂт܂��B
�̓����ƌĂт܂��B
�\�L�̎d���́A
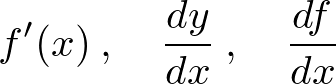
�ȂǂƏ����܂��B
�܂��͊�{�I�Ȍv�Z����s���܂��傤�B
���̂悤�Ȋ����l���܂��B
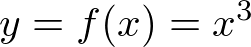
���̎���L�́A
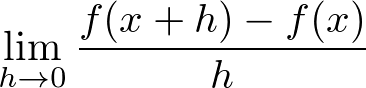
���g���Čv�Z����ƁA
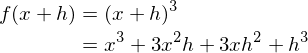
�����������A
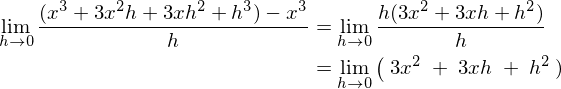
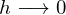 �Ȃ̂ŁA
�Ȃ̂ŁA
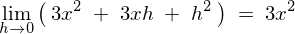
�ƂȂ�܂��B
��v�Ȕ�������
�ȉ��Ɏ��������̂͏d�v�ł��̂ł�������o����悤�ɂ��܂��傤�B
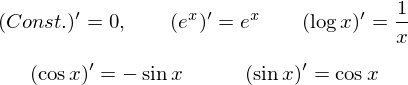
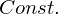 �Ƃ����̂͒萔�ł��B
�Ƃ����̂͒萔�ł��B
���������猋�ʂ�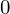 �ɂȂ�܂��B
�ɂȂ�܂��B
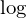 �Ƃ����̂͑ΐ����ł��B����
�Ƃ����̂͑ΐ����ł��B����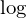 �͂��̕ϐ�
�͂��̕ϐ� �Ŕ��������
�Ŕ��������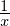 �Ƃ������ʂɂȂ�܂��B
�Ƃ������ʂɂȂ�܂��B
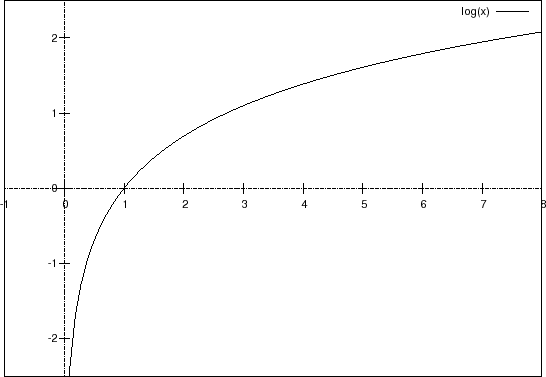
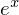 �͎w�����ł���A�Ăѕ��͂����̃C�[���A�łȂ���C�N�X�|�[�l���V�����Ȃǂƌ������肵�܂��B
�͎w�����ł���A�Ăѕ��͂����̃C�[���A�łȂ���C�N�X�|�[�l���V�����Ȃǂƌ������肵�܂��B
����͔������Ă��ϕ����Ă��������ʂ��o�Ă��܂��B�������搔�����ɂ����ȕϐ�����������Ă���ꍇ�͒��ӂ��K�v�ł��B
���Ȃ݂�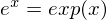 �Ƃ������\����������܂��B
�Ƃ������\����������܂��B
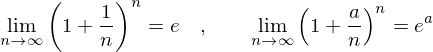
�O���t�͈ȉ��̂悤�ɂȂ�܂��B
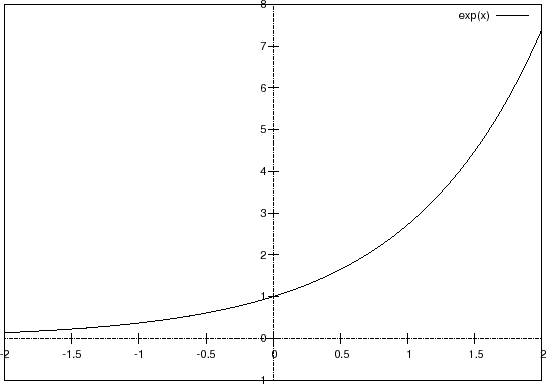
�O���t����킩��悤��
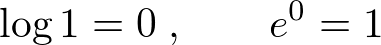
�ƂȂ�܂��B
�ς̔���
��̊����ς̌`�ɂȂ��Ă���Ƃ��̔����͎��̂悤�ɂȂ�܂��B
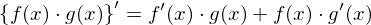
���̌����𗘗p���A���Ɏ������̔���������Ă݂܂��傤�B
���̌����𗘗p���A���Ɏ������̔���������Ă݂܂��傤�B
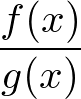
���̎��́A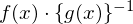 �ƕ\���邩�Ǝv���܂��B
�ƕ\���邩�Ǝv���܂��B
��L�̌������g���ƁA
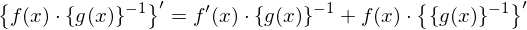
�ƂȂ�܂��B��ʓI�ɂ�
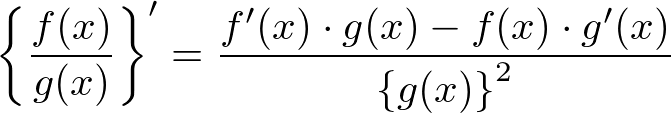
�ȂǂƏ����܂��B
�y���z
���̊���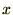 �Ŕ������Ă݂܂��傤�B
�Ŕ������Ă݂܂��傤�B

�y�����z
�����ɂ��Ă͂߂Ă��ꂼ��v�Z���Ă����܂��B
���(1)
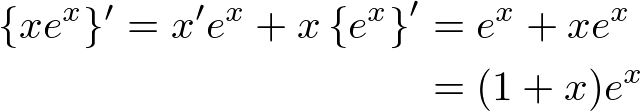
���(2)
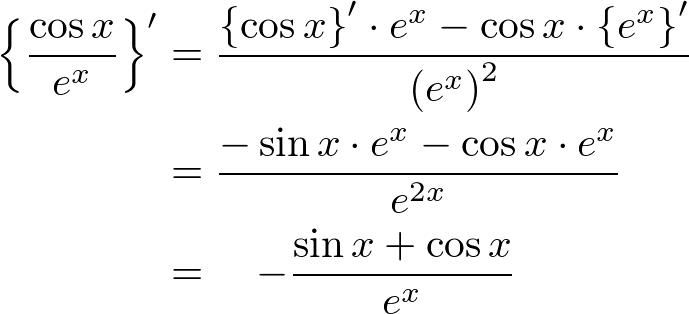
�����֘A�y�[�W
- �������̔���
- �����ϕ��w�ɂ����ďd�v�ȊT�O�ł��鍇�����̊T�O�Ƃ��̔������@�Ɋւ��čl�@���Ă����܂��B
- �ΐ������@
- �ΐ������@�Ƃ͗��ӂ̑ΐ����Ƃ邱�Ƃ��疼�Â���ꂽ�����@�ł���A���̔������s���ꍇ�A�������̔��������s����ۂɗp����ꂽ�A�����Ƃ����l�������d�v�ɂȂ�܂��B
- ����
- �����ϕ��w�|�u���b�N�V���[���Y�Δ��������������߂̕Δ����Ɋւ��čl�@���Ă����܂��B1�̎��̒���2�̕ϐ��������Ă��邠����ɑ��Ă̔���h�_�@�ɂ��čl�@���Ă����܂��B
- �S����
- �S�����Ƃ͂��ׂĂ̕ϐ�������ʓ��������Ƃ��̈ꎟ�ߎ��ł̊��̕ω��ʂ�\���܂��B���̃Z�N�V�����ł͑S�����ɂ����邻�̍l�����Ƌ�̓I�Ȍv�Z���@�ɂ��čl�@���Ă����܂��B
- ��ϐ����̐ϕ�
- ���T�C�g�͂��̃u���b�N�V���[���Y�Δ����������̓��o�ƒ낾���ł͂Ȃ����������߂̏������w����J�ɉ�������T�C�g�ɂȂ�܂��B���̃`���v�^�[�ł͊�{�ƂȂ镪��ɂȂ�����ϕ��Ɋւ��ĊȒP�ɐ������Ă����܂��B
- �u���ϕ�
- �Ԑ��F�L�̐ϕ��Ƃ����͎̂�ɐϕ��̌������g����悤�ɕό`������Ƃ����s�ׂ����ɏd�v�ɂȂ��Ă��܂��B���̃`���v�^�[�ł͂��̒n�Ԑ��ϕ��ɂ��Ċ����ɐ������Ă����܂��B
- �����ϕ�
- ���T�C�g�͂��̃u���b�N�V���[���Y�Δ����������̓��o�ƒ낾���ł͂Ȃ����������߂̏������w����J�ɉ�������T�C�g�ɂȂ�܂��B���̃`���v�^�[�ł͊�{�ƂȂ镪��ɂȂ�����ϕ��Ɋւ��ĊȒP�ɐ������Ă����܂��B
- �K�E�X�ϕ�
- ���T�C�g�͂��̃u���b�N�V���[���Y�Δ����������̓��o�ƒ낾���ł͂Ȃ����������߂̏������w����J�ɉ�������T�C�g�ɂȂ�܂��B���̃`���v�^�[�ł͊�{�ƂȂ镪��ɂȂ�����ϕ��Ɋւ��ĊȒP�ɐ������Ă����܂��B


























