�m�����x���ƕϐ��ϊ�
�ϐ��ϊ��ɂ���č��ꂽ�m�����x�������߂���@�ɂ��ẮA�m���ϐ��̕ϊ��ɂ���ċ��߂邽�߂̌���������A���̌�����p���邱�ƂŖړI�̊m�����x�������߂邱�Ƃ��ł���B
�m�����x
�m���ϐ���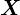 �A�����l�i�����j��
�A�����l�i�����j�� �ŕ\�����邱�Ƃɂ���B
�ŕ\�����邱�Ƃɂ���B
���ɂQ�̎����Ƃ���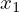 �A
�A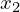 ��
��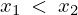 ���Ƃ���ƁA
���Ƃ���ƁA
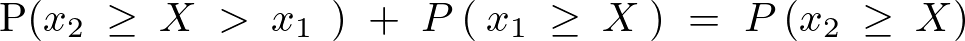
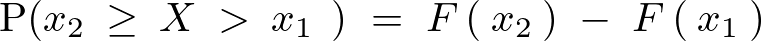
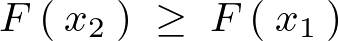
������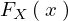 ��
��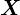 �̗ݐϕ��z���icumulative distribution function�j�Ƃ��āA���̗ݐϕ��z�������̂悤�ɒ�`���邱�Ƃɂ���B
�̗ݐϕ��z���icumulative distribution function�j�Ƃ��āA���̗ݐϕ��z�������̂悤�ɒ�`���邱�Ƃɂ���B
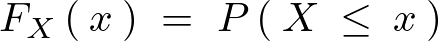
�����܂ŗݐϕ��z��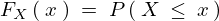 �ƂȂ�ꍇ�̊m���Ȃ̂ō��x��
�ƂȂ�ꍇ�̊m���Ȃ̂ō��x��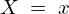 �ƂȂ鎟�̂悤��
�ƂȂ鎟�̂悤�� �̊m���A
�̊m���A
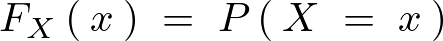
���l���āi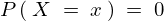 �ƂȂ�Ȃ��j����𖧓x���Ƃ���B
�ƂȂ�Ȃ��j����𖧓x���Ƃ���B
�����S��ɂ킽���čl����A
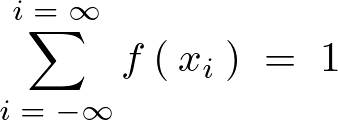
���z���Ɛ�قǂ̖��x���Ƃ̊W�͈ȉ��̂悤�ɂȂ�B
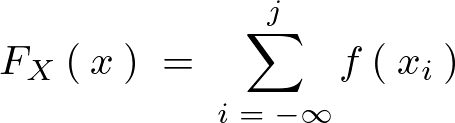
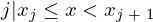
�m�����x��
�A���m�����z�ɂ����Ĉȉ��̂悤�Ȋm�����x��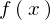 �����݂���B
�����݂���B
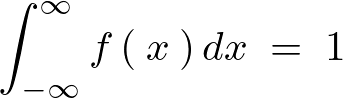
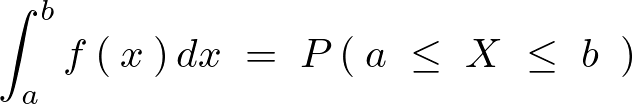
�����ł���ɗݐϕ��z����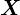 ��
�� �Ƃ������l�ȉ��̒l���Ƃ�m���ƍl����ƁA
�Ƃ������l�ȉ��̒l���Ƃ�m���ƍl����ƁA
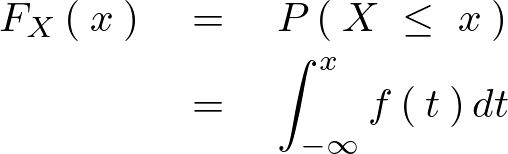
�m�����x��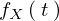 ��
��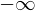 ����
���� �Őϕ��������̂�
�Őϕ��������̂�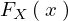 �Ƃ������z���ɂȂ�B
�Ƃ������z���ɂȂ�B
�����ϕ��w�̊�{�藝�ɂ��ȉ��A
| �m�����x�� | �ݐϕ��z��������������� |
|---|---|
| �ݐϕ��z�� | �m�����x����ϕ��������� |
�����藧�B
�ȏ�ɂ��A���^�m���ϐ��̗ݐϕ��z���͊m�����x�������݂���ꍇ�A �̕��z��
�̕��z��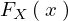 �͈ȉ��̂悤�ɕ\�������B
�͈ȉ��̂悤�ɕ\�������B
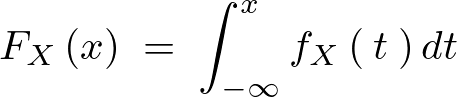
����Ɉʒu �ƂȂ�悤�ȘA����������ꍇ�ƍl���A�܂��A�����ϕ��w�̑���{�藝���A�ݐϕ��z����
�ƂȂ�悤�ȘA����������ꍇ�ƍl���A�܂��A�����ϕ��w�̑���{�藝���A�ݐϕ��z���� �Ŕ�������Ώ�L�m�����x���͈ȉ��̂悤�ɂł���B
�Ŕ�������Ώ�L�m�����x���͈ȉ��̂悤�ɂł���B
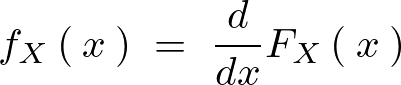
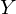 �̎��ӊm�����z��
�̎��ӊm�����z��
���̕��z�������x��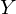 �ɂ��čl����Ɛ�قǂ�
�ɂ��čl����Ɛ�قǂ� �̕��z��
�̕��z��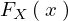 �ɂ�����l�@�P����A
�ɂ�����l�@�P����A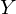 �̕��z��
�̕��z��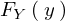 �́A
�́A
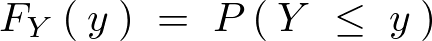
����ɂ����ł����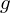 ���l���Ă�������̂悤�ɒu�����Ƃɂ���B
���l���Ă�������̂悤�ɒu�����Ƃɂ���B
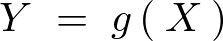
��L���Ɋւ��Ă͂��ꂼ��̕ϐ��ɑΉ�����t���A
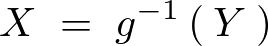
�Ȃ�t�ʑ��������݂�����̂��Ƃ�������͍l��������B
�ȏ��������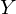 �ɂ�������ӊm�����z�����߂Ă����B
�ɂ�������ӊm�����z�����߂Ă����B
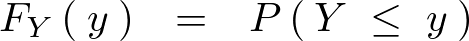
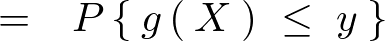
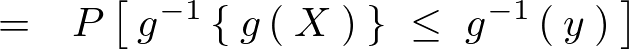
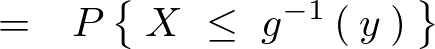
����ɂ�����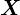 ��
�� �̗v�f�ƍl�����A
�̗v�f�ƍl�����A

����ɂ��A
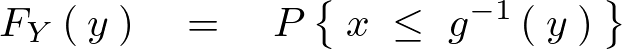
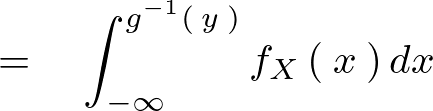
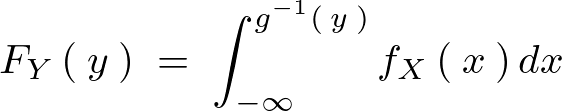
�ϐ��ϊ�
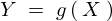 ����A
����A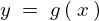 ���A
���A
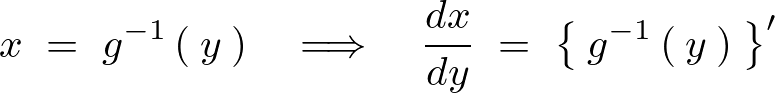
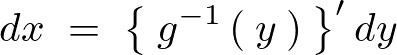
������A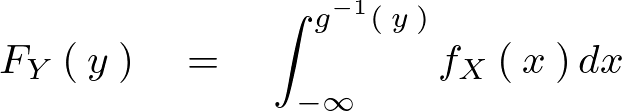
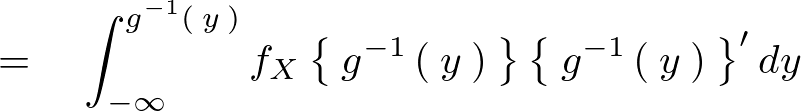
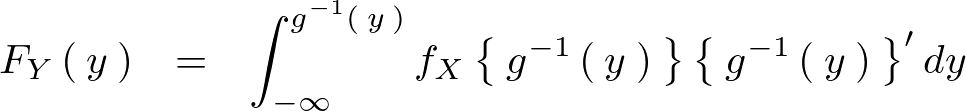
�Ƃ����悤�Ȏ��ό`�ɂ��ϕ��������܂�̂ł����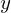 �Ŕ����i�����^�Ɂj����ƁA�܂��������v���C���ŕ\���Ă��镔�������C�v�j�b�c�\�L�ɂ���Ύ��̂悤�Ȃ�B
�Ŕ����i�����^�Ɂj����ƁA�܂��������v���C���ŕ\���Ă��镔�������C�v�j�b�c�\�L�ɂ���Ύ��̂悤�Ȃ�B
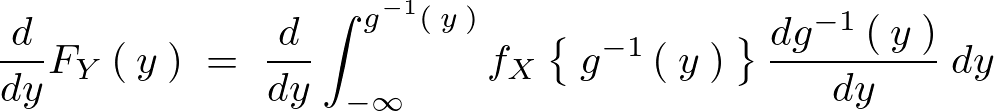
�`���炵�Ă��̂܂ܐϕ��������O���������Q�l���x�ɂ����ĉ�肭�ǂ�����������Έȉ��̂悤�Ȍv�Z�ߒ��ɂȂ�B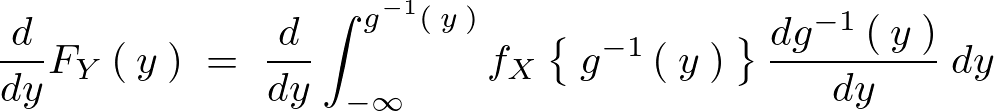
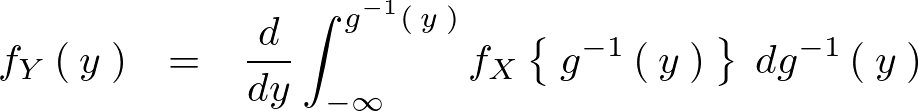
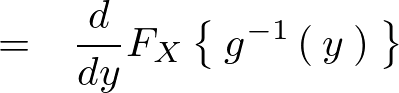
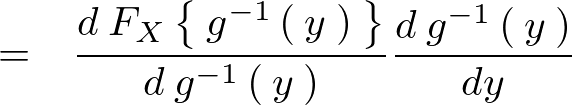
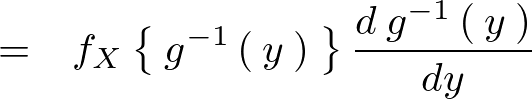
����Ċm�����x��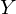 �ɂ�������ӊm�����x���͈ȉ��̂悤�ɂȂ�B
�ɂ�������ӊm�����x���͈ȉ��̂悤�ɂȂ�B
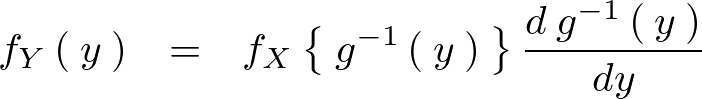
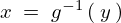 ��茳�ɖ߂��A
��茳�ɖ߂��A
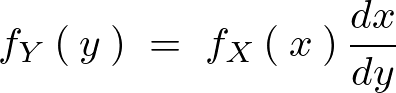
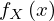 ����
����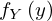 �̎��ӊm�����x���̈Ӗ�
�̎��ӊm�����x���̈Ӗ�
�㎮�ɂ��Ă�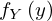 �̎��ӊm�����x�������߂�Ƃ������Ƃɂ�����
�̎��ӊm�����x�������߂�Ƃ������Ƃɂ�����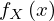 �̎��ӊm�����x�ւɑ��Ă��̍��W�n���ω��������̕������l�����邽�߂�
�̎��ӊm�����x�ւɑ��Ă��̍��W�n���ω��������̕������l�����邽�߂�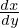 �Ƃ����̂��t������Ƃ��������Ƃ��Ӗ����Ă��邱�ƂɂȂ�A����͊m���͈͂�����ʐςłƂ炦���Ă���ƍl�����ꍇ�A���̖ʐϔ͈͂��e�X�̎��ӊm�����x�̖ʐς��Ƃ����
�Ƃ����̂��t������Ƃ��������Ƃ��Ӗ����Ă��邱�ƂɂȂ�A����͊m���͈͂�����ʐςłƂ炦���Ă���ƍl�����ꍇ�A���̖ʐϔ͈͂��e�X�̎��ӊm�����x�̖ʐς��Ƃ����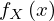 ����
����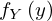 �ւ̎��Ӗ��x�֕ϊ����Ă������ꍇ�̍��W�ϊ��ɂ�����ʐϗv�f�i��ϐ��j�ϊ��̕ϊ������ƂƂ炦������炵���A����͓��h���C���̃T�e���C�g�T�C�g�i�悭�킩�銵�����[�����g�j�ł��悭�g���Ă����ϐ��ϊ����R�r�A���i���s�j�̂��Ƃɂ�����炵���B
�ւ̎��Ӗ��x�֕ϊ����Ă������ꍇ�̍��W�ϊ��ɂ�����ʐϗv�f�i��ϐ��j�ϊ��̕ϊ������ƂƂ炦������炵���A����͓��h���C���̃T�e���C�g�T�C�g�i�悭�킩�銵�����[�����g�j�ł��悭�g���Ă����ϐ��ϊ����R�r�A���i���s�j�̂��Ƃɂ�����炵���B
�������ȉ����Ђ��Q�l�ɂ��Ă��܂���
���R�r�A���ƕϐ��ϊ�
��L��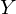 �̎��Ӗ��x��
�̎��Ӗ��x��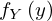 �͈�ϐ��ɂ�������Ӗ��x���ɂȂ邪���ꂪ2�ϐ��ȏ�̑��ϗʂɂȂ������̂��l����ꍇ�A���R�r�A���ɓ����镔���ɐ�Βl�����邱�Ƃ��K�v�ɂȂ�Ƃ̂��ƁB����͑Ή��i�ω��j��������W��Ԃ����W����ɍ��킹��Ƃ������Ƃ��Ӗ����Ă���炵���B
�͈�ϐ��ɂ�������Ӗ��x���ɂȂ邪���ꂪ2�ϐ��ȏ�̑��ϗʂɂȂ������̂��l����ꍇ�A���R�r�A���ɓ����镔���ɐ�Βl�����邱�Ƃ��K�v�ɂȂ�Ƃ̂��ƁB����͑Ή��i�ω��j��������W��Ԃ����W����ɍ��킹��Ƃ������Ƃ��Ӗ����Ă���炵���B
�Q�l�T�C�g
���w�̌i�F �l
�d�ϕ��̕ϐ��ϊ��̕��@�Ƃ��̗��`�ɍ��W�ϊ��̉���t���`
��قǂ���d�����Ă���悤��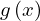 �Ƃ������͘A�������\�̋t��
�Ƃ������͘A�������\�̋t��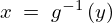 �����Ƃ��Ă���̂ł�����
�����Ƃ��Ă���̂ł����� �̊e�v�f��
�̊e�v�f��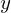 �̊e�v�f�ŕΔ����������R�r�A����
�̊e�v�f�ŕΔ����������R�r�A����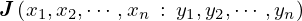 �ƒu���Ύ��̂悤�Ȋ��s�i���R�r�A���j���l�����邱�ƂɂȂ�B
�ƒu���Ύ��̂悤�Ȋ��s�i���R�r�A���j���l�����邱�ƂɂȂ�B
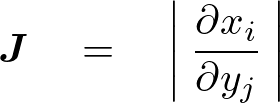

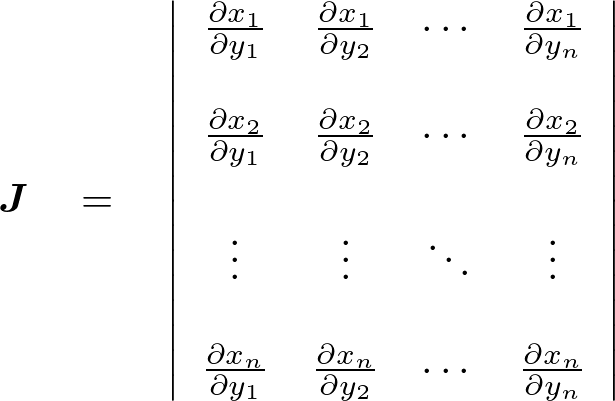
�����ŏ�L���R�r�A���ɑ��Ă͑��ϗʂɂȂ�Ƃ��̃��R�r�A���ɂ͐�Βl�����̂ŁA
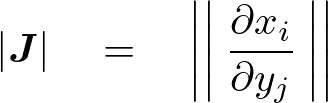
�Ƃ������\�L�ɂȂ�Ǝv������L���Ɋւ��Ă͈�ʓI�ł͂Ȃ��Ӗ��I�ɂ�₱�����̂łЂƂ܂����̂悤�ɂ������Ƃɂ���B
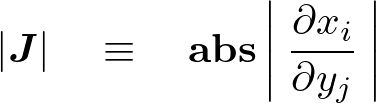
���̕\�L�Ɋւ��Ă͂����܂ł��̃T�C�g�݂̂ł́i�������g�ł킩��₷�����邽�߂́j�\���ɂȂ�̂ł��܂�Q�l�ɂ��Ȃ��悤�ɁB
�ڂ����͏�L�̏����V�������Ł@���㐔�����v�w [ �|���@���� ]���Q�Ƃ���悤�ɁB
�Ȃ̂ňȏ�ɂ��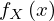 ����
����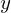 �̎��ӊm�����x�����ꍇ�A��ϐ��Ɋւ��ẮA
�̎��ӊm�����x�����ꍇ�A��ϐ��Ɋւ��ẮA
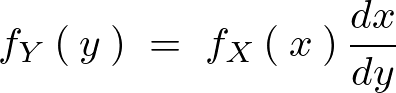
��������A���ꂪ���ϗʂ̏ꍇ�ɂȂ�ƁA
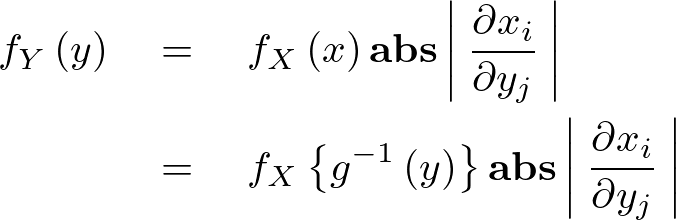
���A
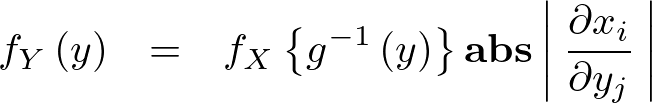
����Ɋւ���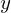 �Őϕ�����Ώd�ϕ��̕ϐ��ϊ������i�ڂ������V�������Ł@���㐔�����v�w [ �|���@���� ]���Q�Ɓj�ɂȂ邱�Ƃ��킩��B
�Őϕ�����Ώd�ϕ��̕ϐ��ϊ������i�ڂ������V�������Ł@���㐔�����v�w [ �|���@���� ]���Q�Ɓj�ɂȂ邱�Ƃ��킩��B
�������d�����邪��L�\���͂����܂œ��T�C�g�ł̎������g�ł킩��₷���悤�ɓƎ��ŕ\�����Ă��邾���Ȃ̂ł��̂ւ�̂Ƃ���͊��Ⴂ���Ȃ��悤�ɁB
�m�����x���ƕϐ��ϊ��֘A�y�[�W
- ���R�r�A���A�i�쐬�ҏW���j
- ���T�C�g�͎�ɕ����Ɋւ��鐔�w�ȂǁA���̑����ӂ��܂߂����X�������ς̃E�F�u�T�C�g�ł��B �������v�w�|���̃R���e���c�ł͑��ϗʉ�͂ɂ����ďd�v�ȍl�����ɂȂ�ϐ��ϊ��ɂ�郄�R�r�A���i���s�j�ɂ��čl�@���A�������ɂ�������W�ϊ��ł��̊w�I�ȈӖ����Ă����܂��B
- ���R�r�A���@
- ���T�C�g�͎�ɕ����Ɋւ��鐔�w�ȂǁA���̑����ӂ��܂߂����X�������ς̃E�F�u�T�C�g�ł��B �������v�w�|���̃R���e���c�ł͑��ϗʉ�͂ɂ����ďd�v�ȍl�����ɂȂ�ϐ��ϊ��ɂ�郄�R�r�A���i���s�j�ɂ��čl�@���Ă����܂��B
![[���i���i�Ɋւ��܂��ẮA�����N���쐬���ꂽ���_�ƌ����_�ŏ�ύX����Ă���ꍇ���������܂��B] [���i���i�Ɋւ��܂��ẮA�����N���쐬���ꂽ���_�ƌ����_�ŏ�ύX����Ă���ꍇ���������܂��B]](https://hbb.afl.rakuten.co.jp/hgb/038f923b.33eaf06f.11b69812.5ccdc4a9/?me_id=1213310&item_id=20073751&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F8601%2F9784780608601.jpg%3F_ex%3D300x300&s=300x300&t=picttext)
























