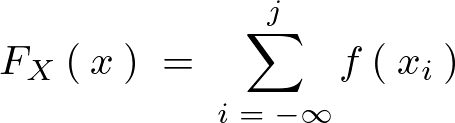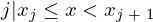前回に続き、ヤコビアンの考察に入る。
ある座標系から別の座標系へうつるとき、例えば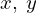 のカーテシャン座標系から別の座標系の平面極座標系r-θへの変換を考えた場合、微小面積dxdyに対するr-θの微小面積に対してどの程度のスケール変換量をスカラー倍すれば同等の面積素分になるかを考えるとき、まず、その幾何学的な関係を写像という関係性によって次のような相似関係、
のカーテシャン座標系から別の座標系の平面極座標系r-θへの変換を考えた場合、微小面積dxdyに対するr-θの微小面積に対してどの程度のスケール変換量をスカラー倍すれば同等の面積素分になるかを考えるとき、まず、その幾何学的な関係を写像という関係性によって次のような相似関係、
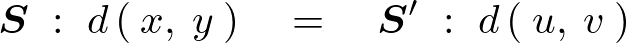
が導かれることになり、さらにこれを変形していけば
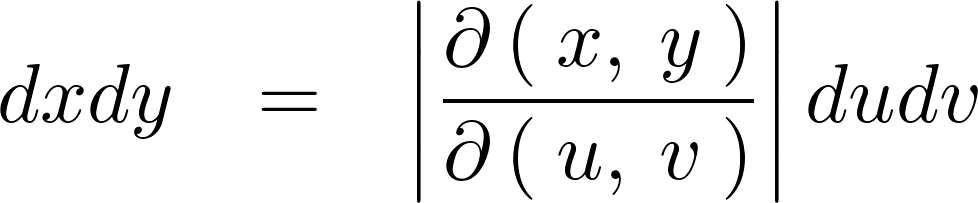
前回に続き、ヤコビアンの考察に入る。
ある座標系から別の座標系へうつるとき、例えば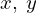 のカーテシャン座標系から別の座標系の平面極座標系r-θへの変換を考えた場合、微小面積dxdyに対するr-θの微小面積に対してどの程度のスケール変換量をスカラー倍すれば同等の面積素分になるかを考えるとき、まず、その幾何学的な関係を写像という関係性によって次のような相似関係、
のカーテシャン座標系から別の座標系の平面極座標系r-θへの変換を考えた場合、微小面積dxdyに対するr-θの微小面積に対してどの程度のスケール変換量をスカラー倍すれば同等の面積素分になるかを考えるとき、まず、その幾何学的な関係を写像という関係性によって次のような相似関係、
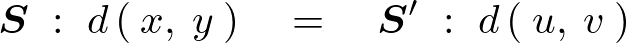
が導かれることになり、さらにこれを変形していけば
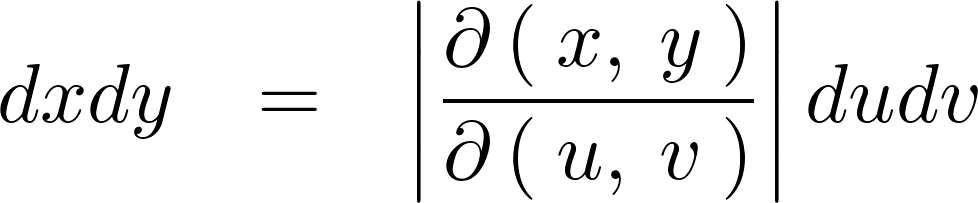



単刀直入に言うと、このエントリーは確率密度関数と変数変換コンテンツの続きではあるがよくわかる慣性モーメントの更新コンテンツも兼ねている。
ディレクトリ構造としては数理統計学の配下にあるサブカテゴリーの確率の数理の中で以下のように配置してあるエントリー(コンテンツ)になる。
数理統計学(カテゴリ)
┗確率の数理(サブカテゴリ)
┗ヤコビアン①(このページ)
┗確率密度関数と変数変換
当サイトは元々は物理専門のサイトであり物理専攻の人からからすれば微分積分、解析力学などで使われるものがなぜ数理統計学の多変量解析に?と面食らう人もいるだろうが、このヤコビアンというのは多変量解析においてよく登場し、しかも結構重要な役割をはたしている。
これに関しては順を追って解説していこうと思う。
ちなみに将来データエンジニアといったシステムエンジニアを目指している人などは多変量解析の知識を必要とされる場合があると思うが、それに対応した際にこうした部分の知識があればのちに役立つ内容になっていると思う。
このドメイン下での数学物理関連のコンテンツは基本的にドラフトコンテンツであり、今後本サイトのほうへ移す際の査読記事みたいなものを置く場合もある。
今回のコンテンツはそれにあたる。
前々から言っているようにサテライトサイトのよくわかる慣性モーメントを筆頭にして、それ以外にもサルでもわかる線形代数やよくわかるベクトル解析といったこのドメイン下のコンテンツ盗用が問題になっており、その対策としてのコンテンツ更新及びその拡充の一環になる。
もともと本職が忙しいというのも本音としてあるが今までコンテンツを拡充していなかったのは難しい理論や考え方などは除いてWebサイトへの入り口というか間口を広くしておきたかったというのがある。
例えばよくわかる慣性モーメントに関する派生知識として“慣性モーメントテンソル”などといったものがあるが、あまり数学に慣れ親しんでない人の場合その単語(テンソル)が出てきた時点である種の“客離れ(サイトに訪れてもすぐに離れる)”になる可能性もある。
こういったことを避けるために私が運営する数学物理学コンテンツはなるべく難しい内容を避けつつ簡潔かつ初等レベルで理解できることを目標としたサイト作成を心がけているといった事もその一因になっている。
つまり基本としては道具としての数学を身に付けてもらいながらその他のコンテンツ、とりわけ特亜に関するコンテンツにも興味を持ってもらうための布石となるべく作られており、その対象は一般社会人をはじめとし、中学・高校生といったまだ10代の学生さん、さらに欲を言えば小学生でも意味程度なら理解できて興味をもって見てもらえるものを目標としたコンテンツ作成を主眼においている。
しかしながら昨今のコンテンツ盗用の状況を鑑みればサイトの内容を常に更新し、ある程度の専門性を持たせながらコンテンツの量を増やしていくことが一番の対策になるというのが実情としてあり、今後もコンテンツの拡充をしながら本来のサイト作成の方向性を少し変更していかなければならない時期かなと考えている。
ということで前回、第1弾、そして第2弾として円錐の慣性モーメントを取り扱ったが、今度は第3弾としてヤコビアンを取り上げることにした。
題名としては「変数変換とヤコビアン」であるが、これはもともと数理統計学の中のコンテンツ、「多変量確立ベクトルの計算」 → 「確率密度関数と変数変換」、といった内容の続きとして考えていたコンテンツになる。
このヤコビアンというものに関しては「よくわかる慣性モーメント」の中のサブカテゴリコンテンツにも「ヤコビアン」というのがあり、これに付加コンテンツとして取り上げる予定になっている。
一般的にというかまあなんでもそうなのだが自分で理解するよりも他人に教えることのほうが難しいというのはよく言われるが、物理学における慣性モーメントの周辺知識としてわかりずらい、または他者に教えて理解してもらうのがやや困難なものとしては先ほど上げた慣性モーメントテンソル以外のものとして今回取り上げるこのヤコビアンというものになる。
道具として使うだけならば線形代数における行列式の計算ができればそれで特に問題がないものになるが、座標変換をする際の写像においてなぜヤコビ行列というものが出てくるのか、といったその根本的な考え方と説明になっている。

はいはいそれではまずヤコビアンにおける変数変換とはなんなのかから説明していきましょう。
ただし重複するがあくまでドラコンの域を出ないのでかなり粗削りで、しかも独自の考察による内容になっているのでそのへんは注意して閲覧するように。
改めて説明すると多変量解析において重要な確率分布で多変量正規分布というのがあり、これを導く際に重要なものとしてヤコビアン(関数行列式)というのがある。
変数変換における重積分の公式では以下のようになっている。
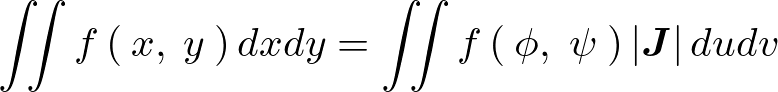
上記式の絶対値で囲まれている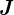 がそのヤコビアンに当たる。
がそのヤコビアンに当たる。
一般的に座標系といえば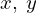 で与えられた場合通常デカルト座標系といったものを使う。
で与えられた場合通常デカルト座標系といったものを使う。
ここでその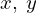 に対して新たに
に対して新たに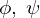 といった関数を考えてその変数を
といった関数を考えてその変数を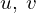 と置き、それが
と置き、それが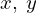 とは可逆的な関係であるとして次のような式を考えることにする。
とは可逆的な関係であるとして次のような式を考えることにする。
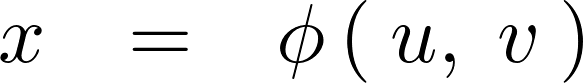
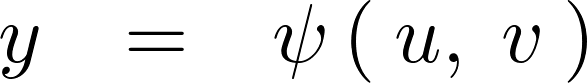
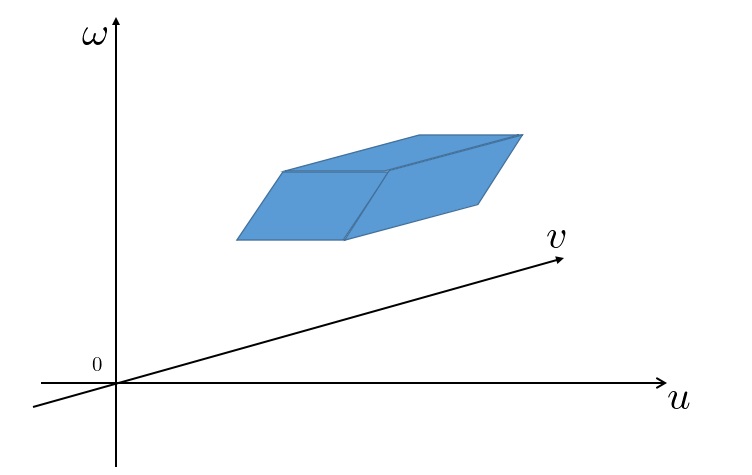
上記の関数において 平面上の点
平面上の点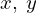 が
が 平面上の
平面上の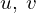 に対応するとした図形を考えた場合、一般的にこれを写像という呼び方をする。
に対応するとした図形を考えた場合、一般的にこれを写像という呼び方をする。
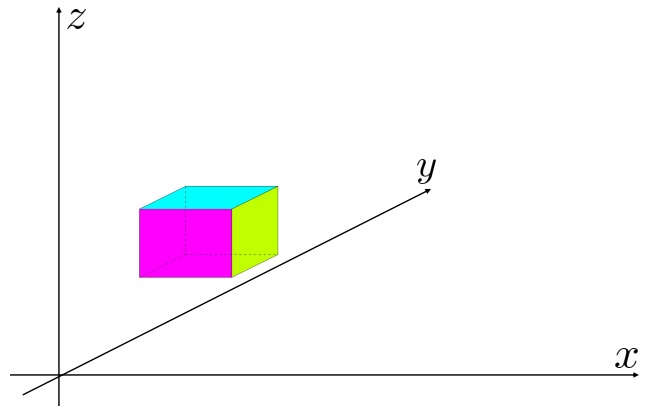
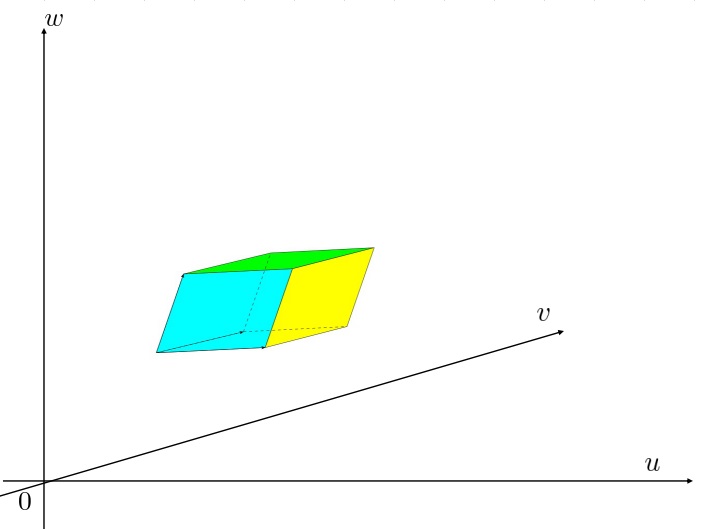
 平面上の点
平面上の点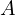 を起点にした横の長さ
を起点にした横の長さ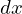 、縦の長さが
、縦の長さが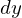 の長方形の微小面積
の長方形の微小面積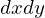 を考えてその頂点をそれぞれ
を考えてその頂点をそれぞれ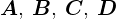 として、次のような微小面積、
として、次のような微小面積、
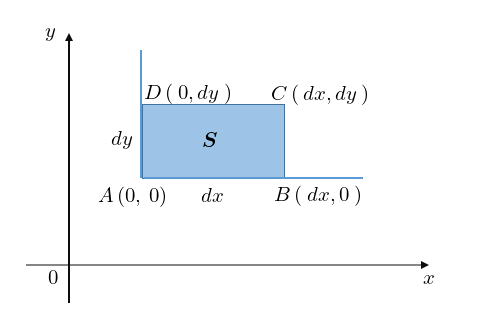
この微小面積における長方形の面積を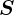 と置くことにする。
と置くことにする。
変数変換によって作られた確率密度関数を求める方法については、確率変数の変換によって求めるための公式があり、この公式を用いることで目的の確率密度関数を求めることができる。
確率変数を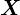 、実現値(実数)を
、実現値(実数)を で表現することにする。
で表現することにする。
仮に2つの実数として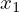 、
、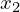 は
は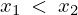 だとすると、
だとすると、
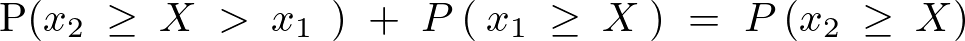
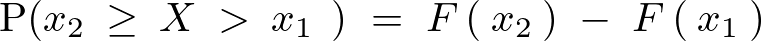
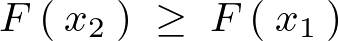
ここで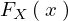 を
を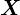 の累積分布関数(cumulative distribution function)として、この累積分布関数を次のように定義することにする。
の累積分布関数(cumulative distribution function)として、この累積分布関数を次のように定義することにする。
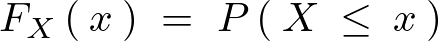
ここまで累積分布関数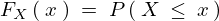 となる場合の確率なので今度は
となる場合の確率なので今度は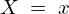 となる次のような
となる次のような の確率、
の確率、
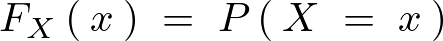
を考えて(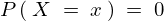 とならない)これを密度関数とする。
とならない)これを密度関数とする。
これを全域にわたって考えれば、
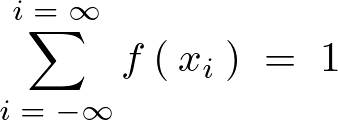
分布関数と先ほどの密度関数との関係は以下のようになる。