���ϗʊm���ϐ��̌v�Z
���ϗʊm���s��
�m���ϐ�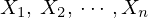 �����ɂ܂Ƃ߂�
�����ɂ܂Ƃ߂�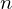 �����̏c�^�̊m���x�N�g�������̂悤�ɂ����B
�����̏c�^�̊m���x�N�g�������̂悤�ɂ����B
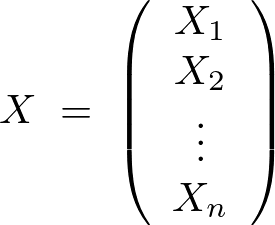
���Ɋm���ϐ������̂悤�ɔz�u�������s����m���s��Ƃ���B
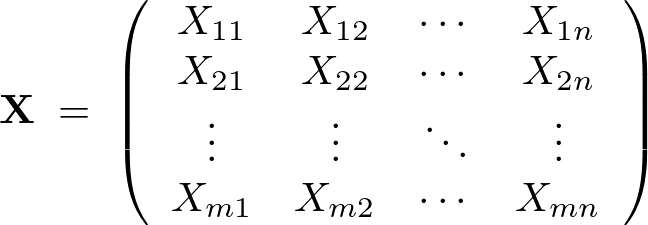
�ꉞ�����啶��X���g�p���Ă��邪��ʂ��邽�߂Ɋm���s��̂ق��̓{�[���h��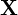 ���g���A�c�^���܂��͉��^��s�̊m���x�N�g���͑����̎Άi�{�[���h�C�^���b�N�j��
���g���A�c�^���܂��͉��^��s�̊m���x�N�g���͑����̎Άi�{�[���h�C�^���b�N�j��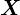 �ŕ\�����Ƃɂ���B
�ŕ\�����Ƃɂ���B
���Ғl�x�N�g��
���Ɋ��Ғl�x�N�g�����l����B
��L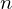 �����m���x�N�g��
�����m���x�N�g��![n�����c�^�x�N�g���ɂ�����]�u](../../img/n_dimensional_vertical_vector_transposed_small_img.png) �ɂ�������Ғl�x�N�g��
�ɂ�������Ғl�x�N�g��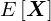 �́A
�́A

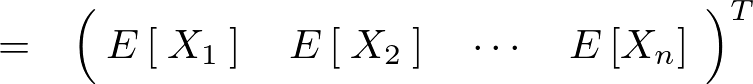
![�]�uT](../../img/t_large_img2017.png) �͓]�u�̂��ƂɂȂ�B
�͓]�u�̂��ƂɂȂ�B
���U�����U�s��
�����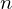 �����m���x�N�g��
�����m���x�N�g��![n�����c�^�x�N�g���ɂ�����]�u](../../img/n_dimensional_vertical_vector_transposed_small_img.png) �ɂ����āA�e
�ɂ����āA�e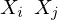 �̋����U
�̋����U![Covariance[Xi, Xj]](../../img/xiyj_cov_small_img.png) ��
��![�����U[Xi, Xj]](../../img/covariance_xi_xj_150dpi_img.png) �A���U��
�A���U��![���U[Xi, Xi]](../../img/variance_xixi_150dpi_img2.png) ��
��![���U[Xi, Xi]](../../img/variance_xixi_150dpi_img.png) �Ƃ����ꍇ�A���̎��̕��U�����U�s��
�Ƃ����ꍇ�A���̎��̕��U�����U�s��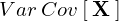 �����̂悤�ɂ������Ƃɂ���B
�����̂悤�ɂ������Ƃɂ���B
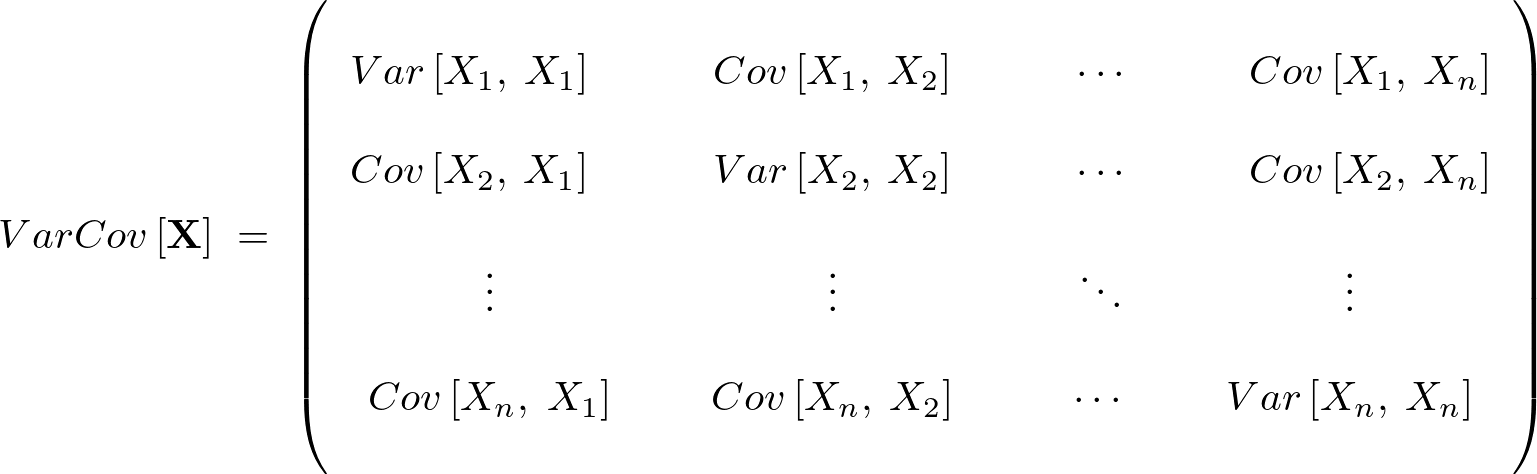
���Ғl�s��
�m���s��ɂ����ė��ӂ̊��Ғl�����A
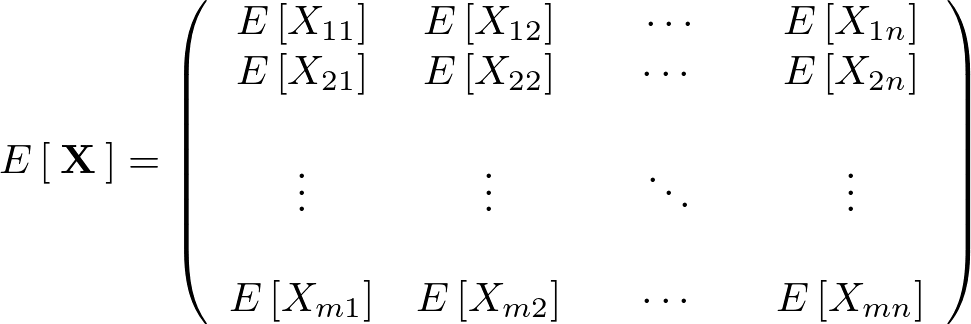
����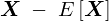 �Ƃ������e�X�̕��U���L���̊m���ϐ��x�N�g���̐ς��l����B
�Ƃ������e�X�̕��U���L���̊m���ϐ��x�N�g���̐ς��l����B
�X�̗v�f�ɂ��čl����Ύ��̂悤�ɕ\����邱�ƂɂȂ�B
���̃x�N�g���̊e�v�f���m���ϐ��ł���Ƃ�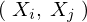 �Ƃ����ꍇ�̕Е���
�Ƃ����ꍇ�̕Е���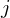 �̓Y����������ق����x�N�g���̓]�u�s��ƍl���āA
�̓Y����������ق����x�N�g���̓]�u�s��ƍl���āA
�ꎟ���ɂ����镪�U���ȉ��̂悤�ɁA
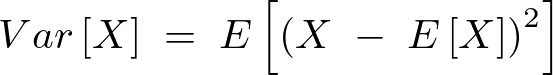
�ł��葽�������z�̏ꍇ�A�e�v�f��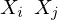 �Ɋg�������̂ł��̕��U�����U�s�����Ⴆ��
�Ɋg�������̂ł��̕��U�����U�s�����Ⴆ��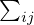 �ƒu���Ύ��̂悤�ȕ\���ƂȂ�B
�ƒu���Ύ��̂悤�ȕ\���ƂȂ�B
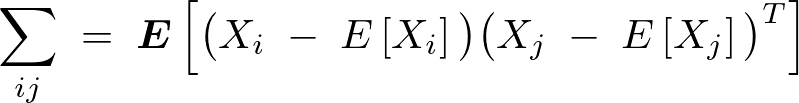
�����ő������̃x�N�g���v�f�Ԃɂ�����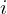 ��
��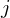 �ɂ����邻�ꂼ��ɑΉ������ςƍl���A
�ɂ����邻�ꂼ��ɑΉ������ςƍl���A![���ҒlE[Xi]](../../img/exi_probability_ex_150dpi_img.png) �̓x�N�g��
�̓x�N�g��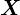 ��
��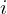 �Ԗڂ̊��Ғl�A�x�N�g��
�Ԗڂ̊��Ғl�A�x�N�g��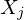 �ɂ��Ă�
�ɂ��Ă�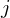 �Ԗڂ̗v�f�̊��Ғl�ł���Ƃ���A���ꂼ��ɂ����đΊp�����ɕ��U�A����ȊO�̗Ⴆ�Έ��
�Ԗڂ̗v�f�̊��Ғl�ł���Ƃ���A���ꂼ��ɂ����đΊp�����ɕ��U�A����ȊO�̗Ⴆ�Έ��![�m���x�N�g��Xi - E[Xi]](../../img/xiexi_brackets_150dpi_img.png) �ɑ��Ă��ꂼ��
�ɑ��Ă��ꂼ��![�m���x�N�g��Xj - -E[Xj]](../../img/xjexj_probability_vector_150dpi_img.png) �̓Y�������P����Y����
�̓Y�������P����Y����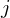 �܂œW�J�����ƍl����B
�܂œW�J�����ƍl����B
���Ȃ킿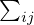 �Ƃ����s��͈ȉ��̂悤�ȍs��ł���ƍl�����邱�ƂɂȂ�B
�Ƃ����s��͈ȉ��̂悤�ȍs��ł���ƍl�����邱�ƂɂȂ�B
�����U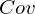 �̊e����
�̊e����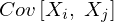 ��
��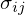 �A���U����
�A���U����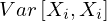 ��
��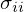 �Ƃ���Ε��U�����U�s��͌��ʂƂ��Ĉȉ��̂悤�ɂȂ�B
�Ƃ���Ε��U�����U�s��͌��ʂƂ��Ĉȉ��̂悤�ɂȂ�B
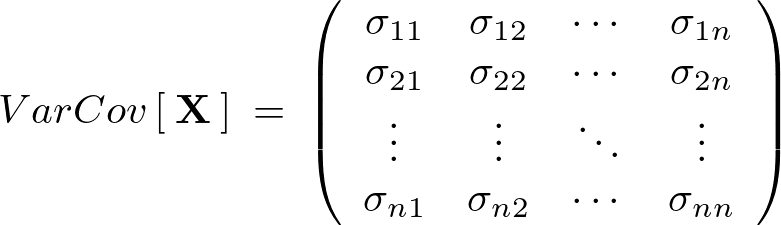
�Y�����ȂǕ\�L���ȗ����܂Ƃ߂�A
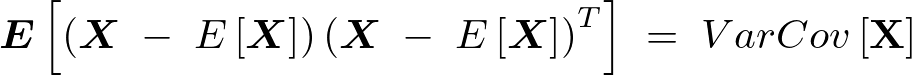
���܂܂ł�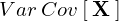 �Ƃ����\�����͎��ۂɂ͂Ȃ����̃T�C�g��ł̂ݕ\�����Ă�����̂Ȃ̂ŁA��������͌`���ɕ���ĕ��U�����U�s��̕\�L���ȉ��ɓ��ꂷ��B
�Ƃ����\�����͎��ۂɂ͂Ȃ����̃T�C�g��ł̂ݕ\�����Ă�����̂Ȃ̂ŁA��������͌`���ɕ���ĕ��U�����U�s��̕\�L���ȉ��ɓ��ꂷ��B
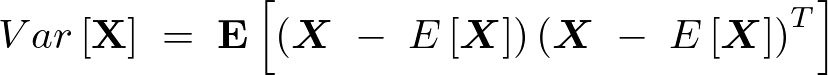
�m���x�N�g���̌v�Z
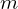 �����萔�x�N�g����
�����萔�x�N�g����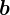 �A
�A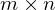 �̒萔�s���
�̒萔�s���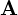 �Ƃ��Ď��̂悤�ɍl����B
�Ƃ��Ď��̂悤�ɍl����B
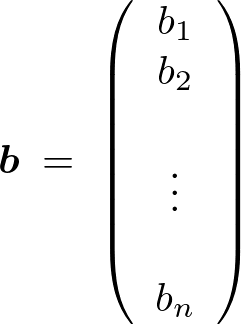
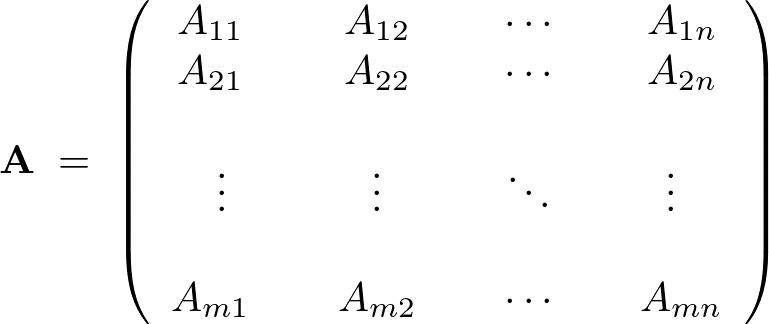
�����ɑ���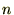 �����m���x�N�g��
�����m���x�N�g��![1�����m���x�N�g��X�]�u�\��](../../img/xx_single_dimension_transposed_matrix_150dpi_img.png) ����p���������̂悤�Ȋ��Ғl�x�N�g���̌v�Z���l�@����B
����p���������̂悤�Ȋ��Ғl�x�N�g���̌v�Z���l�@����B
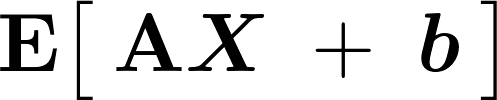
�܂���L����[]�̒���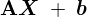 �̊e�v�f�Ɋւ��Ă��ꂼ��W�J�v�Z����B
�̊e�v�f�Ɋւ��Ă��ꂼ��W�J�v�Z����B
���������L���̊��Ғl���Ƃ�B
���̂悤�ɋ��܂�B
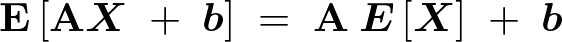
���ϗʊm���x�N�g���̕��U�����U�v�Z
����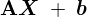 �ɂ����镪�U
�ɂ����镪�U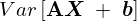 ���l�@���Ă����B
���l�@�������B
���U�Ɋւ��Ă͈ȉ��̂悤�ɕ\���ł���B
��L���Ɋւ��Ă͐�قNj��߂����ʂ��g���Ǝ��̂悤�ɕό`�ł���B
���̂悤�ɂȂ�B
��������͏�L���E�ӂ�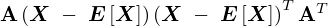 ���v�Z���Ă����B
���v�Z�������B
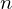 �s1��ƂP�s
�s1��ƂP�s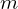 ��̍s��v�Z��
��̍s��v�Z��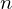 �s
�s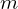 ��ɂȂ�B
��ɂȂ�B
������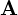 ��
��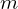 �s
�s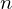 ��̒萔�s��B
��̒萔�s��B
�����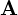 �Ƃ��̉E���̍s��̌v�Z��
�Ƃ��̉E���̍s��̌v�Z��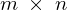 ��
��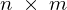 �̌v�Z�ɂȂ�B
�̌v�Z�ɂȂ�B
�����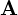 �̉������̗�
�̉������̗�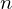 ��ƉE���̃x�N�g���̏c�̍s������������
��ƉE���̃x�N�g���̏c�̍s������������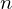 �s�Ȃ̂ł��ꂼ��ɑΉ������s��v�Z���ł��邱�ƂɂȂ�B
�s�Ȃ̂ł��ꂼ��ɑΉ������s��v�Z���ł��邱�ƂɂȂ�B
�x�N�g��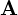 �����Ƃɖ߂�
�����Ƃɖ߂�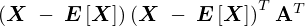 �̌v�Z�ɂ���ē���ꂽ�e�v�f���ȗ��̂���
�̌v�Z�ɂ���ē���ꂽ�e�v�f���ȗ��̂���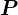 �ƒu�����Ƃɂ��Ĉȉ��̂悤�Ɍv�Z���Ă����B
�ƒu�����Ƃɂ��Ĉȉ��̂悤�Ɍv�Z���Ă����B
����ɂ��������L���̗��ӂ̊��Ғl�����B
����ď�L�̌v�Z�ɂ��萔�x�N�g���s��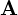 �͈ȉ��̂悤�Ɋ��Ғl
�͈ȉ��̂悤�Ɋ��Ғl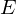 �̍����ֈړ��ł���̂Ŏ��̂悤�ɋ��܂�B
�̍����ֈړ��ł���̂Ŏ��̂悤�ɋ��܂�B
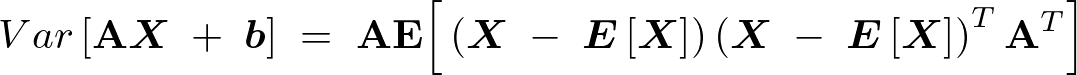
���x�͉E�ӂ�P�ƒu�������̂����Ƃɖ߂���A�̓]�u�s��Ƃ̌v�Z���l���Ă����B
�萔�x�N�g��A�����̉E���։����o���B
�ŏI�I�Ɉ�ԉE���̒萔�x�N�g���s��![�萔�s��x�N�g��A�̓]�u�s��](../../img/aa_large_transposed_vector_150dpi_img.png) ��
��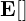 �̊O�ɏo���Ď��̂悤�ɂȂ�B
�̊O�ɏo���Ď��̂悤�ɂȂ�B
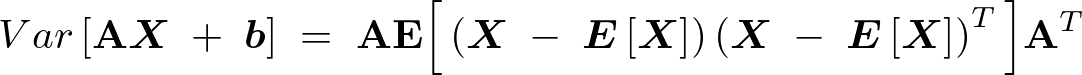
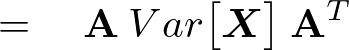
�ȏ�ɂ��đ��ϗʊm���x�N�g���ɂ��Čv�Z�������ʂ܂Ƃ߂�ƈȉ��̂悤�Ȑ��������܂�B
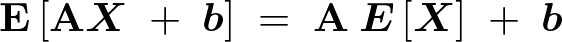
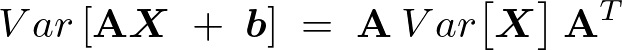
���ϗʊm���x�N�g���̌v�Z�֘A�y�[�W
- ���U�����U�s��
- ���U�����U�s��[�m���x�N�g�������ϗʐ��K���z�ɏ]���m���x�N�g���ł���ꍇ�̎��ό`�Ƃ��̓��o�̎d���̍l�@�B























