�ŗL�l�ƌŗL�x�N�g��
�l�����͈ȉ��̂悤�ɂȂ�܂��B
�܂�����x�N�g��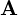 �������Ă���͂��s����̍s��́i��ʓI�ɂ́j���`���Z�q�i�ꎟ�ϊ��j�Ƃ��A
�������Ă���͂��s����̍s��́i��ʓI�ɂ́j���`���Z�q�i�ꎟ�ϊ��j�Ƃ��A
�܂�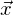 �������̗�x�N�g���Ƃ��܂��B����Ƃ��̂Ƃ��A
�������̗�x�N�g���Ƃ��܂��B����Ƃ��̂Ƃ��A
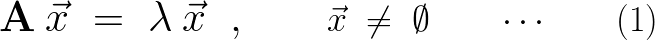
�����藧�Ȃ�A

�Ƃ����܂��B
���Ȃ݂ɗʎq�͊w�ɂ����Ă�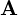 �������ʁA
�������ʁA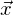 ����ԂɁA
����ԂɁA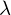 ���ϑ������l�ɑΉ����܂��B
���ϑ������l�ɑΉ����܂��B
��L��(1)��ό`����ƁA
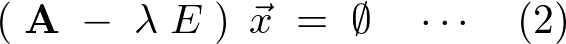
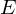 �͒P�ʍs��ł��B
�͒P�ʍs��ł��B
���܉���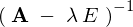 �����݂����Ƃ���ƁA�����$(2)$�̍����痼�ӂɂ�����ƁA
�����݂����Ƃ���ƁA�����$(2)$�̍����痼�ӂɂ�����ƁA
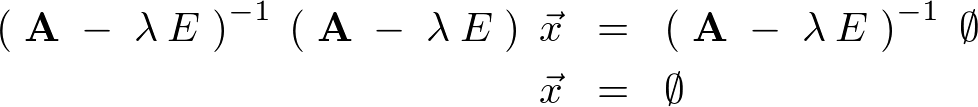
����́A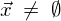 �Ƃ��������ɔ�����̂�
�Ƃ��������ɔ�����̂�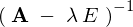 �͑��݂��Ȃ����ƂɂȂ�܂��B
�͑��݂��Ȃ����ƂɂȂ�܂��B
�]���āA
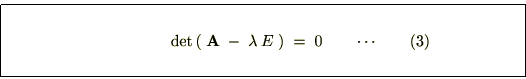
�łȂ���Ȃ�܂���B
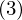 ��
��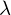 ��
��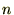 ���������i������ŗL�������Ƃ����܂��j�ƂȂ�̂ł���������ΌŗL�l
���������i������ŗL�������Ƃ����܂��j�ƂȂ�̂ł���������ΌŗL�l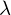 �����܂�Ƃ������@�ɂȂ�܂��i��ʓI�ɂ͂����܂�܂��j�B
�����܂�Ƃ������@�ɂȂ�܂��i��ʓI�ɂ͂����܂�܂��j�B
�ŗL�l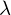 �����܂�����A���������ꂼ��
�����܂�����A���������ꂼ��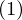 �ɑ�����A�A���������̌`�ɂ��āA�����Ă���������ΌŗL�x�N�g�������܂�܂��B
�ɑ�����A�A���������̌`�ɂ��āA�����Ă���������ΌŗL�x�N�g�������܂�܂��B
�ŗL�l�ƌŗL�x�N�g�������߂���
�ŗL�l�ƌŗL�x�N�g���̗��
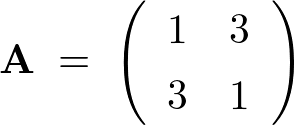

�܂��A
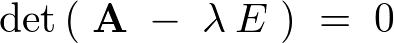
�Ȃ̂ŁA���̂悤�ɂ��ꂼ��������Ă����܂��B
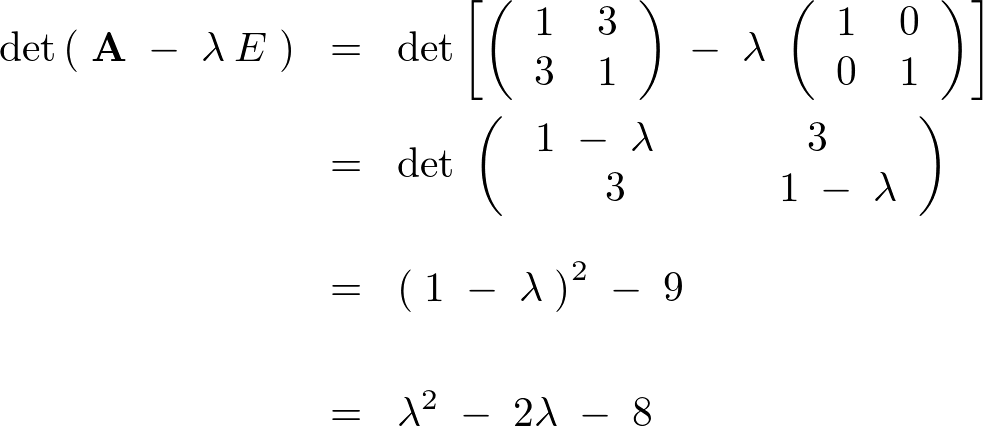
���̌��ʂɂ��ɂ͈ȉ��̂悤�ɋ��܂�܂��B
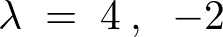
����ɂ�����
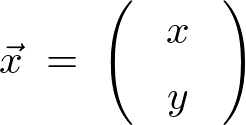
�Ƃ��܂��B
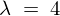 �̏ꍇ
�̏ꍇ
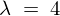 ��
��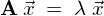 �ɑ�����āA
�ɑ�����āA
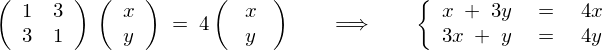
�������
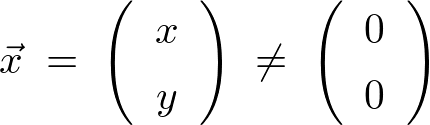
��������ƁA
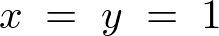
���������āA
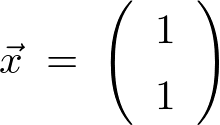
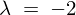 �̏ꍇ
�̏ꍇ
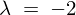 ��
��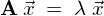 �ɑ�����܂��B
�ɑ�����܂��B
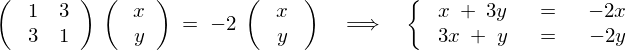
��������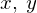 ��������ƁA
��������ƁA

�ɂȂ�܂��B
�Ȃ̂ŁA
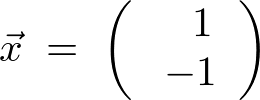
�ȏ�̌��ʂ���A
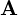 �̌ŗL�l
�̌ŗL�l
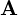 �̌ŗL�l�́A
�̌ŗL�l�́A
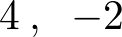
�ŗL�l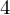 �ɑ�����ŗL�x�N�g��
�ɑ�����ŗL�x�N�g��
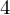 �ɑ�����ŗL�x�N�g���́A
�ɑ�����ŗL�x�N�g���́A
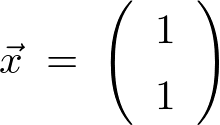
�ŗL�l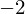 �ɑ�����ŗL�x�N�g��
�ɑ�����ŗL�x�N�g��
�ŗL�l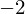 �ɑ�����ŗL�x�N�g���́A
�ɑ�����ŗL�x�N�g���́A
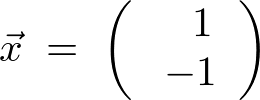
�ŗL�l�ƌŗL�x�N�g���֘A�y�[�W
- �s��
- ���T�C�g�͎�ɕ����Ɋւ��鐔�w�ȂǁA���̑����ӂ��܂߂����X�������ς̃E�F�u�T�C�g�ł��B ���w����Ɋւ��Ă̎�|�Ƃ��ẮA�ʏ�̃e�L�X�g�ł͊�������Ă��܂����e�Ȃǂ��ڂ����L�q���A����ɂ͓������������̂ł͂Ȃ��A�킩��ɂ������e�������ɂ킩��₷���`���邩���ȂǁA�����������E�F�u�R���e���c�Ȃ�ł̗͂����Ƌ@�����������T�C�g�쐬�����Ƃ��Ă��܂��B
- �s�̌v�Z�|����
- ���T�C�g�͎�ɕ����Ɋւ��鐔�w�ȂǁA���̑����ӂ��܂߂����X�������ς̃E�F�u�T�C�g�ł��B ���w����Ɋւ��Ă̎�|�Ƃ��ẮA�ʏ�̃e�L�X�g�ł͊�������Ă��܂����e�Ȃǂ��ڂ����L�q���A����ɂ͓������������̂ł͂Ȃ��A�킩��ɂ������e�������ɂ킩��₷���`���邩���ȂǁA�����������E�F�u�R���e���c�Ȃ�ł̗͂����Ƌ@�����������T�C�g�쐬�����Ƃ��Ă��܂��B
- �t�s��
- ���T�C�g�͎�ɕ����Ɋւ��鐔�w�ȂǁA���̑����ӂ��܂߂����X�������ς̃E�F�u�T�C�g�ł��B ���w����Ɋւ��Ă̎�|�Ƃ��ẮA�ʏ�̃e�L�X�g�ł͊�������Ă��܂����e�Ȃǂ��ڂ����L�q���A����ɂ͓������������̂ł͂Ȃ��A�킩��ɂ������e�������ɂ킩��₷���`���邩���ȂǁA�����������E�F�u�R���e���c�Ȃ�ł̗͂����Ƌ@�����������T�C�g�쐬�����Ƃ��Ă��܂��B
- �t�s��̌v�Z�|����
- ���T�C�g�͎�ɕ����Ɋւ��鐔�w�ȂǁA���̑����ӂ��܂߂����X�������ς̃E�F�u�T�C�g�ł��B ���w����Ɋւ��Ă̎�|�Ƃ��ẮA�ʏ�̃e�L�X�g�ł͊�������Ă��܂����e�Ȃǂ��ڂ����L�q���A����ɂ͓������������̂ł͂Ȃ��A�킩��ɂ������e�������ɂ킩��₷���`���邩���ȂǁA�����������E�F�u�R���e���c�Ȃ�ł̗͂����Ƌ@�����������T�C�g�쐬�����Ƃ��Ă��܂��B
- �s���g�����A���������̉�@
- ���T�C�g�͎�ɕ����Ɋւ��鐔�w�ȂǁA���̑����ӂ��܂߂����X�������ς̃E�F�u�T�C�g�ł��B ���w����Ɋւ��Ă̎�|�Ƃ��ẮA�ʏ�̃e�L�X�g�ł͊�������Ă��܂����e�Ȃǂ��ڂ����L�q���A����ɂ͓������������̂ł͂Ȃ��A�킩��ɂ������e�������ɂ킩��₷���`���邩���ȂǁA�����������E�F�u�R���e���c�Ȃ�ł̗͂����Ƌ@�����������T�C�g�쐬�����Ƃ��Ă��܂��B
- �s���g�����A���������̉�����
- ���T�C�g�͎�ɕ����Ɋւ��鐔�w�ȂǁA���̑����ӂ��܂߂����X�������ς̃E�F�u�T�C�g�ł��B ���w����Ɋւ��Ă̎�|�Ƃ��ẮA�ʏ�̃e�L�X�g�ł͊�������Ă��܂����e�Ȃǂ��ڂ����L�q���A����ɂ͓������������̂ł͂Ȃ��A�킩��ɂ������e�������ɂ킩��₷���`���邩���ȂǁA�����������E�F�u�R���e���c�Ȃ�ł̗͂����Ƌ@�����������T�C�g�쐬�����Ƃ��Ă��܂��B
- �K�i��
- ���T�C�g�͎�ɕ����Ɋւ��鐔�w�ȂǁA���̑����ӂ��܂߂����X�������ς̃E�F�u�T�C�g�ł��B ���w����Ɋւ��Ă̎�|�Ƃ��ẮA�ʏ�̃e�L�X�g�ł͊�������Ă��܂����e�Ȃǂ��ڂ����L�q���A����ɂ͓������������̂ł͂Ȃ��A�킩��ɂ������e�������ɂ킩��₷���`���邩���ȂǁA�����������E�F�u�R���e���c�Ȃ�ł̗͂����Ƌ@�����������T�C�g�쐬�����Ƃ��Ă��܂��B
- �Ίp��
- ���T�C�g�͎�ɕ����Ɋւ��鐔�w�ȂǁA���̑����ӂ��܂߂����X�������ς̃E�F�u�T�C�g�ł��B ���w����Ɋւ��Ă̎�|�Ƃ��ẮA�ʏ�̃e�L�X�g�ł͊�������Ă��܂����e�Ȃǂ��ڂ����L�q���A����ɂ͓������������̂ł͂Ȃ��A�킩��ɂ������e�������ɂ킩��₷���`���邩���ȂǁA�����������E�F�u�R���e���c�Ȃ�ł̗͂����Ƌ@�����������T�C�g�쐬�����Ƃ��Ă��܂��B


























