�t�[���G�ϕ�
���A�����I�ł͂Ȃ������������Ƃ��܂��B
���̂Ƃ��A
| ���� |  |
|---|
�ƍl���邱�Ƃ��o���邩�Ǝv���܂��B
�����������Ƃ��A�t�[���G�����̓t�[���G�ϕ��Ƃ�����̂ɂȂ�܂��B
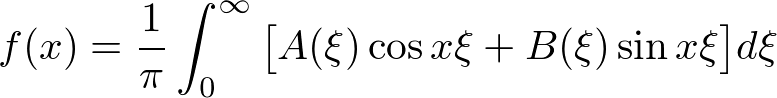
��L����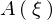 �A
�A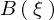 �͈ȉ��̂悤�ɂȂ�܂��B
�͈ȉ��̂悤�ɂȂ�܂��B
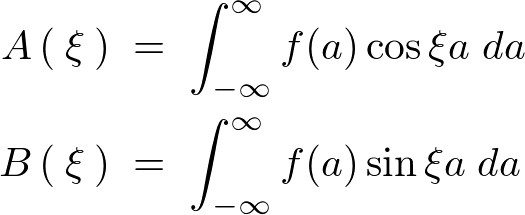
���ۂɑ�����Ă݂�ƁA
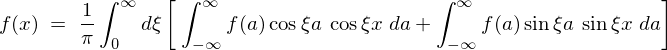
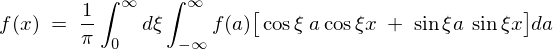
�����ŎO�p���̊W��
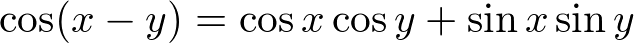
���A
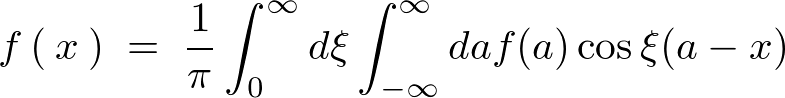
������t�[���G�ϕ������ȂǂƂ������肵�܂��B
�M�`���������������ۂɂ��̏�L�̌����ɗႦ�Ώ搔�ɕϐ�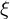 �̂���
�̂���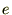 ���ꏏ�ɂ���ꍇ�̌v�Z���K�v�ɂȂ�܂��B
���ꏏ�ɂ���ꍇ�̌v�Z���K�v�ɂȂ�܂��B
�ꉞ�����������ꍇ�̐ϕ�����������悤�Ȃ̂ł����A���ꂾ�Ɖ��p�������Ȃ��̂ŗ��ł��̉�@�����������Ǝv���܂��B
���������̐ϕ��͓������o���܂ł����X���ł��B
��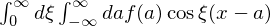 �̋��ߕ���
�̋��ߕ���
�܂��ϕ�������ύX���܂��B
���̏ꍇ�A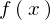 ���L�E����ΐϕ��ł���Ȃ�ΐϕ������̕ϊ����\�ł��B
���L�E����ΐϕ��ł���Ȃ�ΐϕ������̕ϊ����\�ł��B
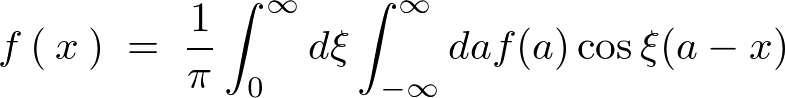
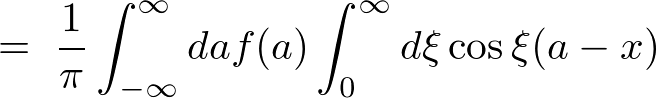
���̂Ƃ��̐ϕ����A
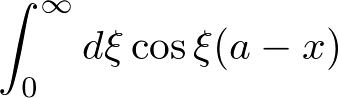
�ɂ��čl���Č��܂��傤�B
�Ⴆ�A���̂悤�ȏꍇ�̐ϕ����������@���ڂ������܂��B
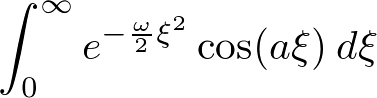
�܂����߂�ϕ���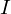 �Ƃ����܂��B
�Ƃ����܂��B
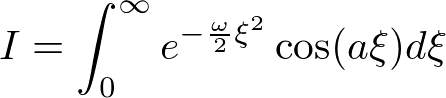
������܂�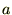 �ŕΔ������Ă݂܂傤�B
�ŕΔ������Ă݂܂傤�B
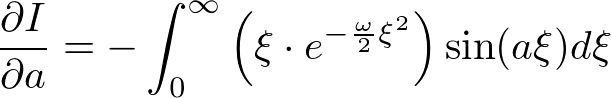
�����ŁA
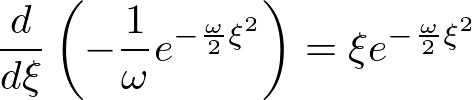
�Ƃ����W�𗘗p���A�����ϕ�������ƁA
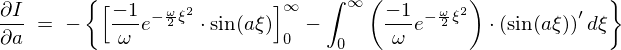
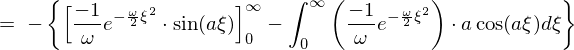
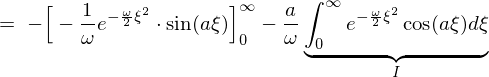
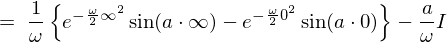
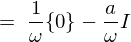
���̌��ʂɂ��ȉ��̂悤�Ȕ�����������������܂��B
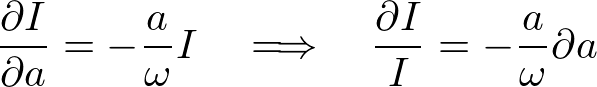
���̔����������̉������߂܂��B
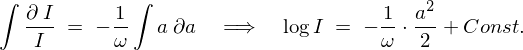
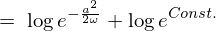
�ΐ��̐����ɂ��w���̒萔��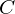 �ƒu���Έȉ��̂悤�Ȏ������܂�܂��B
�ƒu���Έȉ��̂悤�Ȏ������܂�܂��B
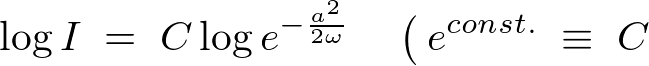
����ɗ��ӂ̑ΐ����Ƃ�Έȉ��̂悤�ɋ��܂�܂��B
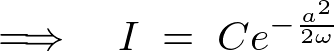
���ɂ��̐ϕ��萔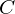 �����߂܂��B
�����߂܂��B
�d�v�Ȃ��Ƃ͂���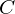 �Ƃ����ϕ��萔��
�Ƃ����ϕ��萔��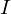 �̕ϐ���
�̕ϐ���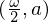 �Ƃ���
�Ƃ���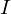 ��
��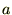 �ɂ��Đϕ��������̂Ȃ̂����瓖�R�o�Ă����ϕ��萔
�ɂ��Đϕ��������̂Ȃ̂����瓖�R�o�Ă����ϕ��萔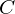 ��
��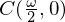 �ł���Ƃ������ƂɂȂ�܂��B
�ł���Ƃ������ƂɂȂ�܂��B
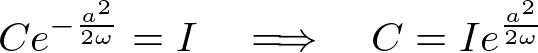
���A
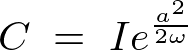
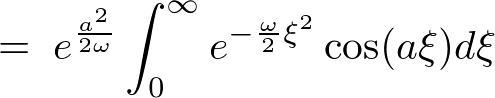
������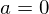 �Ȃ̂ŁA
�Ȃ̂ŁA
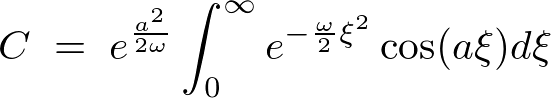
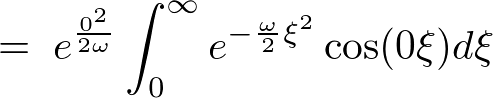
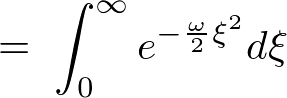
��L��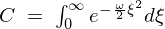 �����߂邽�߂ɂ܂��ϕ��͈͂��L���ċ��߂�ϕ��l��2�{�ɂ��܂��i
�����߂邽�߂ɂ܂��ϕ��͈͂��L���ċ��߂�ϕ��l��2�{�ɂ��܂��i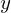 ��Ώ̂ɍL�����Ă��邽�߂ɉ\�ł��j�B
��Ώ̂ɍL�����Ă��邽�߂ɉ\�ł��j�B
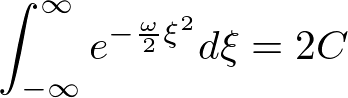
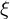 �ɂ��Ă̕ϐ��ϊ������s���邽�߂�
�ɂ��Ă̕ϐ��ϊ������s���邽�߂�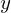 �Ɋւ��Ă̎������̂悤�ɒu���܂��B
�Ɋւ��Ă̎������̂悤�ɒu���܂��B
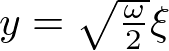
���̎��Ɋւ��� �ŕϐ��ϊ����Ă����܂��B
�ŕϐ��ϊ����Ă����܂��B
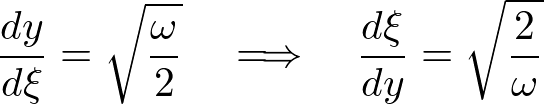
����ɂ��A
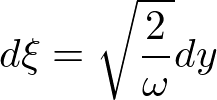
�����������A
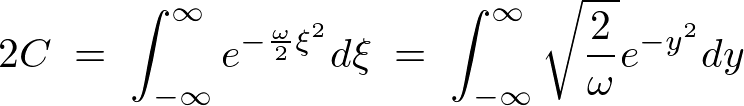
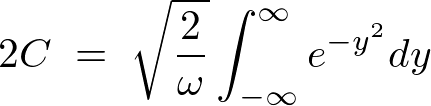
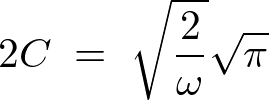
���̂悤�ɋ��܂�܂��B
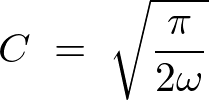
�܂��r���̎��̐ϕ������K�E�X�ϕ�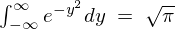 ���g���Ă��܂��B
���g���Ă��܂��B
�����Ă����ɂ���Ď��̂悤�ɋ��߂��܂��B
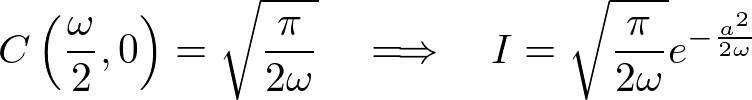
����ċ��߂�ϕ��̒l�͎��̂悤�ɋ��܂�܂��B
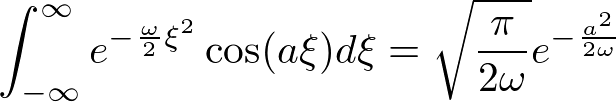
�t�[���G�ϕ��֘A�y�[�W
- �t�[���G�����W�J
- �u���b�N�V���[���Y���f���Ƃ́A���Z�H�w�ɂ�����I�v�V�����̉��i����̍ۂɕK�v�Ȍv�Z���f���̂��Ƃ��w���܂��B���̃`���v�^�[�ł̓u���b�N�V���[���Y���f���Δ����������ӂ��ߒ��ɂ����ďd�v�ɂȂ�t�[���G��͂Ɋւ��ĉ�����Ă����܂��B
- �t�[���G�����W�J�E�]���W�J
- �u���b�N�V���[���Y���f���Ƃ́A���Z�H�w�ɂ�����I�v�V�����̉��i����̍ۂɕK�v�Ȍv�Z���f���̂��Ƃ��w���܂��B���̃`���v�^�[�ł̓u���b�N�V���[���Y���f���Δ����������ӂ��ߒ��ɂ����ďd�v�ɂȂ�t�[���G��͂Ɋւ��ĉ�����Ă����܂��B


























