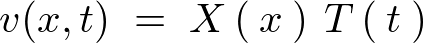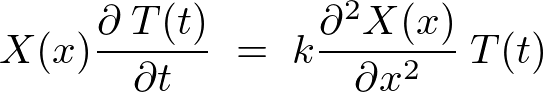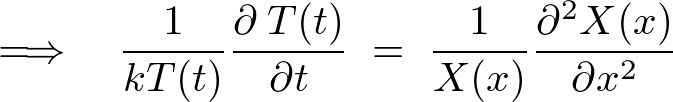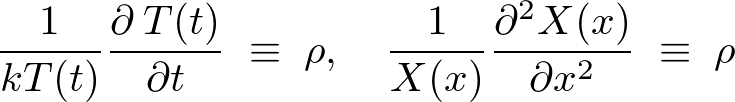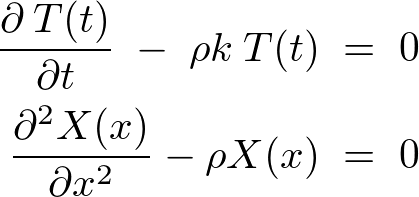������Ԃɂ�����M�`���������i�g�U�������j�ƃt�[���G�ϕ�
�O�Z�N�V�����ł͒��Ԃɂ����Ă̈ꎟ���M�`�������������܂��������x�́A
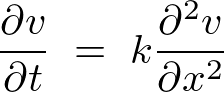
�ɂ��Ė����ɒ����ꍇ�i������ԁj�̕��������l���Ă݂邱�Ƃɂ��܂��傤�B
�ϕ��͈͂�������ԂƂȂ�̂ł��̏ꍇ�̓t�[���G�ϕ��\�����K�p�ł���悤�ɂȂ�܂��B
- ��������
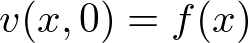
�����悤�ɕϐ��������s�����ꂼ��̒萔��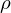 �Ƃ��܂��B
�Ƃ��܂��B
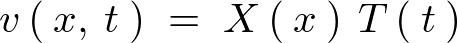
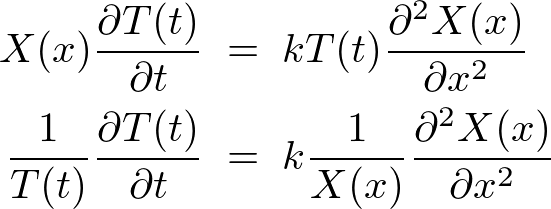
�E�ӂ� �̊��A���ӂ�
�̊��A���ӂ� �̊��ɂȂ��Ă��܂��̂ŁA���ꂼ���萔
�̊��ɂȂ��Ă��܂��̂ŁA���ꂼ���萔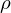 �Ƃ݂Ȃ��Ď������܂��B
�Ƃ݂Ȃ��Ď������܂��B
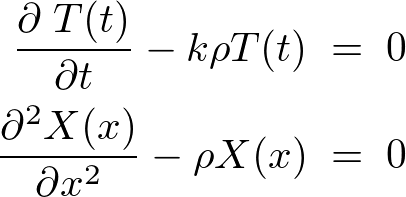
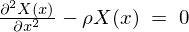 �ɂ���
�ɂ���
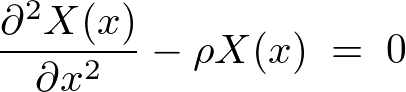
�ɂ��Ă̓����������́A
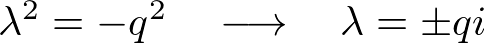
�Ȃ̂Ŋ�{���́A
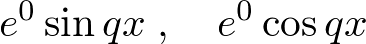
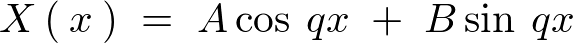



 �����̕������̉��Ȃ���̐��`���������ƂȂ�܂��B
�����̕������̉��Ȃ���̐��`���������ƂȂ�܂��B �ł͂Ȃ�
�ł͂Ȃ� �ɂȂ��Ă���܂����B���������l�ѐ\���グ�܂��B
�ɂȂ��Ă���܂����B���������l�ѐ\���グ�܂��B