������Ԃɂ�����M�`���������i�g�U�������j�Ɋւ�����Ƃ��̉�@
������Ԃɂ�����M�`���������i�g�U�������j�ƃt�[���G�ϕ�
�O�Z�N�V�����ł͒��Ԃɂ����Ă̈ꎟ���M�`�������������܂��������x�́A
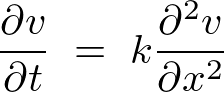
�ɂ��Ė����ɒ����ꍇ�i������ԁj�̕��������l���Ă݂邱�Ƃɂ��܂��傤�B
�ϕ��͈͂�������ԂƂȂ�̂ł��̏ꍇ�̓t�[���G�ϕ��\�����K�p�ł���悤�ɂȂ�܂��B
- ��������
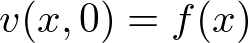
�����悤�ɕϐ��������s�����ꂼ��̒萔��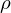 �Ƃ��܂��B
�Ƃ��܂��B
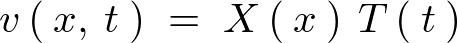
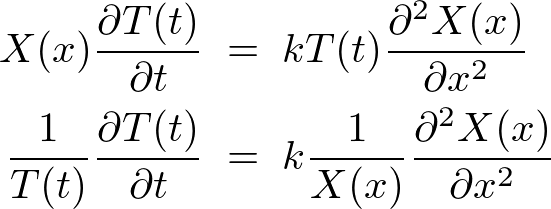
�E�ӂ� �̊��A���ӂ�
�̊��A���ӂ� �̊��ɂȂ��Ă��܂��̂ŁA���ꂼ���萔
�̊��ɂȂ��Ă��܂��̂ŁA���ꂼ���萔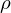 �Ƃ݂Ȃ��Ď������܂��B
�Ƃ݂Ȃ��Ď������܂��B
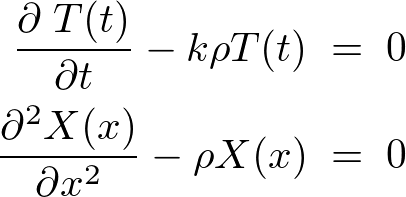
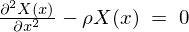 �ɂ���
�ɂ���
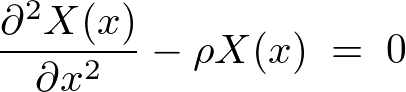
�ɂ��Ă̓����������́A
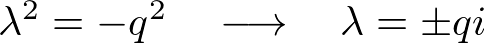
�Ȃ̂Ŋ�{���́A
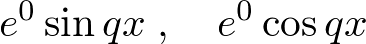
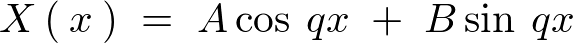
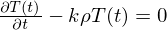 �ɂ���
�ɂ���
����,
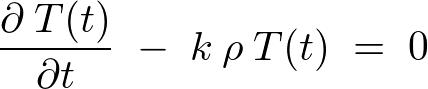
�Ɋւ��āA
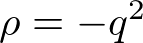
��������ƁA
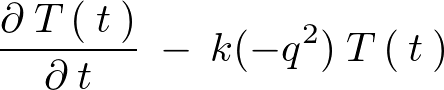
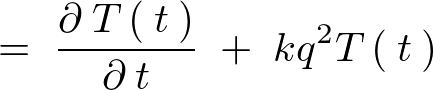
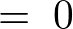
�ƂȂ�̂ňȉ��̂悤�Ȕ������������łĂ��܂��B
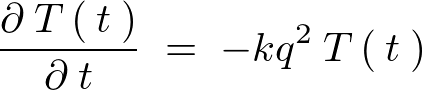
�Ƃ������������������łĂ��܂��B
����������Ă����܂��B
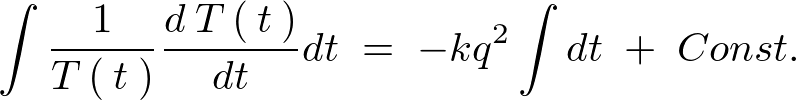
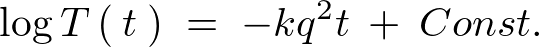
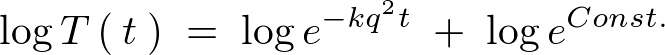
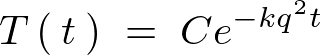
�����̌��ʂ��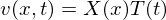 �́A
�́A
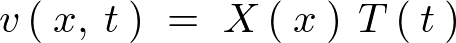
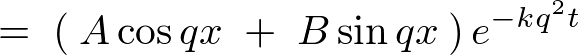
��L�̒萔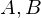 �ɂ͂��ꂼ��̒���
�ɂ͂��ꂼ��̒���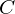 ���g�ݍ���ł�����̂Ƃ��Ă��܂��i�P�ɕ\�L���ȗ������Ă��܂��j�B
���g�ݍ���ł�����̂Ƃ��Ă��܂��i�P�ɕ\�L���ȗ������Ă��܂��j�B
�㎮�̉��ɂ����Đ��`�����Ȃ̂ł���ɂ��d�ˍ��킹���܂����ɂȂ�Ƃ������Ƃ��l����A
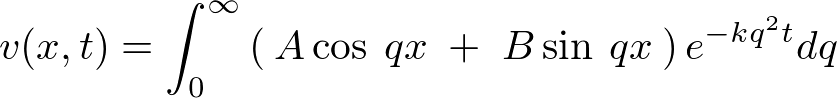
�ƕ\���ł��܂��B
����ɂ�����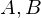 ��
��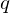 �̊��ƍl�����ꍇ�A
�̊��ƍl�����ꍇ�A
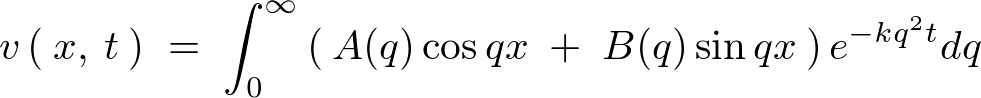
���̎����ȉ��Ɏ������������A
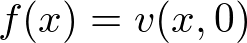
�����悤�ɂ��܂��B
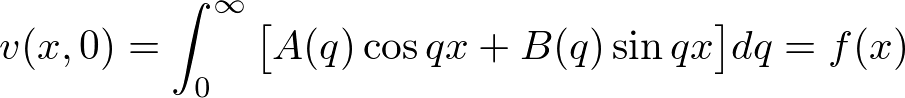
������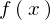 �̃t�[���G�ϕ��\����K�p����A
�̃t�[���G�ϕ��\����K�p����A
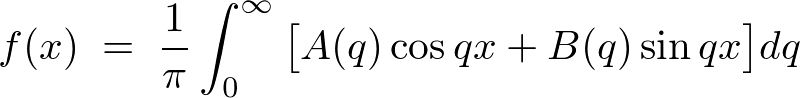
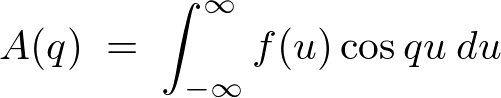
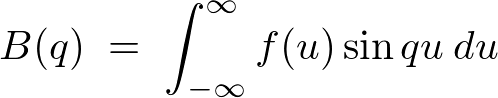
�ƂȂ�̂ő�����āA
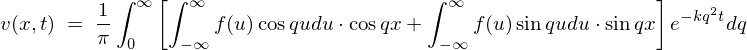
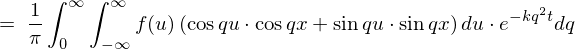
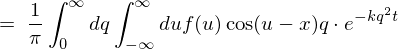
�����Ŏ������Ƃ����̂ɂ��ďq�ׂ�ƁA�t�[���G�ϕ��Ƃ����̂́A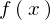 ��
��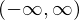 �Ƃ����͈͂ɂ����Đ�ΐϕ��\�ł���A����ɂ͂���
�Ƃ����͈͂ɂ����Đ�ΐϕ��\�ł���A����ɂ͂���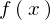 ���L�E�i�������ɒ����_�Ƃ��Ă��܂����A
���L�E�i�������ɒ����_�Ƃ��Ă��܂����A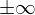 �ŗL�E�i
�ŗL�E�i �Ƃ����O��̂��߁j�ł���Ƃ������̂Q�̏��������ΐϕ������̌������\�ɂȂ�܂��B
�Ƃ����O��̂��߁j�ł���Ƃ������̂Q�̏��������ΐϕ������̌������\�ɂȂ�܂��B
��������Ǝ��̂悤�ɂł��܂��B
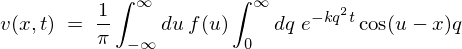
��قǂ̃Z�N�V�����i�ꎟ���M�`���������j��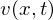 �ƈႤ�Ƃ���́A������ԁi�ɂ�����M�`���������j�Ƃ����O��̂��߂Ƀt�[���G�ϕ��ɂȂ�̂ł����āA���̃t�[���G�ϕ��Ƃ��������̂��߂ɐV�����A
�ƈႤ�Ƃ���́A������ԁi�ɂ�����M�`���������j�Ƃ����O��̂��߂Ƀt�[���G�ϕ��ɂȂ�̂ł����āA���̃t�[���G�ϕ��Ƃ��������̂��߂ɐV�����A
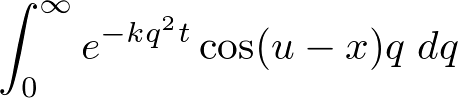
�̕����̌v�Z���K�v�ɂȂ��Ă��邱�Ƃł��B
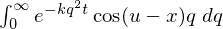 �̌v�Z
�̌v�Z
�܂����߂�ϕ���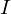 �ƒu���܂��B
�ƒu���܂��B
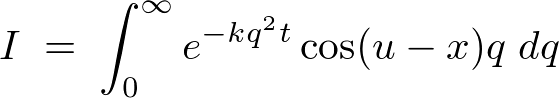
�����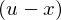 �ŕΔ������܂��B
�ŕΔ������܂��B
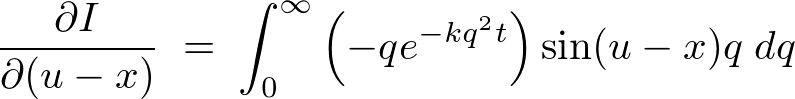
�㎮�̉E�ӂɑ��ĕ����ϕ������s���܂��B
�����ϕ��̌����A
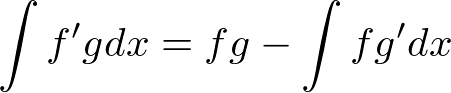
�ɓ��Ă͂߂���ꂼ��A
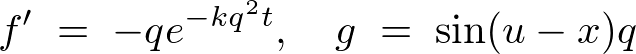
�ƂȂ�̂ŘA�����i�`�F�C���j���g���A���̂悤�ɔ������Ă����܂��B
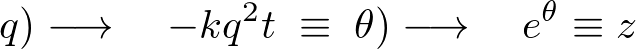
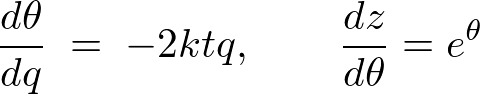
���A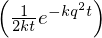 ��
��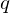 �ɂ��Ĕ����������ʂ́A
�ɂ��Ĕ����������ʂ́A
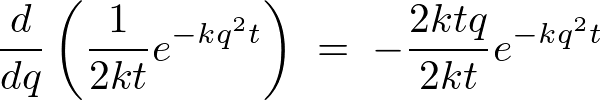
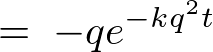
�ƂȂ�̂ł���𗘗p����A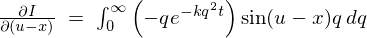 ���̉E�ӂ̕����ϕ��́A
���̉E�ӂ̕����ϕ��́A
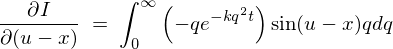
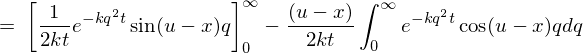
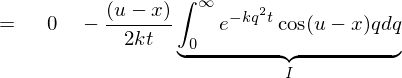
�Ƃ������ʂ��A
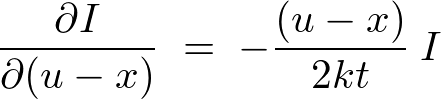
�ƂȂ�܂��B
���̔����������������Ă����܂��傤�B
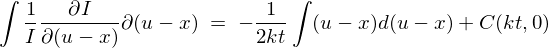
�����̃R���e���c
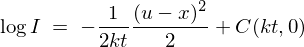
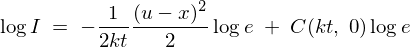
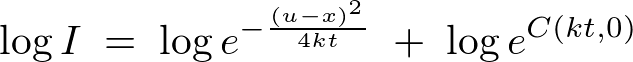
������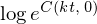 ��
��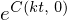 �����₷���悤�ɂ�����
�����₷���悤�ɂ�����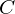 �ƕ\�L���܂��B
�ƕ\�L���܂��B
����ƁA
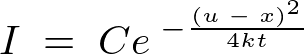
�Ƃ����������ɂȂ�܂��B
���ɂ��̒萔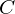 �ɂ��čl�@���Ă݂�ƁA����
�ɂ��čl�@���Ă݂�ƁA����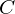 ��
��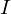 �̕ϐ���
�̕ϐ���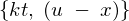 �Ƃ���
�Ƃ���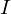 ��
��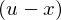 �ɂ��Đϕ��������̂Ȃ̂ŁA���R�łĂ����ϕ��萔
�ɂ��Đϕ��������̂Ȃ̂ŁA���R�łĂ����ϕ��萔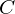 ��
��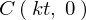 ���Ƃ������Ƃɂ���܂��B
���Ƃ������Ƃɂ���܂��B
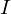 �����ɖ߂��A
�����ɖ߂��A
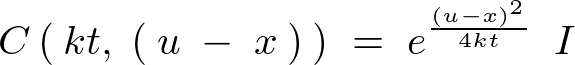
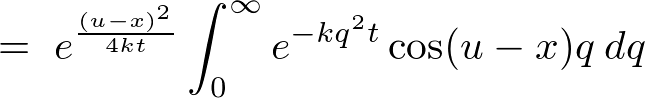
������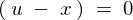 �Ȃ̂ŁA
�Ȃ̂ŁA
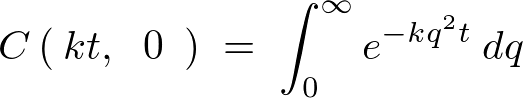
�����ŏo�Ă������̎��ɃK�E�X�ϕ��������K�p�ł���悤�ɐϕ��͈͂��L���܂��B
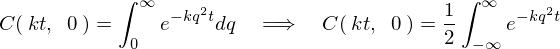
�E�ӂ̐ϕ������s���邽�߂ɕϐ��ϊ������܂��B
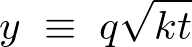
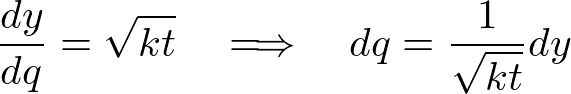
�������A
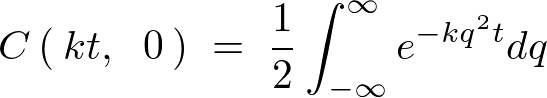
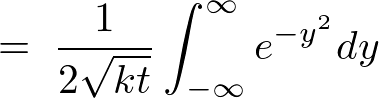
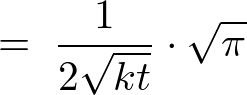
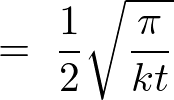
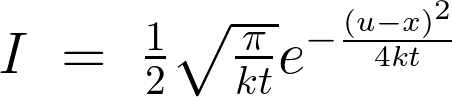
����ɂ��ȉ��̂悤�ɂȂ�܂��B
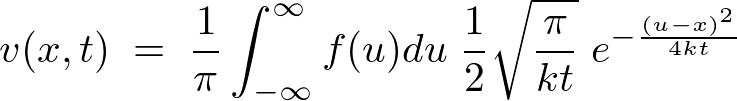
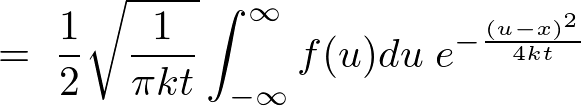
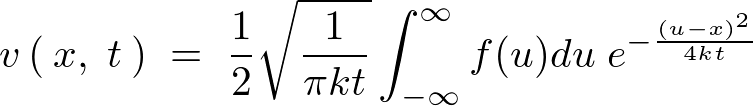
������Ԃɂ�����M�`���������֘A�y�[�W
- �M�`��������
- �u���b�N�V���[���Y���f���Ƃ́A���Z�H�w�ɂ�����I�v�V�����̉��i����̍ۂɕK�v�Ȍv�Z���f���̂��Ƃ��w���܂��B���T�C�g�͂��̃u���b�N�V���[���Y�Δ����������̓��o�ߒ������ł͂Ȃ����������߂̏������w����J�ɉ�������T�C�g�ɂȂ�܂��B���̃`���v�^�[�ł͔M�`���������ɂ����鋫�E�l���Ɋւ�����ɂ��čl�@���Ă����܂��B���̃Z�N�V�����ł͕����^�Δ����������i�M�`���������j�ɂ�鋫�E�l�Ɋւ��Ă̖��Ƃ��̉�@�ɂ��čl�@���Ă����܂��B


























