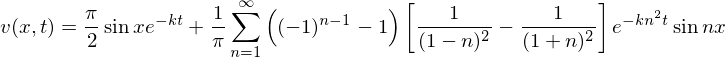�M�`���������ɂ�鋫�E�l�Ɋւ��Ă̖��Ƃ��̉�@
�M�`���������i�g�U�������j�ɂ�����d�ˍ��킹�̌���
���m�����܂܂Ȃ������ł��Ȃ��Ƃ����Ƃ������̓������`�Δ����������ɂ����Ắg�d�ˍ��킹�̌����h�Ƃ����̂����藧���܂��B
�܂�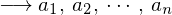 �����̕������̉��Ȃ���̐��`���������ƂȂ�܂��B
�����̕������̉��Ȃ���̐��`���������ƂȂ�܂��B
���̂悤�Ȏ����l���Ă݂܂��傤�B
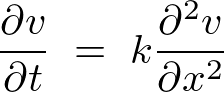
���j20211107�����B�E�ӕϐ���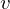 �ł͂Ȃ�
�ł͂Ȃ�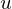 �ɂȂ��Ă���܂����B���������l�ѐ\���グ�܂��B
�ɂȂ��Ă���܂����B���������l�ѐ\���グ�܂��B
�ϐ������@���g���āA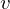 ��
�� ��
�� �̊��Ƃ��ē�ɕ������܂��B
�̊��Ƃ��ē�ɕ������܂��B
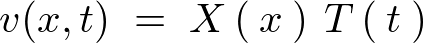
������㎮�ɑ������ƁA
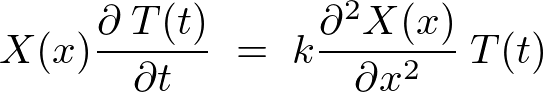
����ɂ����� �̍���
�̍��� �̍����ȉ��̂悤�ɍ��E��ɕ��ޕ��������܂�
�̍����ȉ��̂悤�ɍ��E��ɕ��ޕ��������܂�
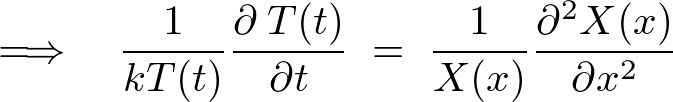
���̗��ӂ��悭���Ă݂�Ƃ��ꂼ�ꂪ ��
�� �����̊��ɂȂ��Ă��邱�Ƃ��킩��Ǝv���܂��B
�����̊��ɂȂ��Ă��邱�Ƃ��킩��Ǝv���܂��B
�㎮�̂悤�� ��
�� ��Ɨ��ɍl���Ă����������藧���߂ɂ͗��ӂ̒l���萔�ł���ƍl����悭�A���̒萔�����ꂼ��̎��ɑ��āA
��Ɨ��ɍl���Ă����������藧���߂ɂ͗��ӂ̒l���萔�ł���ƍl����悭�A���̒萔�����ꂼ��̎��ɑ��āA
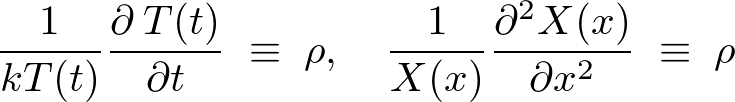
�ƒu���ƁA
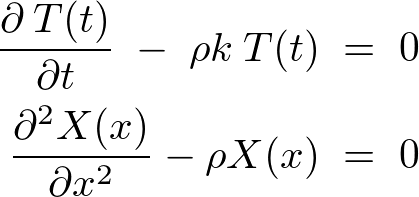
�Ƃ����Q�̕������ŕ\���܂��B
���E�����̕t�^
������ȉ��Ɏ��������|
���E����
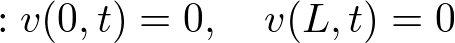
����сA���������A
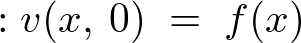
�̂��Ƃɂ��̉������߂Ă݂܂��傤�B
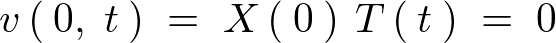
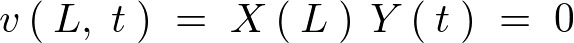
�ƍl������̂ŁA
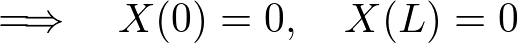
�Ƃ����Q�̏����������̂��܂����߂܂��B
�܂��A
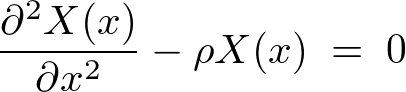
�̉��ŋ��E�����A
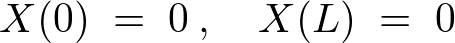
�������͎̂��̂R��ނ��l�����܂��B
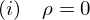 �̂Ƃ�
�̂Ƃ�
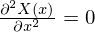 �ɂȂ�̂ň�ʉ��́A
�ɂȂ�̂ň�ʉ��́A
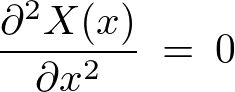
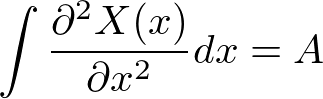
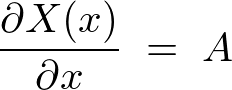
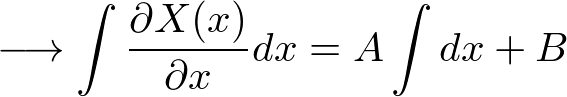
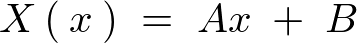
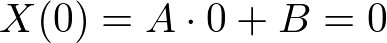
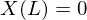 �̏����A
�̏����A
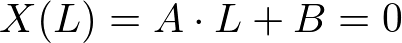

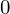 �ƂȂ���Ƃ��Ă͈Ӗ�������܂���B�B
�ƂȂ���Ƃ��Ă͈Ӗ�������܂���B�B
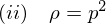 �̂Ƃ�
�̂Ƃ�
��ʉ��́A
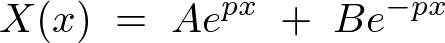
�ƂȂ�̂ŁA�������A
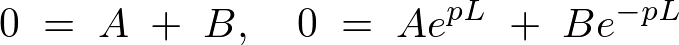
�ƂȂ�܂��B
���̏ꍇ���ĂсA
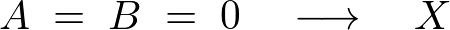
��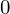 �ƂȂ�̂�
�ƂȂ�̂� �Ɠ����悤�ɉ��Ƃ��Ă͈Ӗ�������܂���B
�Ɠ����悤�ɉ��Ƃ��Ă͈Ӗ�������܂���B
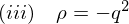 �̂Ƃ�
�̂Ƃ�
�ł͍Ō��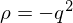 �͂ǂ��Ȃ�ł��傤���H���ۂɂ���Ă݂�ƁA
�͂ǂ��Ȃ�ł��傤���H���ۂɂ���Ă݂�ƁA
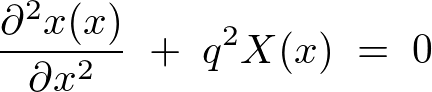
�ƂȂ�̂ʼn��͎��Ɏ����A
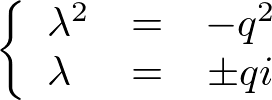
�Ƃ����悤�ȕ��f���ɂȂ�܂��B
������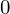 �A�@������
�A�@������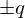 �Ȃ̂œ����������́A
�Ȃ̂œ����������́A
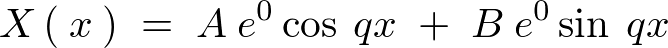
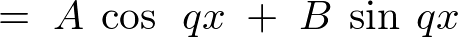
�ƂȂ�A����ɏ�������A
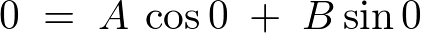
���A
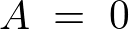
����ɁA
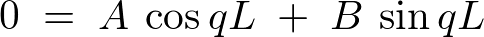
���A
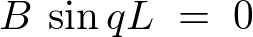
������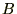 �ɂ��čl�@���Ă݂�ƁA���̂Ƃ�
�ɂ��čl�@���Ă݂�ƁA���̂Ƃ�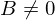 ��
��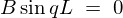 �̎������藧���߂ɂ�
�̎������藧���߂ɂ�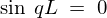 �łȂ���Ȃ�܂���B
�łȂ���Ȃ�܂���B
���̏����Ƃ̓T�C���̐����ɂ��A
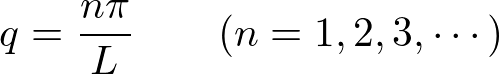
�łȂ���Ȃ�Ȃ��Ƃ������Ƃ��킩��܂��B
���̌��ʁA��������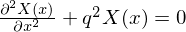 �̉��́A
�̉��́A
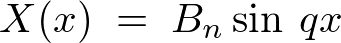
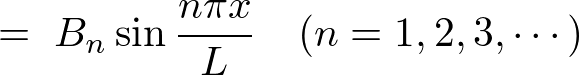
�ƂȂ�A
����ɂ��̂Ƃ��A
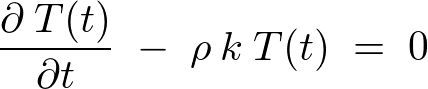
�̎��́A
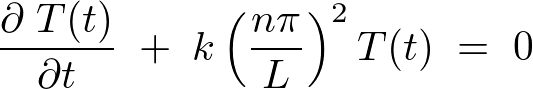
�����Ŏ������₷�����邽�߂�
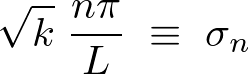
�ƒu���܂��B
����ƁA
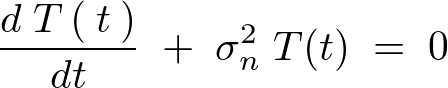
�������������łĂ����̂ł���������A
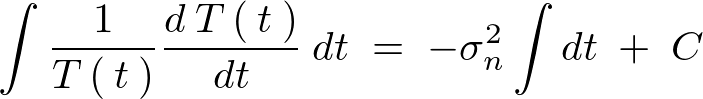
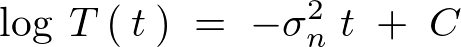
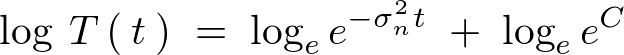
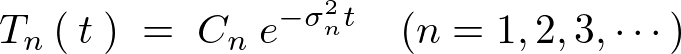
������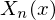 ��
��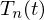 �̒萔���ꏏ�ɂ���A
�̒萔���ꏏ�ɂ���A
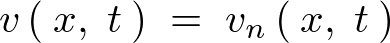
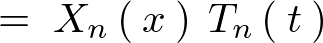
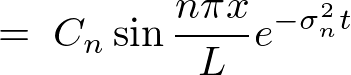
������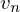 �̏d�ˍ��킹�i���`�����j���l���A�������������悤�ɂ���ƁA
�̏d�ˍ��킹�i���`�����j���l���A�������������悤�ɂ���ƁA
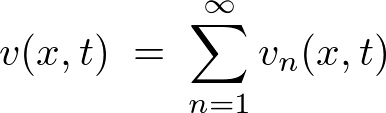
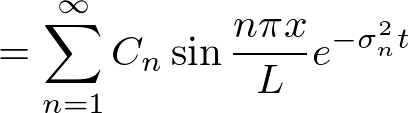
����ɂ́A
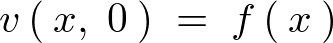
�Ƃ��������ɂ��A
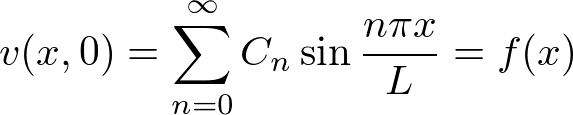
�����Ŕ���Ԃ̃t�[���G�����������v���o���ƁA
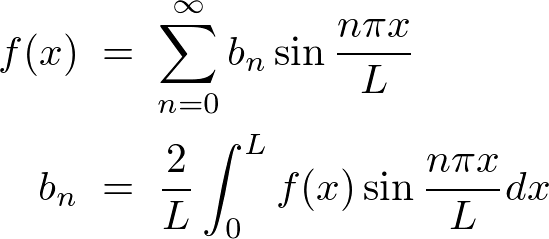
�Ƃ����̂��������̂ł�����g����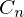 �͎��̂悤�ɕ\���ł��܂��B
�͎��̂悤�ɕ\���ł��܂��B
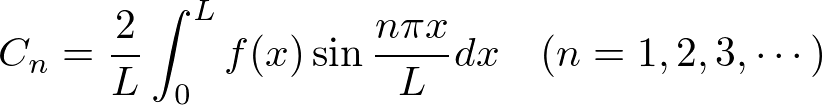
����ċ��߂���͎��̂悤�ɂȂ�܂��B
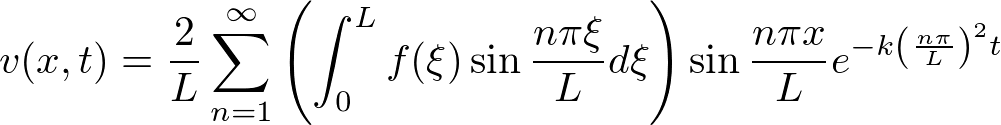
�ȏ�̂��Ƃ܂����̈ꎟ���M�`���������̎��ۂ̃��f�����v�Z���Ă݂܂��傤�B
�y���z
��������
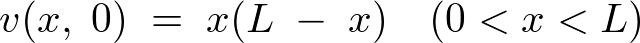
�ŁA
���E����
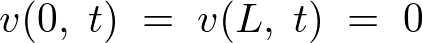
�y��@�菇�z
���̂Ƃ��A
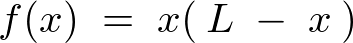
�Ȃ̂ŁA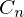 ��
��
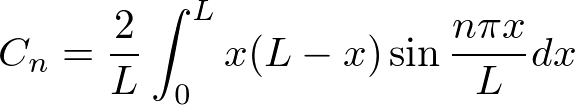
����������Ă����܂��B
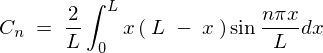
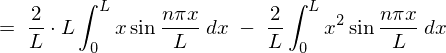
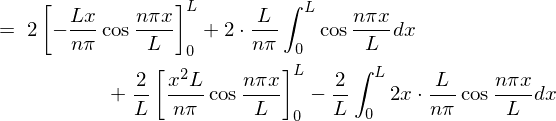

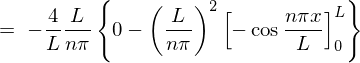
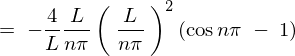
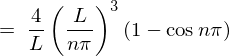
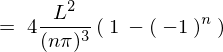
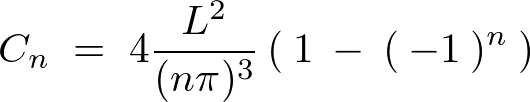
����� �̎��A
�̎��A
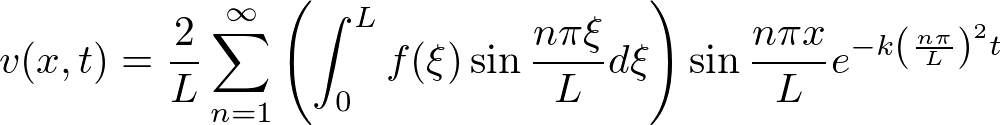
�ɑ������ƁA
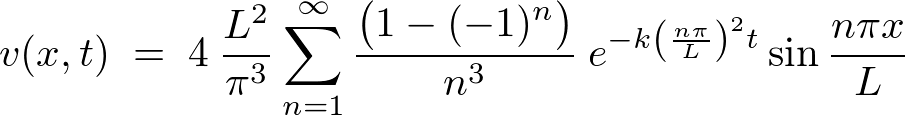
�y���z
���̂悤�ȔM�`���������A
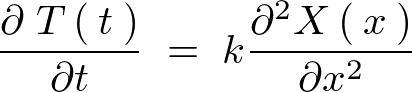
���A���Ɏ������������Ƌ��E�������݂����悤�����Ă݂܂��傤�B
- ��������
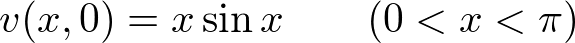
- ���E����
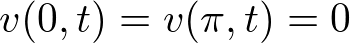
�y�����z
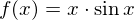 �Ȃ̂ŁA
�Ȃ̂ŁA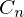 �́A
�́A
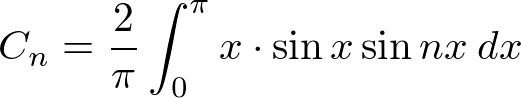
�����ŎO�p���̐����A
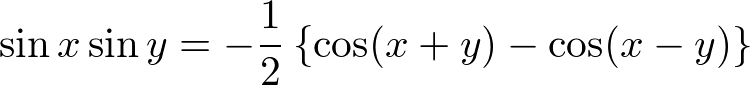
���g���A
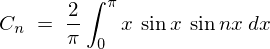
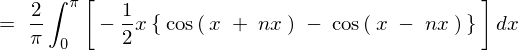
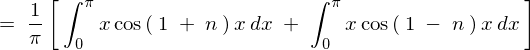
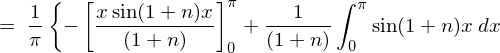
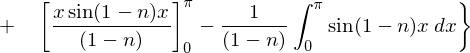
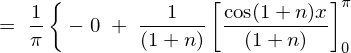
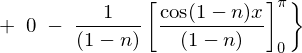
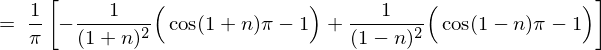
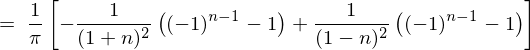
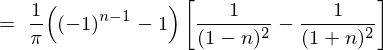
�㎮�̌��ʂ�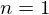 ���������
��������� �ɂȂ�Ǝv���܂��������Ő�قǂ̓r���̎��A
�ɂȂ�Ǝv���܂��������Ő�قǂ̓r���̎��A
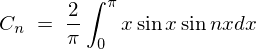
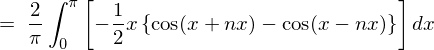

�ɂ����Ď��ۂ�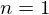 ��������Ƃǂ��Ȃ邩����Ă݂܂��傤�B
��������Ƃǂ��Ȃ邩����Ă݂܂��傤�B
��L�̉E�ӂ�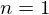 ��������ƁA
��������ƁA
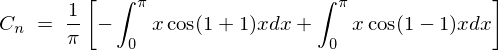
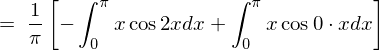
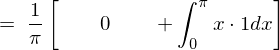
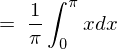
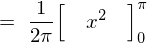
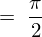
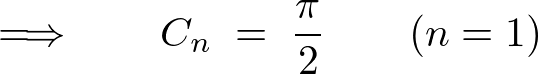
�M�`���������֘A�y�[�W
- ������Ԃɂ�����M�`��������
- �u���b�N�V���[���Y���f���Ƃ́A���Z�H�w�ɂ�����I�v�V�����̉��i����̍ۂɕK�v�Ȍv�Z���f���̂��Ƃ��w���܂��B���T�C�g�͂��̃u���b�N�V���[���Y�Δ����������̓��o�ߒ������ł͂Ȃ����������߂̏������w����J�ɉ�������T�C�g�ɂȂ�܂��B���̃`���v�^�[�ł͖�����Ԃɂ�����M�`���������̋��E�l���Ɋւ�����ɂ��čl�@���Ă����܂��B