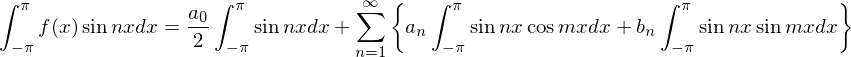�t�[���G�����W�J
���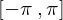 �͎��̂悤�a�̋L����p���ċ����ɓW�J���邱�Ƃ��\�ł���Ƃ��܂��B
�͎��̂悤�a�̋L����p���ċ����ɓW�J���邱�Ƃ��\�ł���Ƃ��܂��B
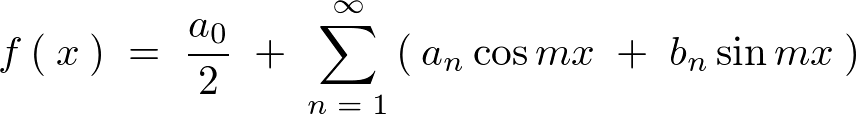
���̂悤�ɕ\�������Ƃ��A�㎮�̉E�ӁA
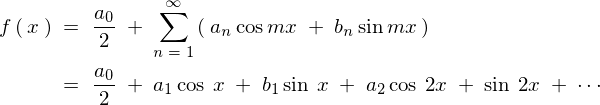
�̕������t�[���G�����W�J�Ƃ����܂��B
�E�ӎ�����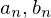 �͎��̂悤�ɂȂ�܂��B
�͎��̂悤�ɂȂ�܂��B
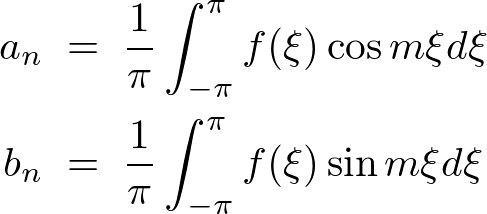
���ۂ�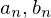 �����߂܂��B
�����߂܂��B
�܂��A
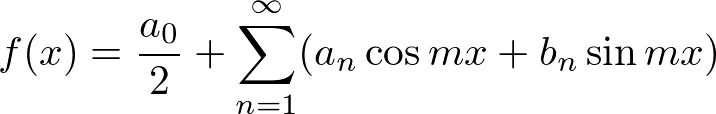
�̗��ӂ�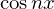 �������āA�����
�������āA�����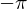 ����
����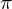 �܂ł�ϕ����Ă݂܂��B
�܂ł�ϕ����Ă݂܂��B
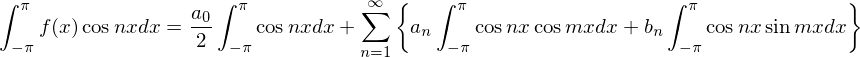
���E�ӑ�ꍀ�̌v�Z
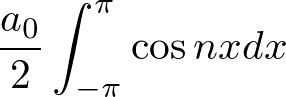
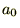 �Ȃ̂�
�Ȃ̂�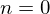 �ɂȂ�܂��B
�ɂȂ�܂��B
���������āA
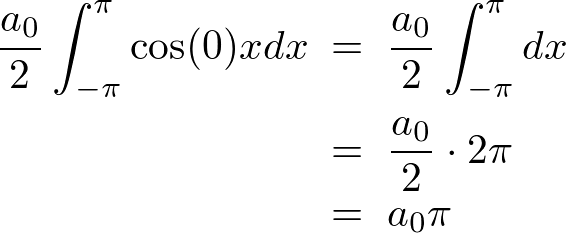
�E�ӑ�2���A3���̓��o
����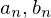 �̓��o�ł������̑O�ɎO�p���̐����ɂ��Ă����炢���Ă݂܂��傤�B
�̓��o�ł������̑O�ɎO�p���̐����ɂ��Ă����炢���Ă݂܂��傤�B
�O�p���̉��@�藝�ɂ͈ȉ��̐���������܂��B
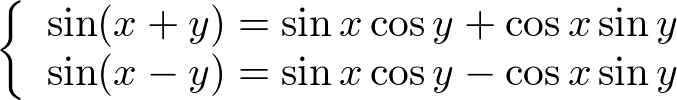
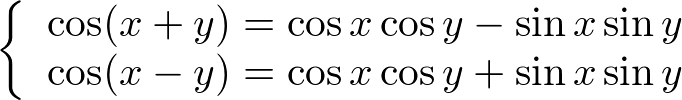
��L�̎����o����R�c�́A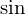 �̂ق��́g�V���R�X�R�b�V���h�A
�̂ق��́g�V���R�X�R�b�V���h�A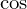 �̂ق��́g�R�X�R�X�V���V���h�A�ȂǂƂ���Ɗo���₷���ł��B
�̂ق��́g�R�X�R�X�V���V���h�A�ȂǂƂ���Ɗo���₷���ł��B
������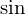 �̏ꍇ�͕����͂��̂܂܂ŁA
�̏ꍇ�͕����͂��̂܂܂ŁA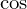 �̂ق��͕������t�ɂȂ�Ƃ������Ƃɒ��ӂ��܂��傤�B
�̂ق��͕������t�ɂȂ�Ƃ������Ƃɒ��ӂ��܂��傤�B
���̎��ɂ����āA�݂��Ɉ����Z�����Z�Ȃǂ�����Ƃ���Ɏ��̂悤�Ȏ���������܂��B
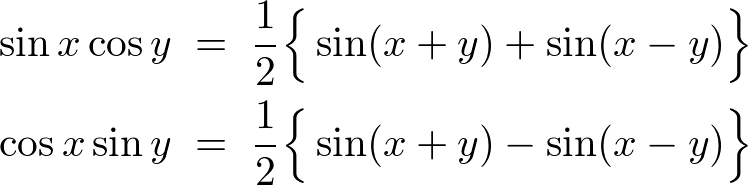
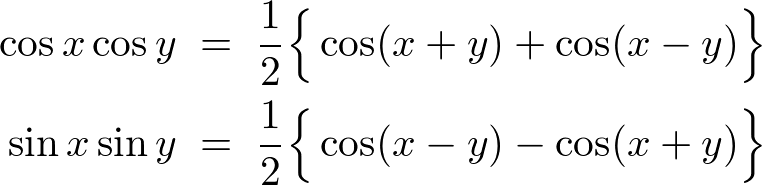
���������������������ď�L�̐ϕ��������Ă����܂��B
�E�ӑ�2���̌v�Z
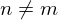 �̂Ƃ�
�̂Ƃ�
�܂��A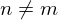 �̂Ƃ��A
�̂Ƃ��A
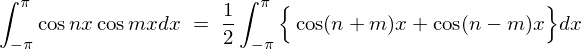
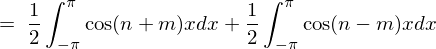
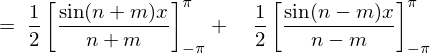

���j20211103���M�C���B�Ō�̌��ʂ�=0�������Ă��܂����B���������l�ѐ\���グ�܂��B
�Ȃ��A��L�̎��ɂ����Ă͎O�p���̐����ɂ����鎟�̂悤�ȊW���A
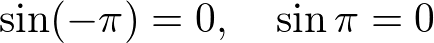
���g���Ă��܂��B
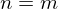 �̂Ƃ�
�̂Ƃ�
����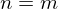 �ł���Ȃ�A
�ł���Ȃ�A
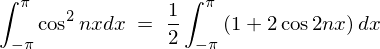
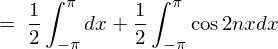
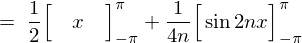
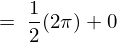

�Ƃ������ʂɂ��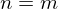 �̏ꍇ�͎��̂悤�Ȍ��ʂɂȂ�܂��B
�̏ꍇ�͎��̂悤�Ȍ��ʂɂȂ�܂��B
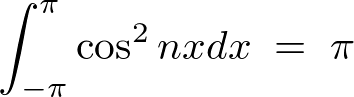
���̂Ƃ����̌��ʂɂ��A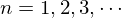 �̂Ƃ��A
�̂Ƃ��A
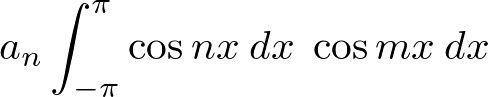
��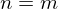 �̂Ƃ������[���łȂ����ʂ��o�܂��B
�̂Ƃ������[���łȂ����ʂ��o�܂��B
����āA

�̏ꍇ�A
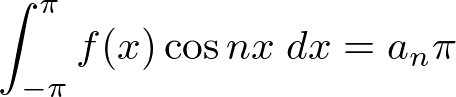
�ɂ��ȉ��̂悤�ɋ��܂�܂��B
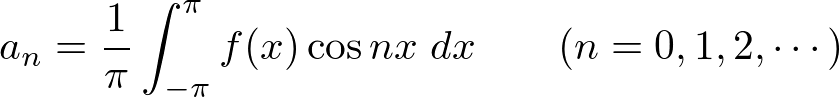
�E�ӑ�3���̌v�Z
�����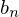 �̕����́A
�̕����́A
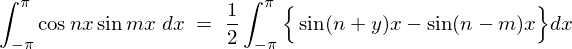
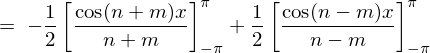
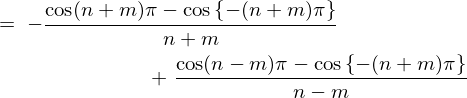
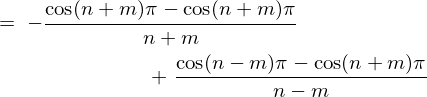

�ƂȂ�̂Ō��ʂ̓[���B
�܂��A�R�T�C���̋���ɂ��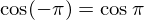 �ł��B
�ł��B
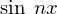 ���������ꍇ
���������ꍇ
���ɁA
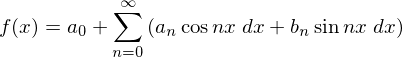
�̗��ӂ�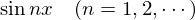 �������āA
�������āA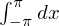 ���܂��B
���܂��B
��L���E�ӑ�ꍀ�́A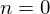 �Ȃ̂Ŏ����̂������ł��܂��B
�Ȃ̂Ŏ����̂������ł��܂��B
����ɑ�Q�����A��قǂ̏�L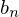 ���̂悤�Ɍv�Z���Ă����Γ����悤�Ɍ��ʂ͂O�ɂȂ�܂��B
���̂悤�Ɍv�Z���Ă����Γ����悤�Ɍ��ʂ͂O�ɂȂ�܂��B
�E�ӑ�3���̌v�Z
��R��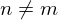 �̂Ƃ�
�̂Ƃ�
����ɑ�3���Ɋւ��Čv�Z���Ă����܂��B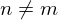 �̂Ƃ��B
�̂Ƃ��B
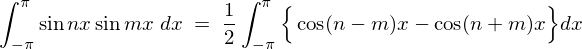
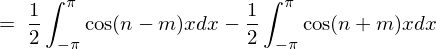
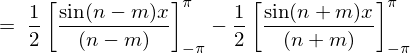

���j20211103���M�C���B�Ō��=0�̎�������܂���ł����B���������l�ѐ\���グ�܂��B
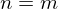 �̂Ƃ�
�̂Ƃ�
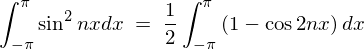
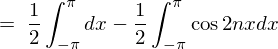
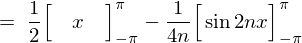
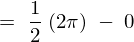

�ƂȂ�̂Ō��ʂ͎��̂悤�ɂȂ�܂��B
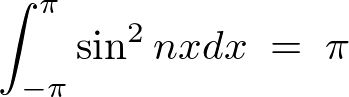
���̌��ʂɂ��A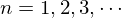 �̂Ƃ��A
�̂Ƃ��A
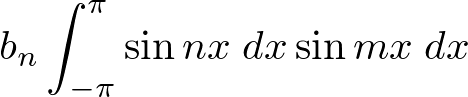
��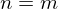 �̂Ƃ������[���łȂ����ʂ��o�܂��B
�̂Ƃ������[���łȂ����ʂ��o�܂��B

�ƂȂ�̂ŁA
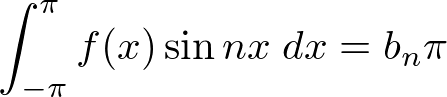
���A
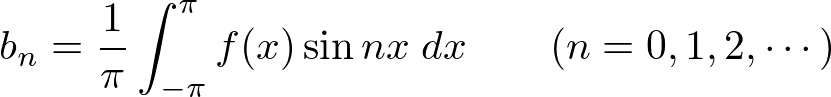
�Ƃ������ʂ����ꂼ�ꓱ����܂��B
�ȏ�̌��ʂ��A�t�[���G�����W�J�̎��́A
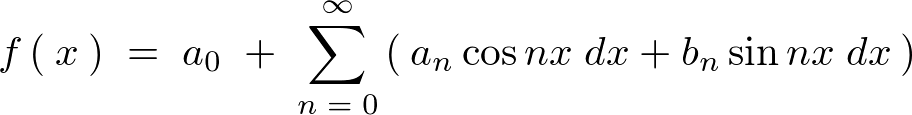
�Ə����邱�Ƃ��킩��܂��B
����̓I�ȗ�
���Ɏ����͈͂�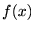 ���t�[���G�����W�J���Ă݂܂��傤�B
���t�[���G�����W�J���Ă݂܂��傤�B
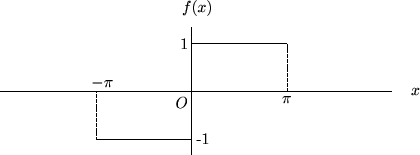
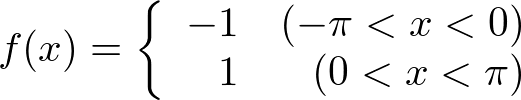
�܂����߂���̂�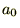 ��
��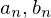 �ł��B
�ł��B
�܂�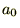 ���v�Z���܂��B
���v�Z���܂��B
��1���̌v�Z
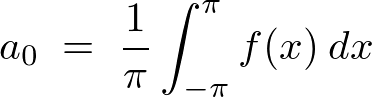
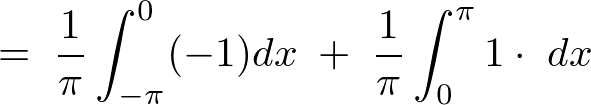
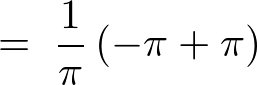
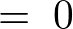
�Â��đ�Q��R���̌v�Z�����܂��B
��2���̌v�Z
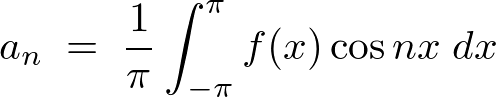
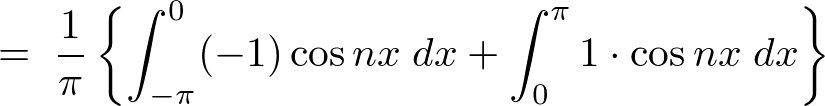
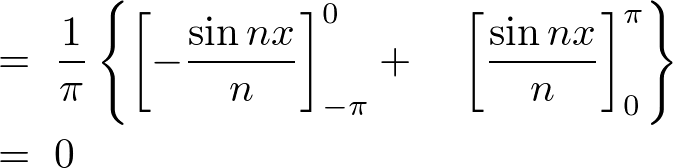
��3���̌v�Z
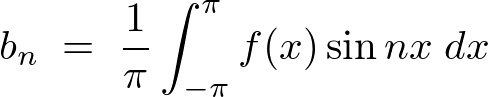
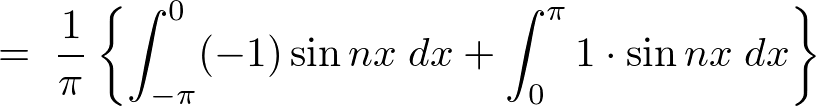
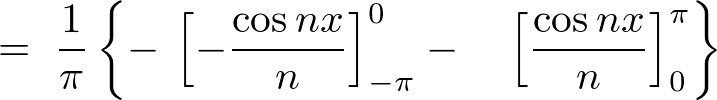
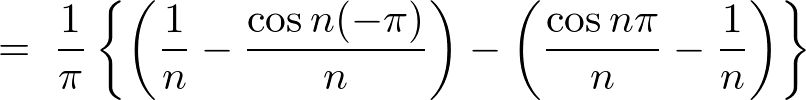
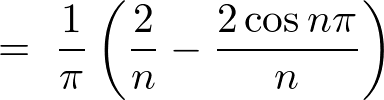
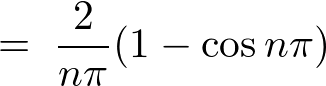
�����̌��ʂɂ���3����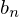 �݂̂��Ӗ��̂�����ɂȂ�܂��B
�݂̂��Ӗ��̂�����ɂȂ�܂��B
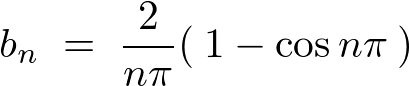
�\��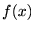 �̃t�[���G�����W�J�̎��ɏ�L�̌��ʂ����Ă͂߂čs���Ĉȉ��̂悤�Ɍv�Z���Ă����܂��B
�̃t�[���G�����W�J�̎��ɏ�L�̌��ʂ����Ă͂߂čs���Ĉȉ��̂悤�Ɍv�Z���Ă����܂��B
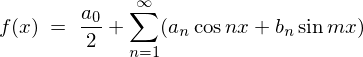
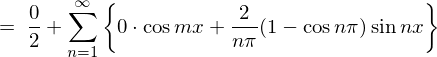
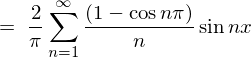
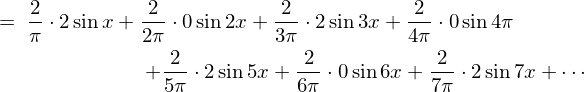
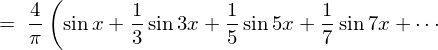
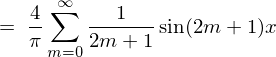
���̌��ʂɂ��ȉ��̂悤�Ȍv�Z���ʂ܂��B
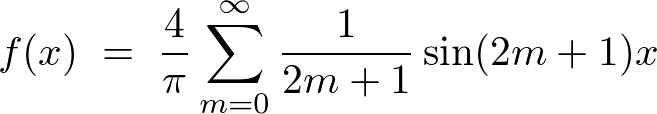
���ɒP���Ɏ����� �A
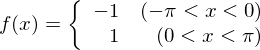
�̂悤�ȃ��f������Ȃ���L�̂悤�Ȏ����o�Ă���̂��ƍl�����ޕ��������Ǝv���܂����A�܂������͂��܂�[���l�����ɂ����������̂Ȃƌy���~�߂܂��傤�B
�t�[���G�����W�J�֘A�y�[�W
- �t�[���G�����W�J�E�]���W�J
- �u���b�N�V���[���Y���f���Ƃ́A���Z�H�w�ɂ�����I�v�V�����̉��i����̍ۂɕK�v�Ȍv�Z���f���̂��Ƃ��w���܂��B���̃`���v�^�[�ł̓u���b�N�V���[���Y���f���Δ����������ӂ��ߒ��ɂ����ďd�v�ɂȂ�t�[���G��͂Ɋւ��ĉ�����Ă����܂��B
- �t�[���G�ϕ�
- �u���b�N�V���[���Y���f���Ƃ́A���Z�H�w�ɂ�����I�v�V�����̉��i����̍ۂɕK�v�Ȍv�Z���f���̂��Ƃ��w���܂��B���̃`���v�^�[�ł̓u���b�N�V���[���Y���f���Δ����������ӂ��ߒ��ɂ����ďd�v�ɂȂ�t�[���G��͂Ɋւ��ĉ�����Ă����܂��B