��W���Q�K��������������
����������
2�K�̂�������������A
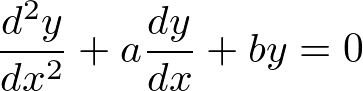
���l���Č��܂��傤�B
���܁A���ɂ��̎���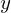 ��
��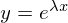 �����ł���Ƃ��܂��B
�����ł���Ƃ��܂��B
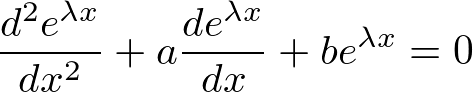
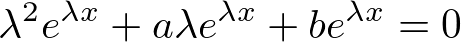
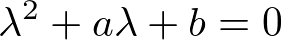
���������������Ƃ����܂��B
�����ō��Z�ŏK�������̌�����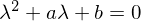 ���g���Ă݂�ƁA
���g���Ă݂�ƁA
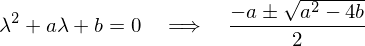
���ʖ@�Ƃ����̂��o���Ă݂��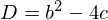 �ł�������ɂ���ĉ��̎�ނ�3��ނقǂɕ��ʂł��܂��B
�ł�������ɂ���ĉ��̎�ނ�3��ނقǂɕ��ʂł��܂��B
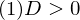 �̂Ƃ�
�̂Ƃ�
���͈قȂ�Q�̎����̉�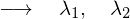 �ƂȂ�A��{���́A
�ƂȂ�A��{���́A

����Ɉ�ʉ��́A
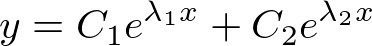
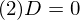 �̂Ƃ��i�d���ƌĂ�
�̂Ƃ��i�d���ƌĂ�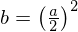 �̂Ƃ��ɋN����܂��j
�̂Ƃ��ɋN����܂��j
���͏d���ƂȂ�܂��B�@
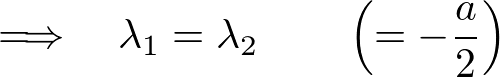
���̏ꍇ�A���̓����������̍���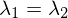 �ł����ȒP�Ɋ�{������������2�Ƃ������Ƃɂ͂Ȃ�܂���B
�ł����ȒP�Ɋ�{������������2�Ƃ������Ƃɂ͂Ȃ�܂���B
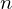 �K�̔����������ɂ�
�K�̔����������ɂ�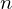 �̔C�Ӓ萔���܂�
�̔C�Ӓ萔���܂�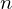 �̉����K�v�ł��B
�̉����K�v�ł��B
�܂�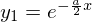 �ɑ��Đ��`�Ɨ��Ȃ�����̉������߂Ȃ���Ȃ�܂���B
�ɑ��Đ��`�Ɨ��Ȃ�����̉������߂Ȃ���Ȃ�܂���B
����2�ڂ̉������ɁA
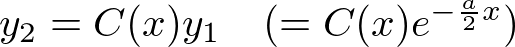
�ƒu���܂��B
�����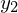 �́A
�́A
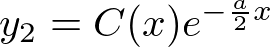
�ƂȂ�܂��B
������A
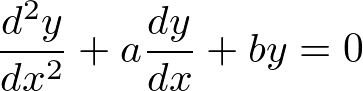
�ɑ�����Ă݂�ƁA
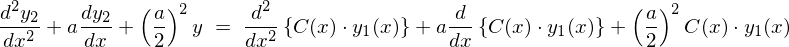
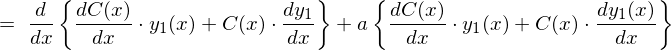
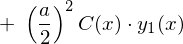
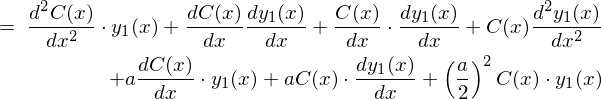
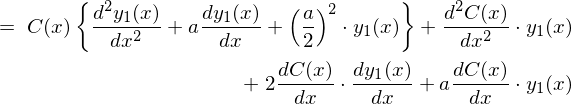
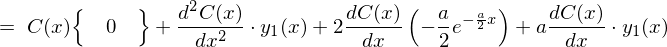
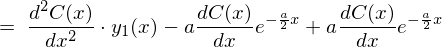
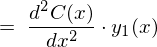
�ɂȂ�̂ŏ�L��2�K�����������͎��̂悤�ɂȂ�܂��B
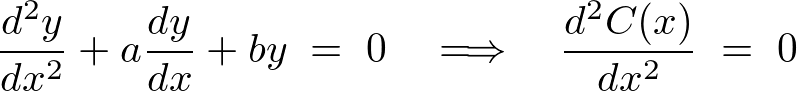
����ɍ��x�͂��̂łĂ��������Q��ϕ����܂��B
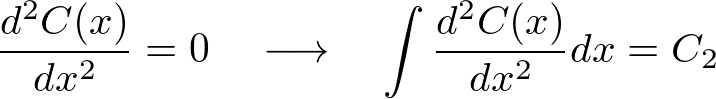
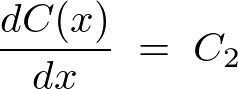
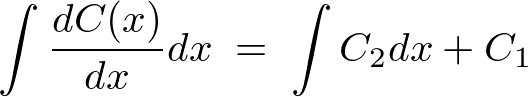
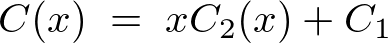
�����ɂ��A
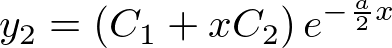
�ƂȂ�܂����A�����ł��Ƃ߂Ă���̂�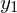 �Ƃ͈Ⴄ�Ɨ��ȉ������߂邱�ƂȂ̂ł����P�ɁA
�Ƃ͈Ⴄ�Ɨ��ȉ������߂邱�ƂȂ̂ł����P�ɁA
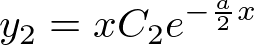
�ƒu���܂��B
��������ƁA
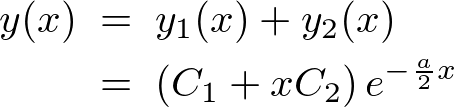
�ƂȂ�܂��B
������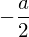 �����̂悤�ɒu���܂��B
�����̂悤�ɒu���܂��B
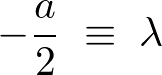
��������Ɗ�{���́A

��ʉ��͈ȉ��̂悤�ɂȂ�܂��B
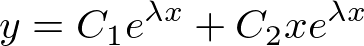
(3)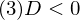 �̂Ƃ�
�̂Ƃ�
���̂Ƃ����͎����Ƃ���ȊO�ɋ����ƌĂ����̂��~�b�N�X���ꂽ���f�����ƌĂ����̂ɂȂ�܂��B
�ėp�u���b�N�V���[���Y���f�����ۂɂ͂��̂Ƃ��̉���p���܂��B
���́A

�Ƃ��������̂ɂȂ�A��{���͎��̂悤�ɂȂ�܂��B
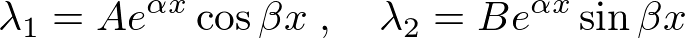
������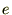 �ɑΉ�����������
�ɑΉ����������� �Ƃ������O�p���̂ق��ɑΉ����Ă��܂��B
�Ƃ������O�p���̂ق��ɑΉ����Ă��܂��B
�����������͎��̂悤�ɂȂ�܂��B
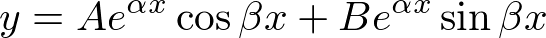
���Ȃ݂ɋ���$i$��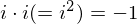 �Ƃ����������������Ă��܂��B
�Ƃ����������������Ă��܂��B
�y���z
���Ɏ����������������Ă݂܂��傤�B
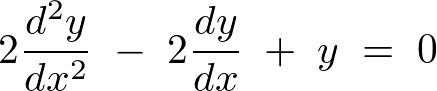
�y�����z
�܂����������������܂��B
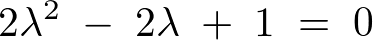
�����������o���Ȃ��̂ł���͉��̌������g���ċ��߂܂��B
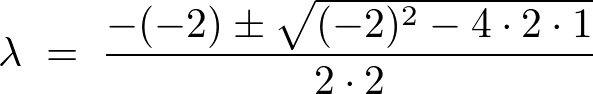
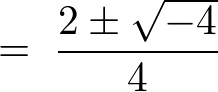
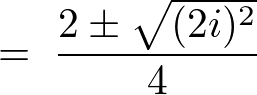
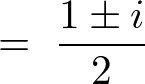
�ƂȂ�̂Ŋ�{���́A
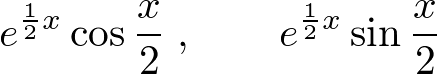
�ƂȂ�̂ň�ʉ��͎��̂悤�ɂȂ�܂��B
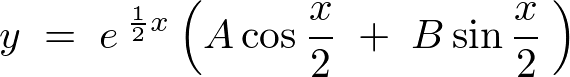
��W���Q�K���������������֘A�y�[�W
- �����������
- �u���b�N�V���[���Y���f���Ƃ́A���Z�H�w�ɂ�����I�v�V�������i����̍ۂɕK�v�Ȍv�Z���f���̂��Ƃ��w���܂��B���T�C�g�͂��̃u���b�N�V���[���Y���f���Δ����������̓��o�ߒ������ł͂Ȃ����������߂̏������w����J�ɉ�������T�C�g�ł��B���̃`���v�^�[�ł͂��̃u���b�N�V���[���Y�Δ��������������߂̔������������ȒP�ɂ܂Ƃ߂Ă���܂��B�����������Ƃ����̂́A���̎��̒��ɓƗ��ϐ��Ƃ��̊��A����т��̓��������܂�ł�����̂������܂��B���̔����������������Ƃ����̂͗^�����Ă��鎮���P���I�ɖ��������̂����߂邱�Ƃł���A���̉��ɂ͈�ʉ��ƁA����ɂ͔C�Ӓ萔�ɓ��ʂȒl�����ċ��߂������Ȃǂ�����܂��B ������������Ƃ͂���ϐ��ɑ�����Ƃ���1�K�A2�K�`�Ȃǂ̓����ƁA����Ɨ��ϐ����܂������ɂȂ肻�̓Ɨ��ϐ���1�̂��̂������܂��B


























