�����������
�����������̗�1�j
���̂悤�� �Ɋւ�����������l���܂��B
�Ɋւ�����������l���܂��B
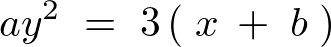
������ �ɑ��Ĕ������܂��B
�ɑ��Ĕ������܂��B
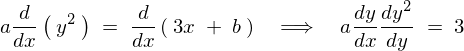
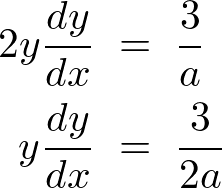
���������ɔ�������ƁA
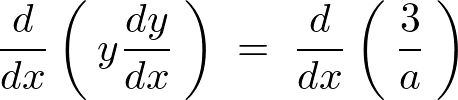
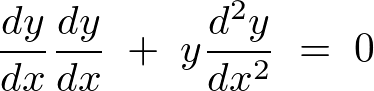
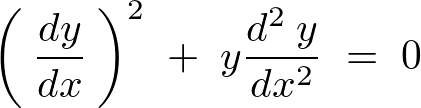
�Ƃ��������̂������������ł��B
���j20211023�C��(�v�Z�ߒ��y�ь��ʂ��Ԉ���Ă���܂����B�����f����������������ϐ\�������܂���ł���)
�����������̗�2)
���̉~�ɂ��čl�@���Ă݂܂��傤�B
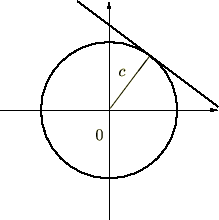
���̉~�Ɋւ��Ă̕�������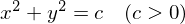 �������Ǝv���܂��B
�������Ǝv���܂��B
����� �Ŕ�������Ƃǂ��Ȃ�ł��傤���H
�Ŕ�������Ƃǂ��Ȃ�ł��傤���H
���ۂɂ���Ă݂�ƁA
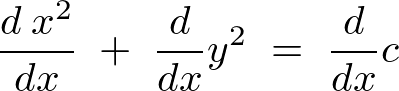
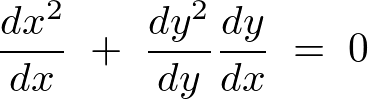
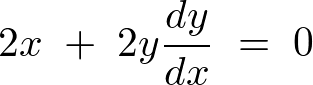
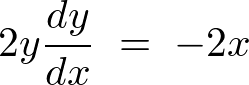
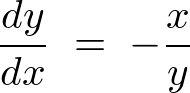
�Ƃ��������o�Ă��܂��B
����͉~�̐ڐ������̌X�����Ӗ����Ă��܂��B
�y���K�����������̉��z
�����������Ɋ܂܂�铱���̊K���i�h�b�g���j�̈�ԍ������́i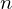 �K�j���A
�K�j���A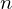 �K�̔����������Ƃ����܂��B �����������̉��ɂ͈�ʉ��Ɠ�����Ƃ����̂�����܂��B��{�I�ɂ�
�K�̔����������Ƃ����܂��B �����������̉��ɂ͈�ʉ��Ɠ�����Ƃ����̂�����܂��B��{�I�ɂ�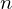 �K�����������ɂ�
�K�����������ɂ�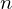 �̔C�Ӓ萔���܂�
�̔C�Ӓ萔���܂�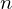 �̈�ʉ�������A����ɂ͂��̔C�Ӓ萔
�̈�ʉ�������A����ɂ͂��̔C�Ӓ萔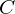 �ɂ����ď��������Ȃǂ����Ă��Ă��̏����̂��Ƃł������܂�Ȃ����c�����������Ƃ�����̂�����܂��B
�ɂ����ď��������Ȃǂ����Ă��Ă��̏����̂��Ƃł������܂�Ȃ����c�����������Ƃ�����̂�����܂��B
�y���z
���̔��������������߁A�����Ă��̈�ʉ����� ���̏�������������������Ă݂܂��傤�B
���̏�������������������Ă݂܂��傤�B
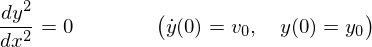
�y�����z
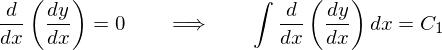
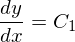
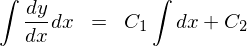
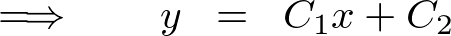
���ꂪ���߂��ʉ��ɂȂ�܂��B
����ɂ��̈�ʉ��ɑ��ď�����������������������߂܂��B
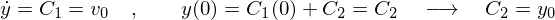
�Ȃ̂ŋ��߂������́A
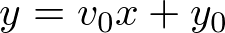
�ƂȂ�܂��B
�y1�K����������(�ϐ������`)�z
���̌`�̔������������l�@���Ă݂܂��傤�B
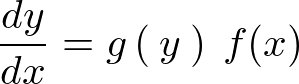
�������Ƃ��ẮA�܂��ϐ����Q����̂ŗ��ӂɂ��ꂼ����g������h�Ƃ������Ƃ����܂��B

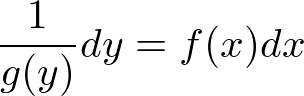
���ɂ��̎��̗��ӂ����ꂼ��ϕ����܂��B
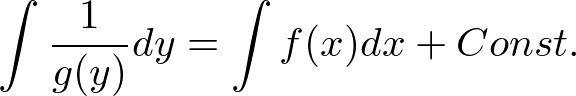
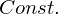 �Ƃ��̂͐ϕ��萔�ł��B
�Ƃ��̂͐ϕ��萔�ł��B
���j20211026�C���B�����Ԉ���Ă���܂����B��ϐ\�������܂���ł����B
�y���z
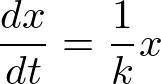
�܂��ϐ������Ƃ�����Ƃ����A���ꂼ���ϕ����čs���܂��B
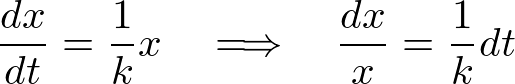
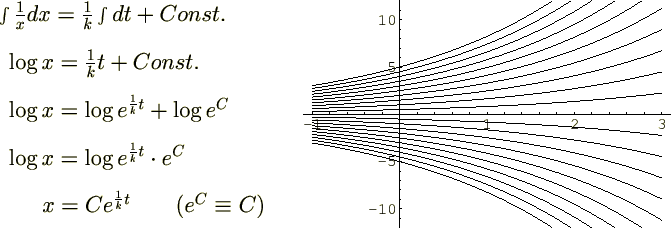
�E��}��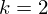 �̂Ƃ���
�̂Ƃ���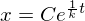 �A�܂�
�A�܂�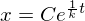 ���O���t���������̂ł��B
���O���t���������̂ł��B
���C���������ɕ�����Ă��闝�R�͌v�Z�ɂ���ďo�Ă����ϕ��萔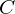 �̒l��
�̒l��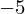 ����
����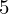 �͈̔͂�
�͈̔͂�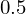 ���݂Ńv���b�g���Ă��邽�߂ł��B
���݂Ńv���b�g���Ă��邽�߂ł��B
�y���z
���̔����������������Ă݂Ă��������B
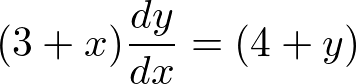
�y�����z
�܂��ό`�����܂��B
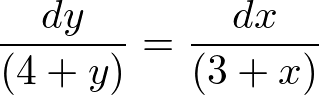
���ɗ��ӂ�ϕ����܂��B
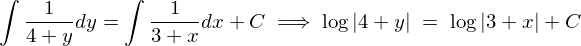
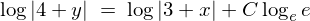
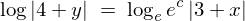
���ӂ̑ΐ����Ƃ��āA
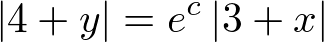
���ꂪ���߂��ʉ��ɂȂ�܂��B
������������֘A�y�[�W
- ��W���Q�K��������������
- �u���̃y�[�W�ł͂a�r���f�����o�̍ۂɂ����ĕK�v�ɂȂ�����������̊T�O�Ƃ��̐����ɂ��ĉ�����Ă����܂��B��W���Q�K���������������ɂ����Ă͂܂���{����O��ɂ�������������������A�����Ĕ��ʖ@���g�������̎�ނ��R�قǏo���Ă��ꂼ��̈�ʉ����Ă����܂��B�u���b�N�V���[���Y���f���Ƃ́A���Z�h�����i����舵���ۂɂ����āA���̗��_�I���i�����肷��ۂɕ��L���p�����Ă��鐔�����f���̂��Ƃ��w���܂��B���T�C�g�ł͂��̃u���b�N�V���[���Y���f���o����ꍇ�ɗp�����鐔���v�Z�ߒ��݂̂Ȃ炸�A���̓��o�̑O��ɍŒ���K�v�ɂȂ�����ϕ��Ȃǂ̊�{�I�Ȑ��w�������������T�C�g�ɂȂ��Ă���A���n�o�g�̕��̗����̏����ɂȂ�悤�Ȃ�ׂ����ݍ�����������悤�S�|��������ɂȂ��Ă��܂��B


























