�d���C�w���p�̊ȒP�ȗ�
�q�n�s�̌v�Z
�����Ȃ̈�N���ɏK���x�N�g����͂ł̃��[�e�[�V�����v�Z�Ɋւ��Ă̋L�q�͂قƂ�ǂ̏ꍇ�R�s�R��̍s�ɕ\�L���Ă��邩�Ǝv���܂��B
�����Ă��̏ꍇ�A���ۂ̌v�Z�ł̓T���X�ʼn��������邢�͍s��\�L�ł͂Ȃ����̌����̂悤�Ȃ��́i���j��������Ă���̂��嗬���Ǝv���܂��B
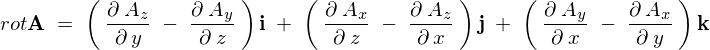
�����������̂͊o����̂ɑ�ϋ�J����̂ŁA���̃��[�e�[�V�����v�Z�Ɋւ���s���X�J���[�O�d�ς̃Z�N�V�����ɂ����ďo�Ă����w�s�W�J�@�x���g���Ă���Ă݂邱�Ƃɂ��܂��傤�B
�y���̕ό`�z
���[�e�[�V�����̍s�̕\�L�͂��̂悤�������Ǝv���܂��B
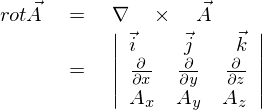
������X�J���[�O�d�ς̃Z�N�V�����ɂ����Ă�����z�u�������悤�Ɏ{���܂��B
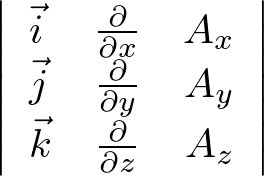
�̂悤�ɂ��܂��B
������s�W�J�@�ɂ���Ď��̂悤�Ɍv�Z���Ă����܂��B
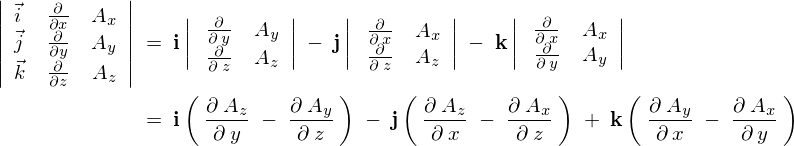
�����ʼnE�ӑ�2���̒��̕Δ��������ւ��i������ω��j�A��{�x�N�g���̈ʒu����L�\�L�ʂ�ɂ���Ό��ǂ̂Ƃ��뎟�̂悤�ɂȂ�܂��B
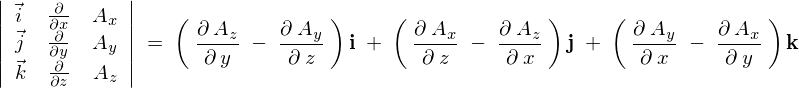
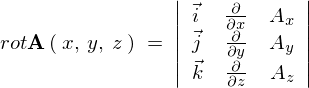
�דd���q�̉^��������
���̋���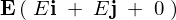 �̓d��Ɏ������x
�̓d��Ɏ������x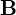 �̈��̋����̎��ꂪ
�̈��̋����̎��ꂪ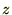 �����ɂ������Ă���Ƃ��܂��B
�����ɂ������Ă���Ƃ��܂��B
���̍��W�n�ɂ����Ẳדd���q�̉^�������������߂Ă݂܂��傤�B
�܂��A�l���Ă�����W�n�ɂ����Ă̓d��Ǝ���̂��ꂼ��R�����̐��������̂悤�Ȃ��̂Ƃ��܂��B
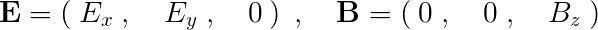
�N�[�����͂�����Ƃ��̃��[�����c�͎͂��̂悤�ɕ\����܂��B
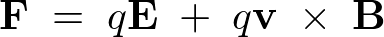
�E�ӑ�Q��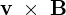 ���v�Z����ƁA
���v�Z����ƁA
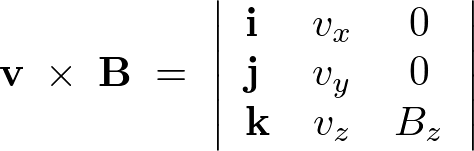
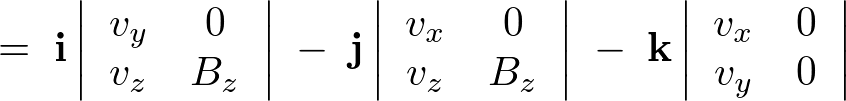
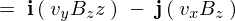
���[�����c�̎��ɑ�����܂��B
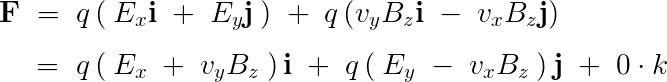
����Ƀx�N�g��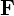 ���A
���A
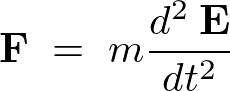
�ł���Ȃ�A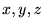 �̂��ꂼ��̕����ɑ��Ď��̂悤�ɂȂ�܂��B
�̂��ꂼ��̕����ɑ��Ď��̂悤�ɂȂ�܂��B
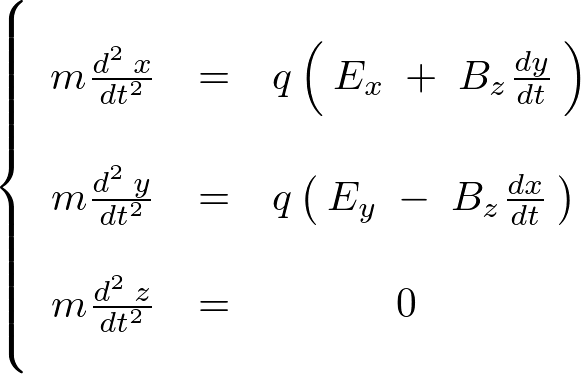
�d���C�w�ւ̉��p�֘A�y�[�W
- ���̑��d�v�Ȑ���
- ���T�C�g�͎�ɕ����Ɋւ��鐔�w�ȂǁA���̑����ӂ��܂߂����X�������ς̃E�F�u�T�C�g�ł��B ���w����Ɋւ��Ă̎�|�Ƃ��ẮA�ʏ�̃e�L�X�g�ł͊�������Ă��܂����e�Ȃǂ��ڂ����L�q���A����ɂ͓������������̂ł͂Ȃ��A�킩��ɂ������e�������ɂ킩��₷���`���邩���ȂǁA�����������E�F�u�R���e���c�Ȃ�ł̗͂����Ƌ@�����������T�C�g�쐬�����Ƃ��Ă��܂��B
- �}�e�}�e�J�ɂ��x�N�g���`��
- �}�e�}�e�J�ɂ��x�N�g���\�����Q�����ƂR�����ɂ���ĕ`�悷����@�̐����B


























