重回帰分析
yを目的変数として説明変数をxとしたとき重回帰モデルの式は以下のように表される。
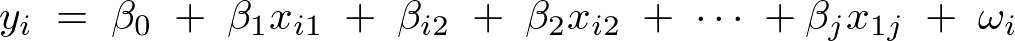
単回帰モデルの説明変数が一つなのに対しこの重回帰モデルは説明変数を2つ以上をとる。一つの目的変数を複数の説明変数によって相関関係により導く。
(※このページは左の書籍とデータ分析教室 Nava(ナバ)のサイトを参考にしております。特にナバ様の説明は大変参考になりました。ありがとうございます。)
ここでは大気汚染に関してのデータ”usair”というデータを使用し、目的変数をso2、その他のデータを説明変数として考える。
(※このページは左の書籍とデータ分析教室 Nava(ナバ)のサイトを参考にしております。特にナバ様の説明は大変参考になりました。ありがとうございます。)
usair
大気汚染データ
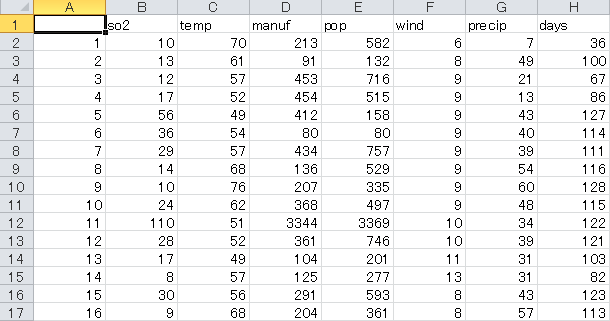
7つあるそれぞれの変数の意味は次のようになる。
| SO2 | 大気中の1立方メートル当たりのSO2(二酸化硫黄)の量 |
|---|---|
| Temp | 年間平均気温 |
| Manuf | 20人以上の従業員を雇用している製造業の数 |
| Pop | 千人単位での人口数 |
| Wind | 時間当たりの年平均風速(マイル) |
| Precip | 年間の平均降水量(インチ) |
| Day | 年間の平均降水日数 |
usair_csv <- read.csv("usair.csv")
データの上部分の確認
head(usair_csv)
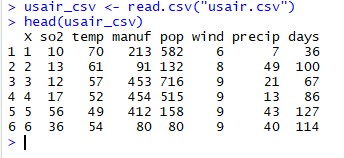
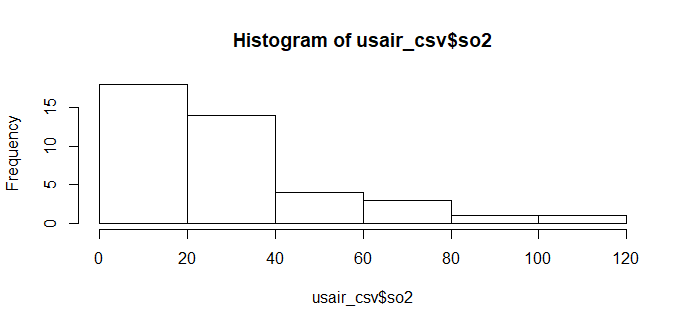
ヒストグラムによるデータの可視化
hist(usair_csv$so2)
hist(usair_csv$temp)
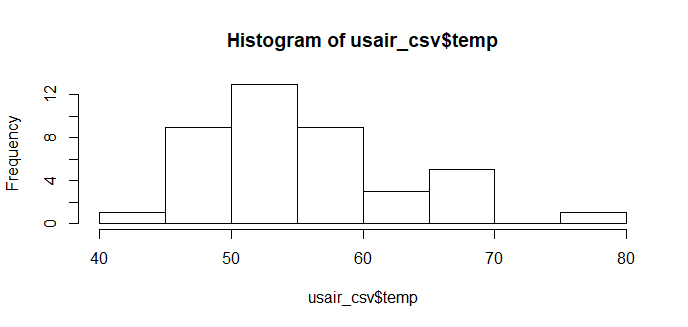
hist(usair_csv$manuf)
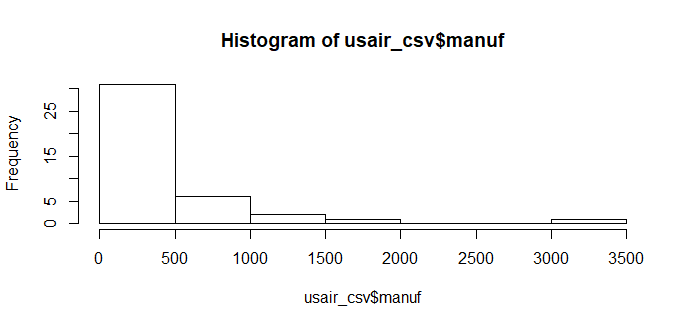
hist(usair_csv$pop)
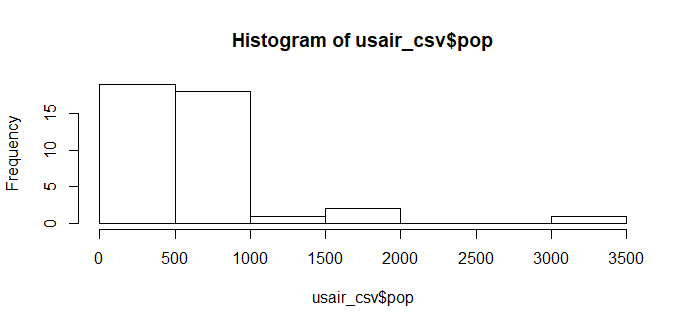
最初にデータを可視化することでデータの全体像を把握するのに役立つ。
相関分析
目的変数とそれぞれの説明変数との関係性の大きさを見るために相関係数と散布図の出力を行う。
相関係数と散布図を同時に表示するpsychというパッケージを使ってデータを可視化する。
psychのインストール
install.packages("psych")
ライブラリ読み込み
library(psych)
usair_csv.fit <- usair_csv[,c(2,3,4,5,6,7,8)]
psych::pairs.panels(usair_csv.fit)
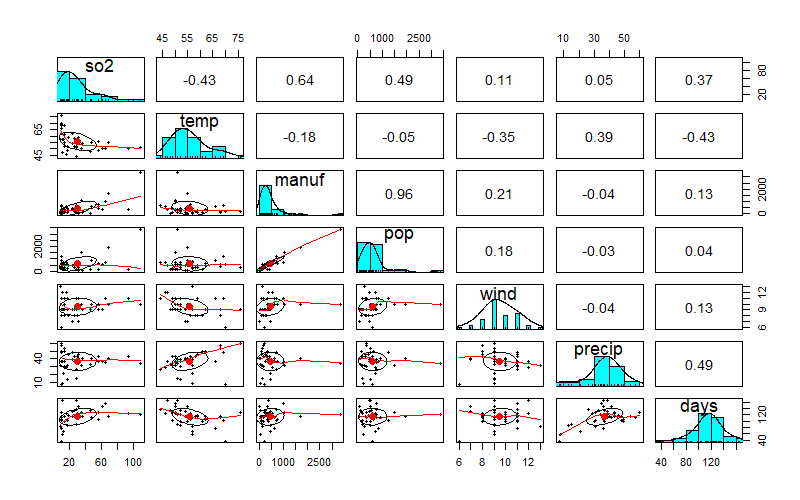
重回帰モデルの構築と要約
上の結果により目的変数のso2とその他変数の相関分析による関係性の強弱はわかったがひとまずすべての変数を使った重回帰分析と解析結果の要約を実行していく。
so2を目的変数とし残りの変数を説明変数として重回帰モデルで説明していく。 以下のように読み込ませ実行する。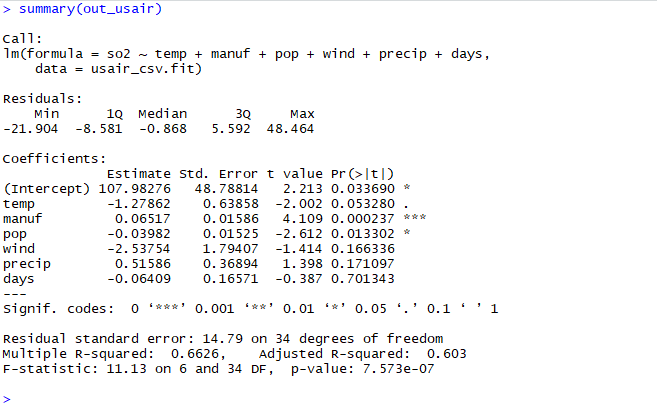
so2を目的変数とし残りの変数を説明変数として重回帰モデルで説明していく。 以下のように読み込ませ実行する。
out_usair <- lm(so2 ~ temp + manuf + pop + wind + precip + days, data = usair_csv.fit)

| 共変量 | 回帰係数の推定値 | 標準偏差 | t値 | p値 |
|---|---|---|---|---|
| Intercept | 107.98276 | 48.78814 | 2.213 | 0.033690 |
| temp | -1.27862 | 0.63858 | -2.002 | 0.053280 |
| manuf | 0.06517 | 0.01586 | 4.109 | 0.000237 |
| pop | -0.03982 | 0.01525 | -2.612 | 0.013302 |
| Wind | -2.53754 | 1.79407 | -1.414 | 0.166336 |
| precip | 0.51586 | 0.36894 | 1.398 | 0.171097 |
| days | -0.06409 | 0.16571 | -0.387 | 0.701343 |
上記の結果のcoefficientsの部分を見てみるとmanufとpopの2つが二酸化硫黄のレベルを予測するのに最も適しているのがわかる。また右に*印がついているのもmanufとぽpopでp値が小さいほど右に:*印がつき(最大で3つ)優位な説明変数だということがわかる。























