僥僀儔乕揥奐
懡崁幃偺揥奐
椺偊偽師偺傛偆側幃丄
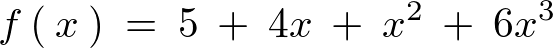
偙偺幃傪丄
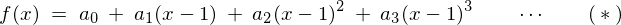
偲偄偭偨宍偵偡傞偙偲傪峫偊偰傒傑偡丅
傑偢丄幃傪師乆偵旝暘偟偰偄偔偲丄
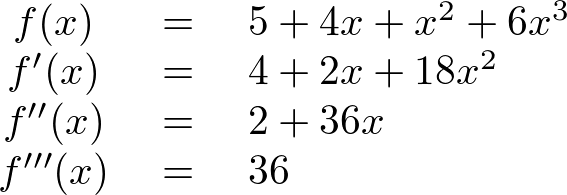
偙偙偱倶偵侾傪戙擖偟偰偄偔偲丄
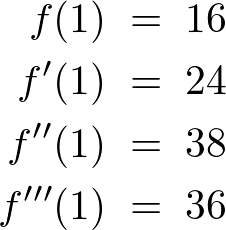
偲偄偆寢壥偑弌偰偒傑偡偑丄偙偙偱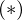 偺幃傪
偺幃傪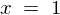 偲偍偔偲丄傑偢丄
偲偍偔偲丄傑偢丄
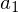 傪媮傔傞偨傔偵
傪媮傔傞偨傔偵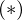 偺幃傪x偱旝暘偟丄侾傪戙擖偡傞偲丄
偺幃傪x偱旝暘偟丄侾傪戙擖偡傞偲丄
偪側傒偵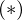 偺幃偺旝暘偼崌惉娭悢旝暘傪巊偭偰偄傑偡丅
偺幃偺旝暘偼崌惉娭悢旝暘傪巊偭偰偄傑偡丅
椺偊偽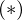 偺戞俁崁偼師偺傛偆偵旝暘傪峴偭偰偄傑偡丅
偺戞俁崁偼師偺傛偆偵旝暘傪峴偭偰偄傑偡丅
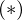 偺幃傪
偺幃傪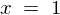 偲偍偔偲丄傑偢丄
偲偍偔偲丄傑偢丄
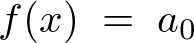
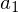 傪媮傔傞偨傔偵
傪媮傔傞偨傔偵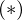 偺幃傪x偱旝暘偟丄侾傪戙擖偡傞偲丄
偺幃傪x偱旝暘偟丄侾傪戙擖偡傞偲丄
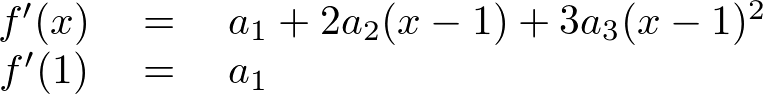
偪側傒偵
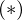 偺幃偺旝暘偼崌惉娭悢旝暘傪巊偭偰偄傑偡丅
偺幃偺旝暘偼崌惉娭悢旝暘傪巊偭偰偄傑偡丅
椺偊偽
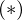 偺戞俁崁偼師偺傛偆偵旝暘傪峴偭偰偄傑偡丅
偺戞俁崁偼師偺傛偆偵旝暘傪峴偭偰偄傑偡丅
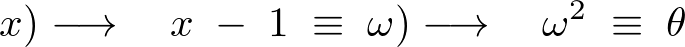
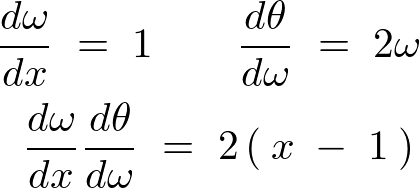
偝傜偵旝暘偟偰摨偠傛偆偵侾傪戙擖偡傟偽丄
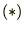 幃偼師偺傛偆偵昞尰偱偒傑偡丅
幃偼師偺傛偆偵昞尰偱偒傑偡丅
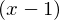 偵偮偄偰偺懡崁幃揥奐傪偟偰偒傑偟偨偑偦傟埲奜偺
偵偮偄偰偺懡崁幃揥奐傪偟偰偒傑偟偨偑偦傟埲奜偺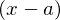 偵偮偄偰傕傑偨摨條偵側傝傑偡丅
偵偮偄偰傕傑偨摨條偵側傝傑偡丅
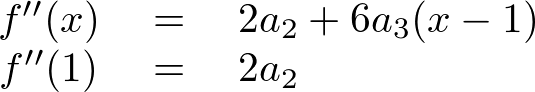
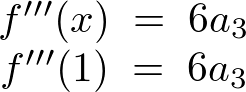
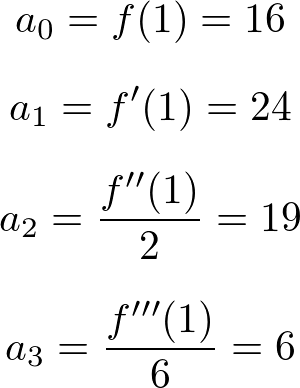
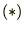 幃偼師偺傛偆偵昞尰偱偒傑偡丅
幃偼師偺傛偆偵昞尰偱偒傑偡丅
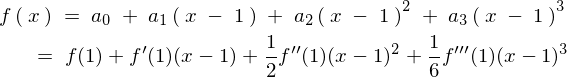
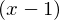 偵偮偄偰偺懡崁幃揥奐傪偟偰偒傑偟偨偑偦傟埲奜偺
偵偮偄偰偺懡崁幃揥奐傪偟偰偒傑偟偨偑偦傟埲奜偺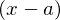 偵偮偄偰傕傑偨摨條偵側傝傑偡丅
偵偮偄偰傕傑偨摨條偵側傝傑偡丅
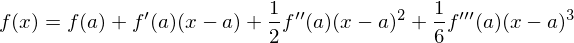
忋婰偺幃偼俁師偺懡崁幃側傜偽惉棫偡傞幃偱偁傝丄
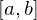 傪娷傓奐嬫娫偱
傪娷傓奐嬫娫偱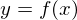 偑旝暘壜擻側偲偒師偺傛偆側偙偲偑尵偊傑偡丅
偑旝暘壜擻側偲偒師偺傛偆側偙偲偑尵偊傑偡丅
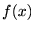 幃偺
幃偺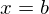 偱偺抣傪
偱偺抣傪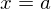 傑傢傝偱揥奐偡傞偲偄偭偨傝偟傑偡丅
傑傢傝偱揥奐偡傞偲偄偭偨傝偟傑偡丅
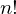 偲偄偆偺偼丄N偺僇僀僕儑僂偲傛傃丄埲壓偺傛偆偵掕媊偝傟偰偄傞傕偺偱偡丅
偲偄偆偺偼丄N偺僇僀僕儑僂偲傛傃丄埲壓偺傛偆偵掕媊偝傟偰偄傞傕偺偱偡丅
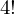 偩偭偨応崌丄
偩偭偨応崌丄
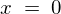 揰夞傝偵偍偗傞僥僀儔乕媺悢偑偁傝傑偡丅偙傟偼堦斒揑偵儅僋儘乕儕儞揥奐側偳偲屇偽傟偰偄傞傛偆偱偡丅
揰夞傝偵偍偗傞僥僀儔乕媺悢偑偁傝傑偡丅偙傟偼堦斒揑偵儅僋儘乕儕儞揥奐側偳偲屇偽傟偰偄傞傛偆偱偡丅
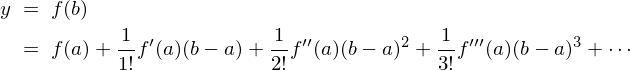
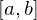 傪娷傓奐嬫娫偱
傪娷傓奐嬫娫偱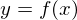 偑旝暘壜擻側偲偒師偺傛偆側偙偲偑尵偊傑偡丅
偑旝暘壜擻側偲偒師偺傛偆側偙偲偑尵偊傑偡丅
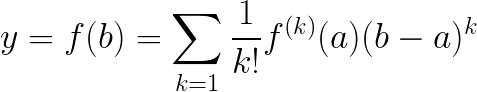
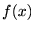 幃偺
幃偺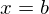 偱偺抣傪
偱偺抣傪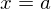 傑傢傝偱揥奐偡傞偲偄偭偨傝偟傑偡丅
傑傢傝偱揥奐偡傞偲偄偭偨傝偟傑偡丅
偪側傒偵暘曣偵偁傞
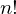 偲偄偆偺偼丄N偺僇僀僕儑僂偲傛傃丄埲壓偺傛偆偵掕媊偝傟偰偄傞傕偺偱偡丅
偲偄偆偺偼丄N偺僇僀僕儑僂偲傛傃丄埲壓偺傛偆偵掕媊偝傟偰偄傞傕偺偱偡丅
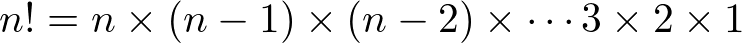
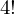 偩偭偨応崌丄
偩偭偨応崌丄
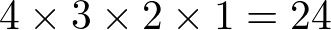
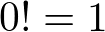
忋婰偺傗傝曽偵庤傪偔傢偊偨傕偺偱
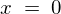 揰夞傝偵偍偗傞僥僀儔乕媺悢偑偁傝傑偡丅偙傟偼堦斒揑偵儅僋儘乕儕儞揥奐側偳偲屇偽傟偰偄傞傛偆偱偡丅
揰夞傝偵偍偗傞僥僀儔乕媺悢偑偁傝傑偡丅偙傟偼堦斒揑偵儅僋儘乕儕儞揥奐側偳偲屇偽傟偰偄傞傛偆偱偡丅
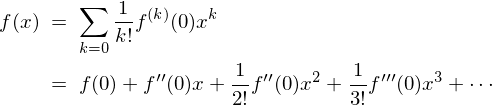
椺戣
師偵帵偡娭悢偺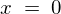 廃傝偱偺僥僀儔乕揥奐乮儅僋儘乕儕儞揥奐乯丅
廃傝偱偺僥僀儔乕揥奐乮儅僋儘乕儕儞揥奐乯丅
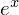 偼
偼 偱偄偔傜旝暘偟偰偄偭偰傕摨偠寢壥偑弌偰偔傞偺偱侽揰傑傢傝偺僥僀儔乕揥奐丄
偱偄偔傜旝暘偟偰偄偭偰傕摨偠寢壥偑弌偰偔傞偺偱侽揰傑傢傝偺僥僀儔乕揥奐丄
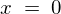 廃傝偱偺僥僀儔乕揥奐乮儅僋儘乕儕儞揥奐乯丅
廃傝偱偺僥僀儔乕揥奐乮儅僋儘乕儕儞揥奐乯丅

(1)
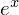 偼
偼 偱偄偔傜旝暘偟偰偄偭偰傕摨偠寢壥偑弌偰偔傞偺偱侽揰傑傢傝偺僥僀儔乕揥奐丄
偱偄偔傜旝暘偟偰偄偭偰傕摨偠寢壥偑弌偰偔傞偺偱侽揰傑傢傝偺僥僀儔乕揥奐丄
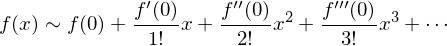
偵摉偰偼傔傟偽丄埲壓偺傛偆偵側傞丅
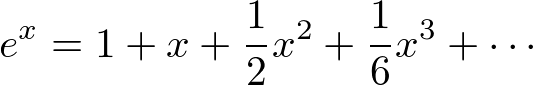
(2)
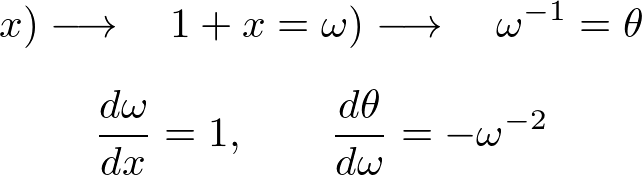
側偳偲傗偭偰俁奒旝暘傑偱傗偭偰偄偔偲丄
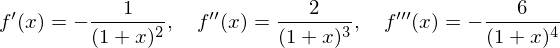
偺傛偆偵側傝傑偡丅偙傟傪戙擖偟偰偄偗偽丄
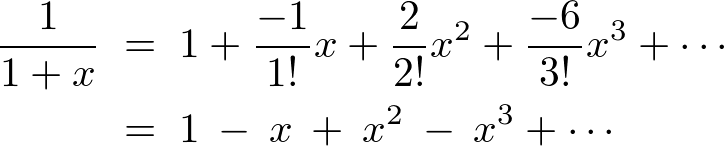
愝栤偺椺
栤戣偺拞偵偼僥僀儔乕揥奐偣傛丄偲柧妋偵昞尰偡傞偙偲側偔師偺傛偆側姶偠偱弌戣偝傟傞偙偲傕偁傝傑偡丅
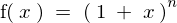 偲偄偭偨幃偑偁偭偨応崌丄偙偺娭悢
偲偄偭偨幃偑偁偭偨応崌丄偙偺娭悢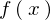 傪戞3崁傑偱偺傋偒媺悢揥奐偟偰昞帵偣傛丄側傫偰偄偆愝栤偑偁偭偨応崌偼偨偄偰偄偼師偺傛偆偵儅僋儘乕儕儞揥奐偟偰栤戣傪夝偄偰偄偒傑偡丅
傪戞3崁傑偱偺傋偒媺悢揥奐偟偰昞帵偣傛丄側傫偰偄偆愝栤偑偁偭偨応崌偼偨偄偰偄偼師偺傛偆偵儅僋儘乕儕儞揥奐偟偰栤戣傪夝偄偰偄偒傑偡丅
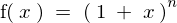 偲偄偭偨幃偑偁偭偨応崌丄偙偺娭悢
偲偄偭偨幃偑偁偭偨応崌丄偙偺娭悢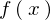 傪戞3崁傑偱偺傋偒媺悢揥奐偟偰昞帵偣傛丄側傫偰偄偆愝栤偑偁偭偨応崌偼偨偄偰偄偼師偺傛偆偵儅僋儘乕儕儞揥奐偟偰栤戣傪夝偄偰偄偒傑偡丅
傪戞3崁傑偱偺傋偒媺悢揥奐偟偰昞帵偣傛丄側傫偰偄偆愝栤偑偁偭偨応崌偼偨偄偰偄偼師偺傛偆偵儅僋儘乕儕儞揥奐偟偰栤戣傪夝偄偰偄偒傑偡丅
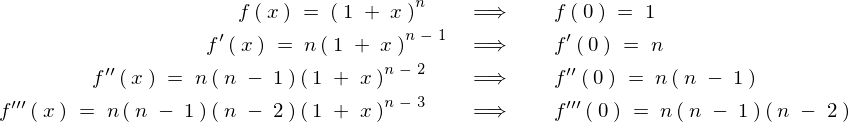
傛偭偰夝摎偺椺偲偟偰偼埲壓偺傛偆偵側傞丅
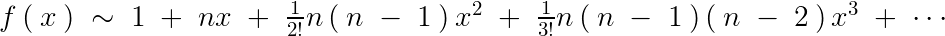
曗堚
偡傋偰偺媺悢偑僥僀儔乕揥奐偱偆傑偔偄偔偲偼尷傝傑偣傫丅
椺偊偽師偺傛偆側幃傪媺悢揥奐偡傞応崌偼僥僀儔乕揥奐傪偡傞偲偛偪傖偛偪傖偟偨幃偑弌偰偔傞偺偱暿偺曽朄傪巊偄傑偡丅
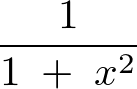
傑偢丄
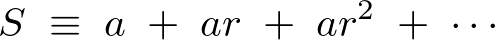
偺傛偆側媺悢傪峫偊偰丄偦傟偵偝傜偵掕悢崁偺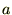 傪椉曈偵壛偊偨傕偺傪梡偄偰師偺傛偆側幃傪摫偒傑偡丅
傪椉曈偵壛偊偨傕偺傪梡偄偰師偺傛偆側幃傪摫偒傑偡丅
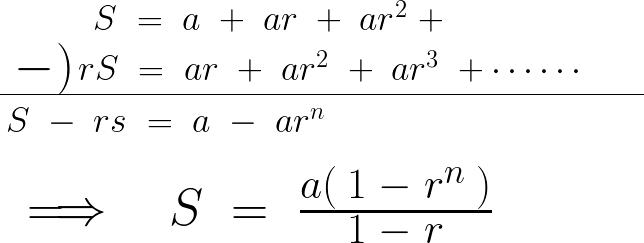
偙偙偱値傪亣偲偟偰壖掕偡傟偽丄
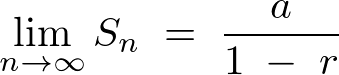
偵摉偰偼傔偰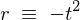 偲偍偄偰忋幃偵摉偰偼傔偰偄偗偽丄
偲偍偄偰忋幃偵摉偰偼傔偰偄偗偽丄
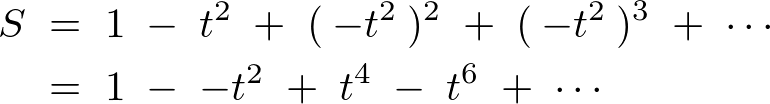
偙偙偱偙偺幃偺椉曈傪侽偐傜侾偺掕愊暘傪幚峴偡傞丅
傑偢塃曈偼丄
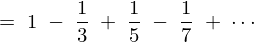
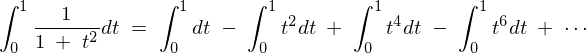
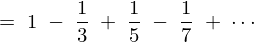
堦曽丄嵍曈偺愊暘偵娭偟偰丄僥僀儔乕揥奐偺旝暘偼丄
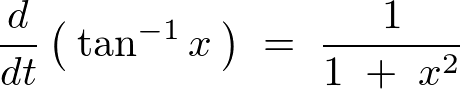
偱偁偭偨偺偱侽偐傜侾傑偱偺掕愊暘傪峴偆偲丄
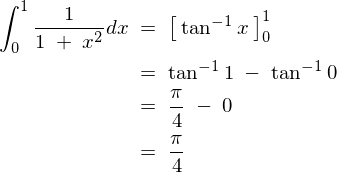
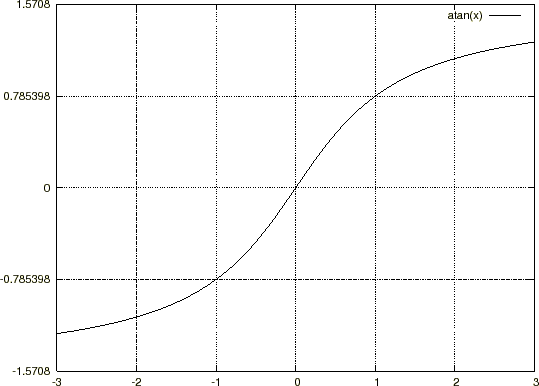
偙偙偱嵍恾傾乕僋僞儞僕僃儞僩偺僌儔僼傛傝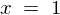 偺偲偙傠偱岎傢傞
偺偲偙傠偱岎傢傞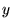 幉偺抣偺0.785乧偲尵偆悢帤偼3.14乧傪係偱妱偭偨悢丄偡側傢偪
幉偺抣偺0.785乧偲尵偆悢帤偼3.14乧傪係偱妱偭偨悢丄偡側傢偪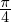 偵側傝傑偡丅
偵側傝傑偡丅
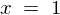 偺偲偙傠偱岎傢傞
偺偲偙傠偱岎傢傞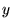 幉偺抣偺0.785乧偲尵偆悢帤偼3.14乧傪係偱妱偭偨悢丄偡側傢偪
幉偺抣偺0.785乧偲尵偆悢帤偼3.14乧傪係偱妱偭偨悢丄偡側傢偪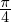 偵側傝傑偡丅
偵側傝傑偡丅
偲側傞偺偱師偺傛偆側娭學幃偑摫偐傟傑偡丅
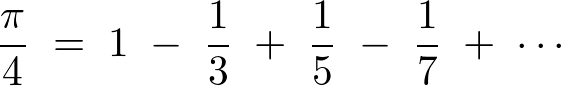
偙偺幃偼寢峔桳柤側悢幃傜偟偔丄悢妛偺撉傒暔揑側僥僉僗僩側傫偐偱偼偨傑偵徯夘偝傟傞偙偲傕偁傞傛偆偱偡丅
堦斒揑偵偼僌儗僑儕乕偺岞幃丄傑偨偼儔僀僾僯僢僣偺岞幃側偳偲偄傢傟偰偄傞傜偟偄偱偡丅























