お知らせ
当Webサイトはサイト作成システムの深刻な欠陥により現在リンクの変更を行っております。管理人が多忙のためリダイレクトサイトは作成せず、直接リンク変更を行う予定です。何卒ご了承ください。時期は未定になります。
既存のページはなるべく残すようにしますが直で変更しますのでブックマークなどしている方は、ご面倒になるかと思いますがこのドメインhttps://mathematical.jp/mathematical/ から目的のページに行くようにお願い申し上げます。
フリードマン・ルメートル宇宙の解釈
宇宙論パラメーターの導入
宇宙論を考察する前の準備としていろいろなパラメーターをリストアップします。
ハッブルパラメーター
ドットaは時間微分として、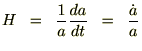
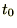 のハッブルパラメーターをハッブル定数として、
のハッブルパラメーターをハッブル定数として、
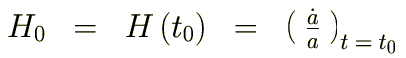
曲率パラメーター
kで表して次のように定義します。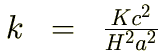
現在値として ⇒ 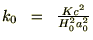
宇宙項パラメーター
λで表して次のように置きます。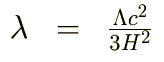
現在値として ⇒ 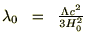
密度パラメーター
つぎの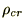 を臨界密度とします。
を臨界密度とします。
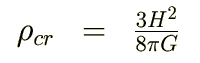
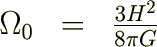
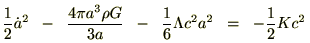
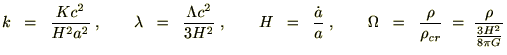

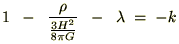
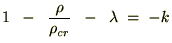
これらの結果により次の式が導かれます。
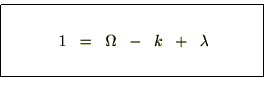
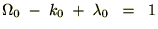
フリードマンルメートル宇宙モデルE=Vのとき
とりあえず細かい過程は端折って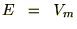 であるならば、先ほどの曲率パラメーターkは他のパラメーターを使って次のように表せるとします。
であるならば、先ほどの曲率パラメーターkは他のパラメーターを使って次のように表せるとします。
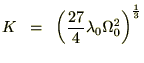
 というのを思い出せば、
というのを思い出せば、
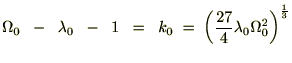
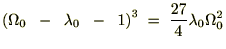
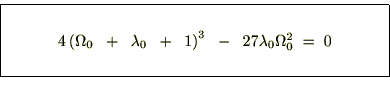
宇宙理論応用3次方程式その①関連ページ
- 宇宙論応用3次方程式②
- 3次方程式の解法と、それを使用したフリードマンルメートル宇宙モデル(E=V)への応用について考察します。2次方程式は高校の時に習いますが3次方程式を習うことはほとんどないと思います。そのためか難易度が高いためと思わがちですがそんなことはありません。特に小難しい数学知識がなくても理解できることでしょう。

















