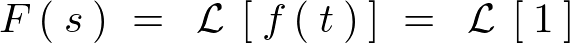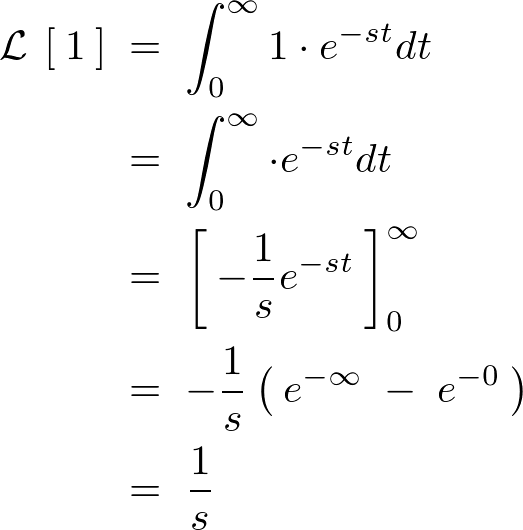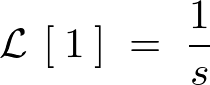���ԂɊւ������
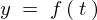
�Ƃ��Ă��̊����A
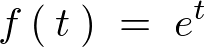
�ƒu�����Ƃ��܂��B
�����
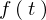
�ɑ���
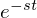
�����������
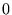
����v���X�̖�����
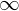
�͈̔͂ɂ����Đϕ����A���̐ϕ��ɂ����
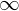
�Ƃ͈Ⴄ���ɕϊ����邱�Ƃ����v���X�ϊ�����Ƃ����܂��B
�t�[���G�ϊ��R���e���c�ł��������悤�Ɏ���T�̐��E�̂ŕ\������Ă������f���̂��̐��E�̊��ɒu�������邱�Ƃɂ��A�ʏ�ł͊ȒP�ɂ͉����Ȃ��悤�ȕ��G�Ȕ��������������̃��v���X�ϊ����s�����Ƃɂ���Č��ʂ��i�v�Z���ȑf���j���悭����Ƃ��������_������܂��B
���ۂ̌v�Z
�����ŏ�L�����̏搔���������̂悤�ɂ����Ēu���ϕ����Ă����܂��B
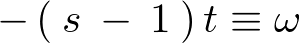
�ƒu�����Ă����

�Ŕ�������ƁA
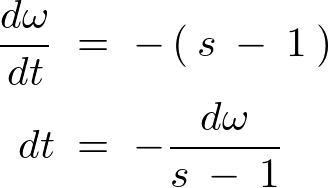
�Ƃ������ϐ�
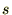
�̊��ɕϊ�����܂��B
���̂悤�ȕϊ������̂��߂ɍs���̂������Ƃ���������������㐔�I�Ȍv�Z�ɂ���ĉ������Ƃ��\�ɂȂ�Ƃ��������_������܂��B
���Ԋ����萔�̏ꍇ�̃��v���X�ϊ�
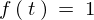 �̏ꍇ�̃��v���X�ϊ�
�̏ꍇ�̃��v���X�ϊ�
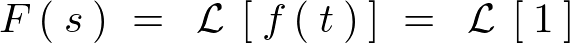
���A
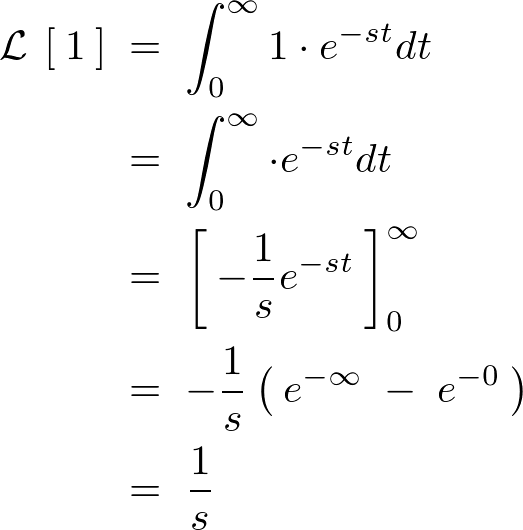
�����莞�Ԋ����萔�̏ꍇ�̌��ʂ͎��̂悤�Ȏ��ɕϊ�����܂��B


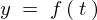 �Ƃ��Ă��̊����A
�Ƃ��Ă��̊����A
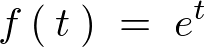
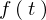 �ɑ���
�ɑ���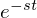 �������Ă����
�������Ă����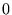 ����v���X�̖�����
����v���X�̖�����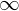 �͈̔͂ɂ����Đϕ����A���̐ϕ��ɂ����
�͈̔͂ɂ����Đϕ����A���̐ϕ��ɂ����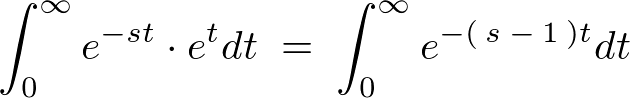
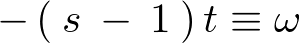
 �Ŕ�������ƁA
�Ŕ�������ƁA
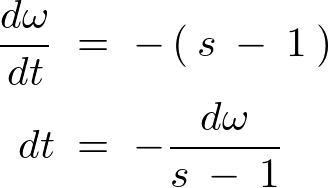
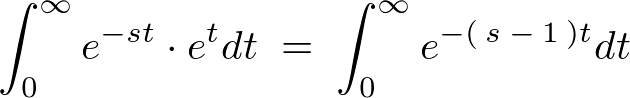
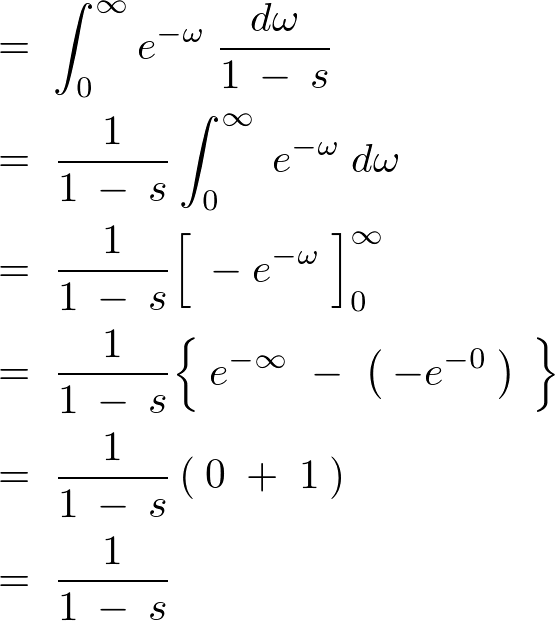
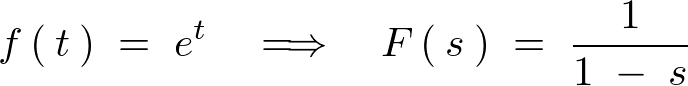
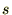 �̊��ɕϊ�����܂��B
�̊��ɕϊ�����܂��B
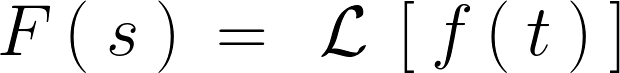
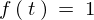 �̏ꍇ�̃��v���X�ϊ�
�̏ꍇ�̃��v���X�ϊ�