�y��O�́z���x�N�g���̊T�O
�x�N�g����͂Ƃ́A��ԃx�N�g����p�������̕������w�Ƃ������镪��ł���A����̕����w�ɂ����邳�܂��܂ȕ���ɂ����Ċ��p����Ă���ɂ߂ďd�v�ȗ��_�I�T�O�ł��B
���ɓd���C�w�𗝉����邽�߂ɂ͌����Ĕ����Ă͒ʂ�Ȃ����ɏd�v�ȕ���Ƃ����܂��B
�������Ȃ����w�ŏK���x�N�g����͂Ƃ����̂͋`�����瓙�ŏK���g�x�N�g���h�Ƃ͂����ԈقȂ�`�Ԃ�v���Ă���̂ŁA���w�҂ɂƂ��ĂƂ���������������镔�������Ȃ��炸����܂��B
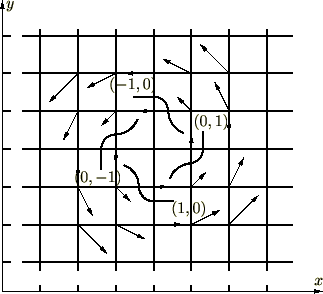
���T�C�g�ł͂��̕������Ȃ�ׂ��Ȃ��A�킩��Â炢�\�L������͂Ȃ�ׂ������Ȃ��琔�w�̋��ȕ��ł������ł��邱�Ƃ�ړI�Ƃ��A����ɂ̓r�M�i�[�ɂƂ��ē���݂₷���悤�ɏK�n�����A�Ɗw�ł��̕���ɂ����鏉���I����{�I�ȓ��e���y�I���₩�ɗ������K�������邽�߂̃T�|�[�g����̖ړI�Ƃ��Ă��܂��B
�x�N�g���Ɋւ��Ă̂����炢
�g�x�N�g���h�Ƃ����T�O�͍��Z���w�ŏK�����Ƃ���A�g�����h�ƁA���́g�傫���h���������ʂł��B����x�N�g��
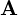 �ƃx�N�g��
�ƃx�N�g��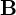 ���������Ƃ��܂��B����̍������l����Ή��}
���������Ƃ��܂��B����̍������l����Ή��}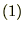 ���A�x�N�g��
���A�x�N�g��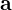 �̎n�_����
�̎n�_����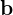 �̏I�_�����x�N�g��
�̏I�_�����x�N�g��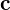 �̑傫���ł��B
�̑傫���ł��B
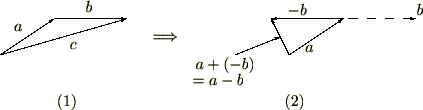
����ɏ�}
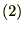 ���A�x�N�g���̍��͘a�ŕ\�����Ƃ��o���܂��B
���A�x�N�g���̍��͘a�ŕ\�����Ƃ��o���܂��B
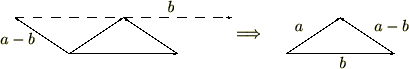
����x�N�g��
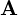 �ɂ�����
�ɂ�����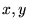 �����̐��������ꂼ��
�����̐��������ꂼ��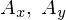 �Ə����A����
�Ə����A����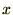 ���A
���A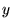 ���̐��̕����ɑΉ������傫����
���̐��̕����ɑΉ������傫����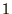 �̃x�N�g���� �P�ʃx�N�g��
�̃x�N�g���� �P�ʃx�N�g��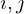 �Ƃ���ƁA�x�N�g��
�Ƃ���ƁA�x�N�g��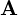 �́A
�́A
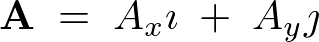
����ɁA���̃x�N�g��
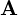 �̑傫����
�̑傫����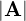 �Ƃ���A
�Ƃ���A

��x�N�g��
����x�N�g��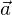 ������Ƃ��A���̃x�N�g���Ƒ傫���������ł���Ȃ�������������̃x�N�g�����������Ƃ��܂��B
������Ƃ��A���̃x�N�g���Ƒ傫���������ł���Ȃ�������������̃x�N�g�����������Ƃ��܂��B
�����
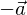 �Ƃ���Ȃ�A���̉��@���l�����
�Ƃ���Ȃ�A���̉��@���l�����
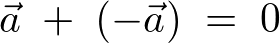
�n�_�ƏI�_����v���Ă��邽�߂ɂ��̂悤�ɕ\���ł��܂��B
����͌������������Ƃ͂����܂���̂ŁA�����傫����
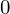 �̔C�ӂ̌��������x�N�g���ƍl��
�̔C�ӂ̌��������x�N�g���ƍl��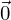 �ƕ\���܂��傤�B
�ƕ\���܂��傤�B

���ρi�h�b�g�v���_�N�g�j
2�̃x�N�g��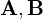 ���������Ƃ��A����̍��p��
���������Ƃ��A����̍��p��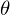 �������Ƃ��܂��B
�������Ƃ��܂��B
���̂Ƃ��A
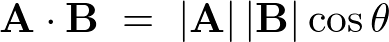
�ɂ����鍶�ӂ̕�������ρA�܂��̓h�b�g�v���_�N�g�ȂǂƂ������肵�܂��B
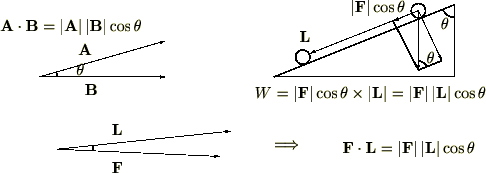
�͂̌����ƕω��x�N�g���̕��������������A�R�T�C����
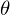 ��
��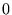 �Ƃ���悭�A���̏ꍇ�ɂ́A
�Ƃ���悭�A���̏ꍇ�ɂ́A
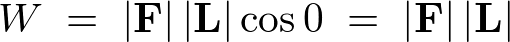
�ƂȂ�܂��B
���ɂR�����̏ꍇ�ɂ����Ă̒P�ʃx�N�^�[�̓��ς��l���Ă݂܂��傤�B
�����P�ʃx�N�g���̓��ς́A
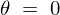 ���A
���A
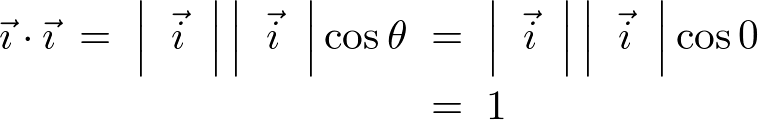
���l�ɂ��āA
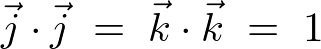
�قȂ�P�ʃx�N�g���̓��ς́A
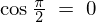 ���A
���A
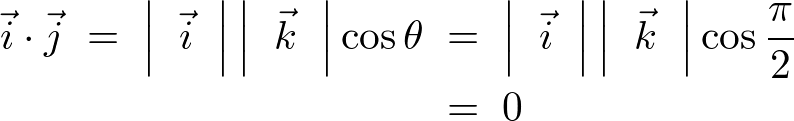
���l�ɂ���
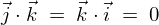 �ƂȂ�܂��B
�ƂȂ�܂��B
�O�ρi�N���X�v���_�N�g�j
�}�̂悤�Ȑ�������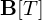 �̒��ɁA�d��
�̒��ɁA�d��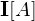 ������Ă��钷��
������Ă��钷��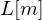 �̓�����u���ƁA���̓����ɂ͉��}�E���Ɏ����悤�ȕ����ɗ́i�d���́j
�̓�����u���ƁA���̓����ɂ͉��}�E���Ɏ����悤�ȕ����ɗ́i�d���́j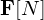 �������܂��B
�������܂��B
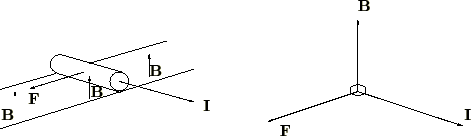
��}�ɂ����Ă͎���Ɠd���̕����͐����ɂȂ��Ă��܂��B
���̂Ƃ��̓d���͂̑傫���́A
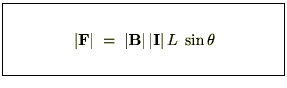

�����́g�ρh���A
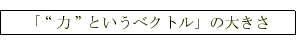
�ł́A���x�͎���̌����Ɠd���̌����������ł͂Ȃ��ꍇ�͂ǂ��Ȃ�ł��傤���H
���̐}�̂悤��
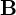 ���p�x
���p�x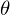 �����ς����Ƃ��܂��B
�����ς����Ƃ��܂��B
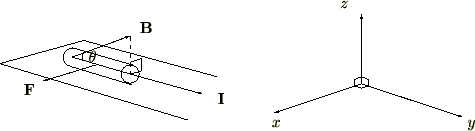
���̂悤�ȂƂ��A�͂̌����͓����ł���
 �̑傫�������̂悤�ɕω����܂��B
�̑傫�������̂悤�ɕω����܂��B
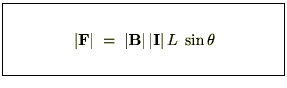
�C�ӂ̌����̎���
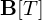 ���œd��
���œd��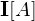 �̗���钷��
�̗���钷��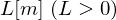 �̓����ɓ�����
�̓����ɓ�����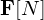 �́A�܂Ƃ߂�Ǝ��̂悤�ɂȂ�܂��B
�́A�܂Ƃ߂�Ǝ��̂悤�ɂȂ�܂��B
| �傫�� | 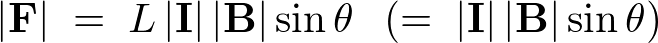 |
|---|---|
| ���� | ����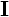 �� ��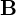 �ɐ����ŁA �ɐ����ŁA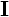 ���� ����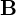 �։��E�˂��̐i�ޕ��� �։��E�˂��̐i�ޕ��� |
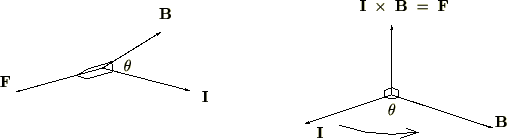
�E�˂��̐i�ތ����Ƃ��Ă���̂ŁA���̂��Ƃɂ��A
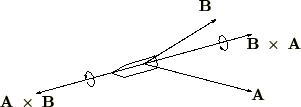
�ƂȂ�܂��B
�܂�A
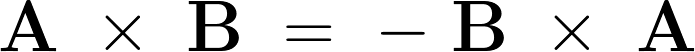
�g�O�ς͔���ł���h�Ƃ������Ƃ������܂��B
���̃T�C�g�̎�|
- �{���Ώێ҂͂����ɑ�w���N�x�̕����w�Ȃ̊w����Ώ̂Ƃ��Ă��܂����Љ�l�⍂�Z���Ȃǂ̈�ʂ̕��ɑ��Ă��A�����ϕ��̊ȒP�Ȓm����������܂薳���Ȃ��ǂݐi�߂邱�Ƃ��o���邩�Ǝv���܂��B
���e�����ϋy�ъO�ςȂǂ̐��w�I��ʉ�����A�x�N�g���̔����ϕ��A����ɂ��X�J���[��E�x�N�g����Ȃǂ̐��w�I��舵���A�������x�N�g���ꔭ�U�i�_�C�o�[�W�F���X�j�y���x�N�g�����]�i���[�e�[�V�����j�Ȃǂ̊T�O��v�Z�@�ȂǂƂȂ��Ă��܂��B�y�[�W�̐i�ߕ��̓y�[�W���ɂ���
 �{�^���������Ă����Ώ��ʂ�Ƀy�[�W���i��ł����d�g�݂ɂȂ��Ă��܂��B�Ȃ��ړI�̃y�[�W���������ꍇ�͂�������T�C�g�}�b�v��肨�i�݂��������B
�{�^���������Ă����Ώ��ʂ�Ƀy�[�W���i��ł����d�g�݂ɂȂ��Ă��܂��B�Ȃ��ړI�̃y�[�W���������ꍇ�͂�������T�C�g�}�b�v��肨�i�݂��������B - �Ȃ��A�O�ϋy�у��[�e�[�V�����i�q�n�s�v�Z�j�ɂ�����s��v�Z�̓T���X�@�ɂ��Ȃ��w�s�W�J�@�x�ƌĂ��v�Z�@����Ă���܂��B ���̌v�Z�@�͎��ɒP�������ɗ��v�Z�@�ł��̂ł��܂����l�����Ɍy���C�����Ŋw�K���Ă����Ă��������B�܂��A�x�N�g���O�ς�[�e�[�V�����i�q�n�s�v�Z�j�Ȃǂ̂R�s�R��̌v�Z�݂̂Ȃ炸�A����ȏ�̍s��Ȃǂ̌v�Z������ʎq�͊w�Ȃǂ̕���ŕK�v�ɂȂ��Ă��܂��̂ŕ������u�����ł���Ȃ���̌v�Z�@�͊o���Ă����đ��͂Ȃ����Ƃł��傤�B
- ���̈���p�y�[�W�ɑ�R�͈ȍ~�ɂ����Ẵx�N�g�����z����}���邽�߂̕\������Ă���܂��B�O���[�X�P�[������Ȃǂ��w�肵�ăv�����g�A�E�g���Ďg���Ă��������B
�������N�t���[�ł��B����ȃT�C�g�ł悩�����珟��Ƀ����N���Ă��������i�O�ցO�j�������ް
���̃`���v�^�[�ł̓x�N�g���ɂ�����㐔�I�ȍl�����A����ɂ͂����W�������X�J���[�O�d�ρA�x�N�g���O�d�ςɂ��čl�@���Ă����܂��B
�y�[�W�̐i�ߕ��͉��� �{�^���������Ă����Ώ��ʂ�Ƀy�[�W���i��ł����d�g�݂ɂȂ��Ă��܂��B
�{�^���������Ă����Ώ��ʂ�Ƀy�[�W���i��ł����d�g�݂ɂȂ��Ă��܂��B