�p�N��u���O�o�ŋF��R���e���c�X�V��3�e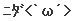
�P�������Ɍ����ƁA���̃G���g���[���m�����x���ƕϐ��ϊ��R���e���c�̑����ł͂��邪�悭�킩�銵�����[�����g�̍X�V�R���e���c�����˂Ă���B
�f�B���N�g���\���Ƃ��Ă��������v�w�̔z���ɂ���T�u�J�e�S���[���m���̐����̒��ňȉ��̂悤�ɔz�u���Ă���G���g���[�i�R���e���c�j�ɂȂ�B
�������v�w�i�J�e�S���j
���T�C�g�͌��X�͕������̃T�C�g�ł��蕨����U�̐l���炩�炷��Δ����ϕ��A��͗͊w�ȂǂŎg������̂��Ȃ��������v�w�̑��ϗʉ�͂ɁH�ƖʐH�炤�l�����邾�낤���A���̃��R�r�A���Ƃ����̂͑��ϗʉ�͂ɂ����Ă悭�o�ꂵ�A���������\�d�v�Ȗ������͂����Ă���B
����Ɋւ��Ă͏���ǂ��ĉ�����Ă������Ǝv���B
���Ȃ݂ɏ����f�[�^�G���W�j�A�Ƃ������V�X�e���G���W�j�A��ڎw���Ă���l�Ȃǂ͑��ϗʉ�͂̒m����K�v�Ƃ����ꍇ������Ǝv�����A����ɑΉ������ۂɂ������������̒m��������̂��ɖ𗧂��e�ɂȂ��Ă���Ǝv���B
�悭�킩�銵�����[�����g�̃��R�r�A���R���e���c�̒lj��h���R��
���̃h���C�����ł̐��w�����֘A�̃R���e���c�͊�{�I�Ƀh���t�g�R���e���c�ł���A����{�T�C�g�̂ق��ֈڂ��ۂ̍��NjL���݂����Ȃ��̂�u���ꍇ������B
����̃R���e���c�͂���ɂ�����B
�O�X���猾���Ă���悤�ɃT�e���C�g�T�C�g���悭�킩�銵�����[�����g��M���ɂ��āA����ȊO�ɂ��T���ł��킩����`�㐔���悭�킩��x�N�g������Ƃ��������̃h���C�����̃R���e���c���p�����ɂȂ��Ă���A���̑�Ƃ��ẴR���e���c�X�V�y�т��̊g�[�̈�ɂȂ�B
�X�V�����Ă��Ȃ����R
���Ƃ��Ɩ{�E���Z�����Ƃ����̂��{���Ƃ��Ă��邪���܂ŃR���e���c���g�[���Ă��Ȃ������͓̂�����_��l�����Ȃǂ͏�����Web�T�C�g�ւ̓�����Ƃ������Ԍ����L�����Ă������������Ƃ����̂�����B
�Ⴆ�悭�킩�銵�����[�����g�Ɋւ���h���m���Ƃ��āg�������[�����g�e���\���h�ȂǂƂ��������̂����邪�A���܂萔�w�Ɋ���e����łȂ��l�̏ꍇ���̒P��i�e���\���j���o�Ă������_�ł����́g�q����i�T�C�g�ɖK��Ă������ɗ����j�h�ɂȂ�\��������B
�������������Ƃ�����邽�߂Ɏ����^�c���鐔�w�����w�R���e���c�͂Ȃ�ׂ�������e������Ȍ����������x���ŗ����ł��邱�Ƃ�ڕW�Ƃ����T�C�g�쐬��S�����Ă���Ƃ������������̈���ɂȂ��Ă���B
�܂��{�Ƃ��Ă͓���Ƃ��Ă̐��w��g�ɕt���Ă��炢�Ȃ��炻�̑��̃R���e���c�A�Ƃ�킯�����Ɋւ���R���e���c�ɂ������������Ă��炤���߂̕z�ƂȂ�ׂ�����Ă���A���̑Ώۂ͈�ʎЉ�l���͂��߂Ƃ��A���w�E���Z���Ƃ������܂��P�O��̊w������A����ɗ~�������Ώ��w���ł��Ӗ����x�Ȃ痝���ł��ċ����������Č��Ă��炦����̂�ڕW�Ƃ����R���e���c�쐬�����ɂ����Ă���B
�������Ȃ�������̃R���e���c���p�̏��ӂ݂�T�C�g�̓��e����ɍX�V���A������x�̐�含���������Ȃ���R���e���c�̗ʂ𑝂₵�Ă������Ƃ���Ԃ̑�ɂȂ�Ƃ����̂�����Ƃ��Ă���A������R���e���c�̊g�[�����Ȃ���{���̃T�C�g�쐬�̕������������ύX���Ă����Ȃ���Ȃ�Ȃ��������Ȃƍl���Ă���B
�悭�킩�銵�����[�����g�A�p�[�}�����N�X�V��3�e
�Ƃ������ƂőO��A��1�e�A�����đ�2�e�Ƃ��ĉ~���̊������[�����g����舵�������A���x�͑�3�e�Ƃ��ă��R�r�A�������グ�邱�Ƃɂ����B
�薼�Ƃ��Ắu�ϐ��ϊ��ƃ��R�r�A���v�ł��邪�A����͂��Ƃ��Ɛ������v�w�̒��̃R���e���c�A�u���ϗʊm���x�N�g���̌v�Z�v�@���@�u�m�����x���ƕϐ��ϊ��v�A�Ƃ��������e�̑����Ƃ��čl���Ă����R���e���c�ɂȂ�B
���̃��R�r�A���Ƃ������̂Ɋւ��Ắu�悭�킩�銵�����[�����g�v�̒��̃T�u�J�e�S���R���e���c�ɂ��u���R�r�A���v�Ƃ����̂�����A����ɕt���R���e���c�Ƃ��Ď��グ��\��ɂȂ��Ă���B
�K����苳����ق�������Ƃ����T�^�ᄪ���R�r�A��
��ʓI�ɂƂ������܂��Ȃ�ł������Ȃ̂��������ŗ�������������l�ɋ����邱�Ƃ̂ق�������Ƃ����̂͂悭�����邪�A�����w�ɂ����銵�����[�����g�̎��Ӓm���Ƃ��Ă킩�肸�炢�A�܂��͑��҂ɋ����ė������Ă��炤�̂���⍢��Ȃ��̂Ƃ��Ă͐�قǏグ���������[�����g�e���\���ȊO�̂��̂Ƃ��č�����グ�邱�̃��R�r�A���Ƃ������̂ɂȂ�B
����Ƃ��Ďg�������Ȃ�ΐ��`�㐔�ɂ�����s�̌v�Z���ł������œ��ɖ�肪�Ȃ����̂ɂȂ邪�A���W�ϊ�������ۂ̎ʑ��ɂ����ĂȂ����R�r�s��Ƃ������̂��o�Ă���̂��A�Ƃ��������̍��{�I�ȍl�����Ɛ����ɂȂ��Ă���B

�͂��͂�����ł͂܂����R�r�A���ɂ�����ϐ��ϊ��Ƃ͂Ȃ�Ȃ̂�����������Ă����܂��傤�B
�������d�����邪�����܂Ńh���R���̈���o�Ȃ��̂ł��Ȃ�e���ŁA�������Ǝ��̍l�@�ɂ����e�ɂȂ��Ă���̂ł��̂ւ�͒��ӂ��ĉ{������悤�ɁB
���R�r�A���Ƃ�
���߂Đ�������Ƒ��ϗʉ�͂ɂ����ďd�v�Ȋm�����z�ő��ϗʐ��K���z�Ƃ����̂�����A������ۂɏd�v�Ȃ��̂Ƃ��ă��R�r�A���i���s�j�Ƃ����̂�����B
�ϐ��ϊ��ɂ�����d�ϕ��̌����ł͈ȉ��̂悤�ɂȂ��Ă���B
��L���̐�Βl�ň͂܂�Ă���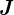 �����̃��R�r�A���ɓ�����B
�����̃��R�r�A���ɓ�����B
��ʓI�ɍ��W�n�Ƃ�����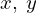 �ŗ^����ꂽ�ꍇ�ʏ�f�J���g���W�n�Ƃ��������̂��g���B
�ŗ^����ꂽ�ꍇ�ʏ�f�J���g���W�n�Ƃ��������̂��g���B
�����ł���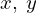 �ɑ��ĐV����
�ɑ��ĐV����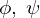 �Ƃ����������l���Ă��̕ϐ���
�Ƃ����������l���Ă��̕ϐ���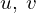 �ƒu���A���ꂪ
�ƒu���A���ꂪ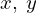 �Ƃ͉t�I�ȊW�ł���Ƃ��Ď��̂悤�Ȏ����l���邱�Ƃɂ���B
�Ƃ͉t�I�ȊW�ł���Ƃ��Ď��̂悤�Ȏ����l���邱�Ƃɂ���B
��L�̊��ɂ����� ���ʏ�̓_
���ʏ�̓_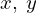 ��
�� ���ʏ��
���ʏ��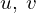 �ɑΉ�����Ƃ����}�`���l�����ꍇ�A��ʓI�ɂ�����ʑ��Ƃ����Ăѕ�������B
�ɑΉ�����Ƃ����}�`���l�����ꍇ�A��ʓI�ɂ�����ʑ��Ƃ����Ăѕ�������B
 ���ʏ�̓_
���ʏ�̓_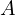 ���N�_�ɂ������̒���
���N�_�ɂ������̒���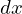 �A�c�̒�����
�A�c�̒�����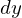 �̒����`�̔����ʐ�
�̒����`�̔����ʐ�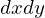 ���l���Ă��̒��_�����ꂼ��
���l���Ă��̒��_�����ꂼ��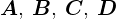 �Ƃ��āA���̂悤�Ȕ����ʐρA
�Ƃ��āA���̂悤�Ȕ����ʐρA
���̔����ʐςɂ����钷���`�̖ʐς� �ƒu�����Ƃɂ���B
�ƒu�����Ƃɂ���B
 �̃R�[�h�ꗗ�ł��B
�̃R�[�h�ꗗ�ł��B �R�[�h
�R�[�h
 �R�[�h
�R�[�h
 �R�[�h
�R�[�h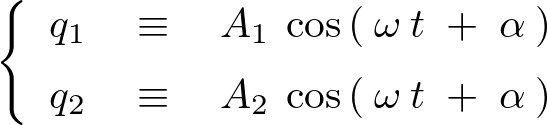
 �R�[�h
�R�[�h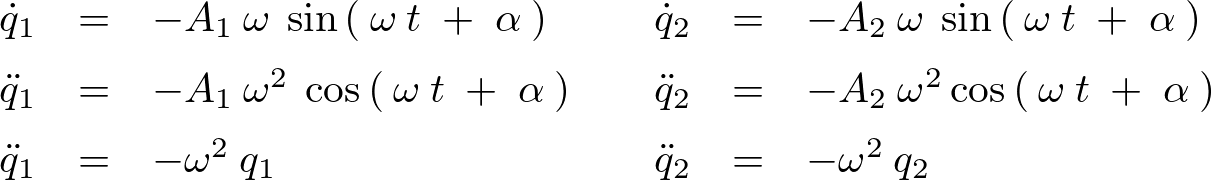


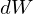 �ȊO�̋L���͑�̂̏ꍇ���͏㑤�̂ق��ɗ���悤�ɂȂ��Ă���B
�ȊO�̋L���͑�̂̏ꍇ���͏㑤�̂ق��ɗ���悤�ɂȂ��Ă���B

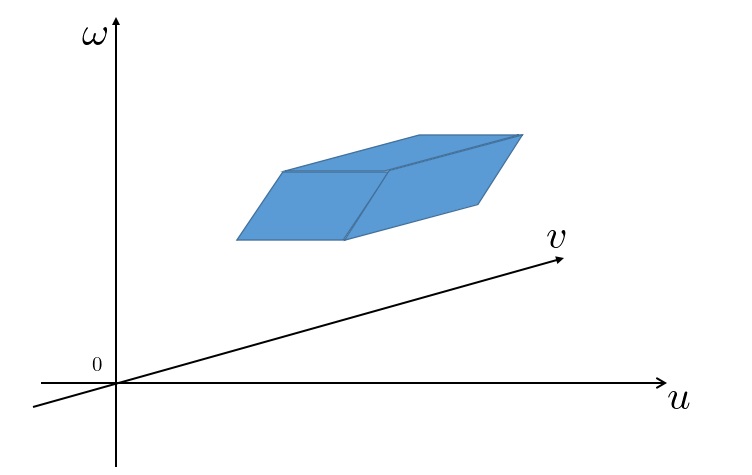
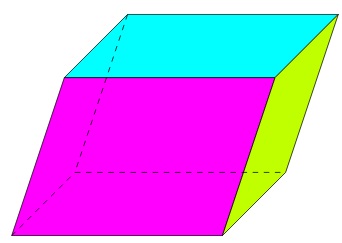
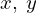 �̃J�[�e�V�������W�n����ʂ̍��W�n�̕��ʋɍ��W�nr-�Ƃւ̕ϊ����l�����ꍇ�A�����ʐ�dxdy�ɑ���r-�Ƃ̔����ʐςɑ��Ăǂ̒��x�̃X�P�[���ϊ��ʂ��X�J���[�{����Γ����̖ʐϑf���ɂȂ邩���l����Ƃ��A�܂��A���̊w�I�ȊW���ʑ��Ƃ����W���ɂ���Ď��̂悤�ȑ����W�A
�̃J�[�e�V�������W�n����ʂ̍��W�n�̕��ʋɍ��W�nr-�Ƃւ̕ϊ����l�����ꍇ�A�����ʐ�dxdy�ɑ���r-�Ƃ̔����ʐςɑ��Ăǂ̒��x�̃X�P�[���ϊ��ʂ��X�J���[�{����Γ����̖ʐϑf���ɂȂ邩���l����Ƃ��A�܂��A���̊w�I�ȊW���ʑ��Ƃ����W���ɂ���Ď��̂悤�ȑ����W�A
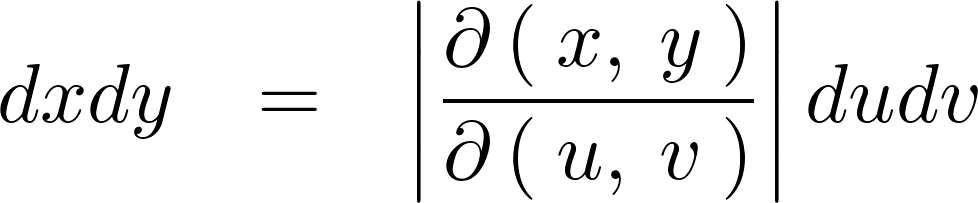
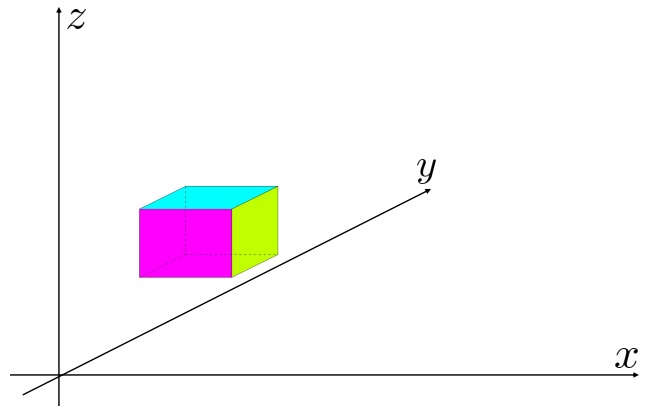
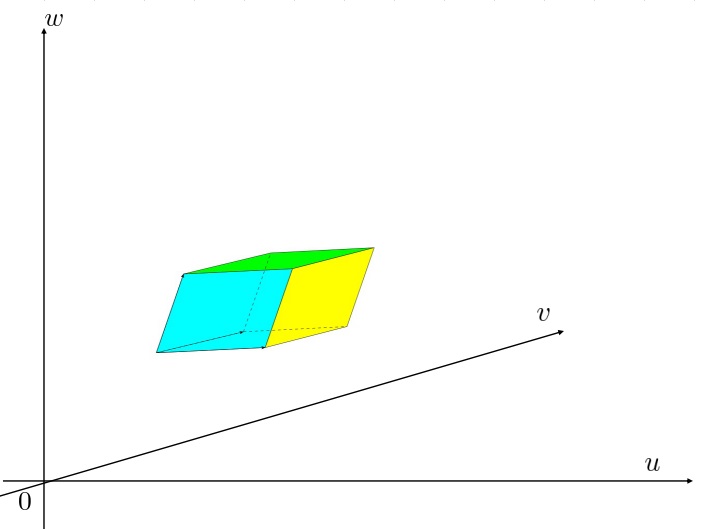
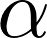
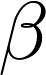
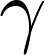
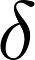
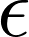

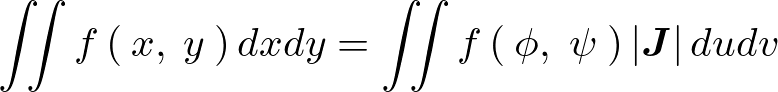
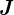 �����̃��R�r�A���ɓ�����B
�����̃��R�r�A���ɓ�����B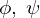 �Ƃ����������l���Ă��̕ϐ���
�Ƃ����������l���Ă��̕ϐ���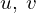 �ƒu���A���ꂪ
�ƒu���A���ꂪ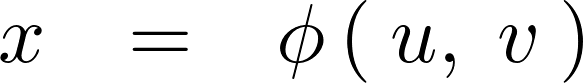
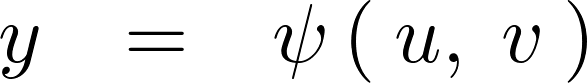
 ���ʏ�̓_
���ʏ�̓_ ���ʏ��
���ʏ��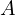 ���N�_�ɂ������̒���
���N�_�ɂ������̒���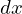 �A�c�̒�����
�A�c�̒�����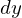 �̒����`�̔����ʐ�
�̒����`�̔����ʐ�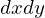 ���l���Ă��̒��_�����ꂼ��
���l���Ă��̒��_�����ꂼ��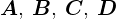 �Ƃ��āA���̂悤�Ȕ����ʐρA
�Ƃ��āA���̂悤�Ȕ����ʐρA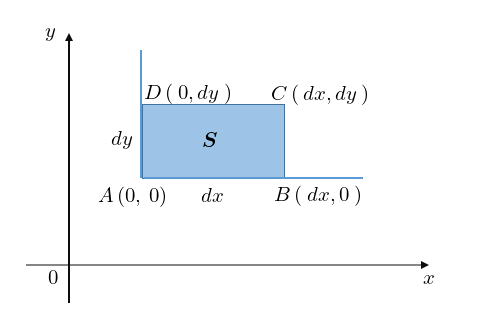
 �ƒu�����Ƃɂ���B
�ƒu�����Ƃɂ���B






















