○解析力学とは、簡単に説明すればニュートン力学における運動方程式の記述を座標変換などの解析的な手法を用い、力学の現象を数学的に洗練された形にあらためて表現しなおしたものをいいます。
解析力学コンテンツ
ラグランジュ運動方程式
運動方程式の一般化Section 0
座標変換の簡単な例━ 【ベクトルの回転変換】
原点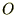
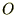を共通にの周りに反時計回りに角度
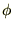だけ回転させた直交座標系を極座標
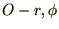座標系とし、元の座標系
座標系との関係。
ベクトル
： 
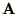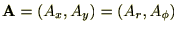
座標変換画像
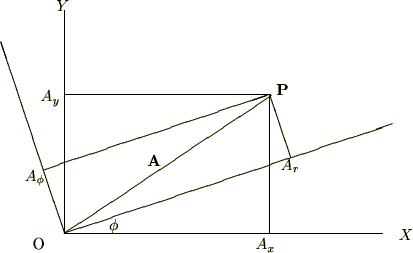
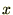座標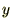
座標を極座標変数
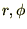で表すと
これを
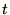（時間）で微分します。
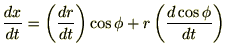
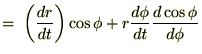
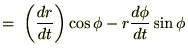
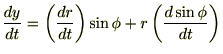
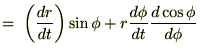
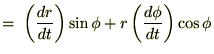
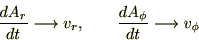
とすれば、
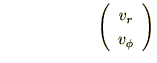
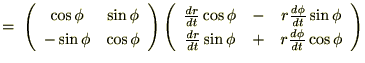
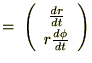
さらに直交座標系における加速度成分を示すと、
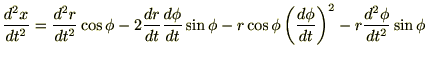
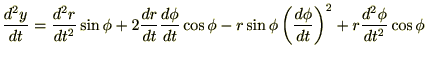
これらより極座標成分による加速度成分を求めると、
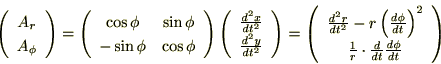
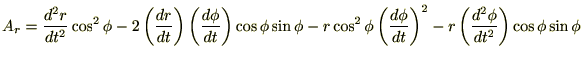
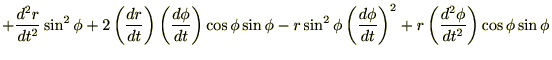
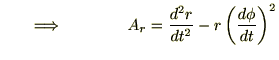
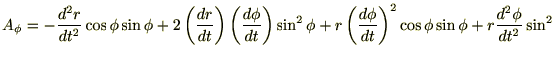
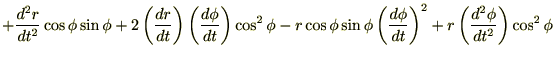
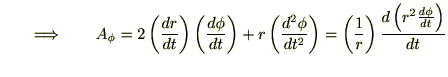
タイトルにでかでかと“解析力学”と書いてますが、内容的にはラグランジュ方程式、オイラー方程式の組み立て方、オイラー式を使った問題などの基本的な部分と、変分原理に関して典型的な事項についてのみ軽く説明してるだけなので、あまり詳しくはやっていません。
あくまで初学者、あるいは一般の方が、解析力学というものはどんなものかと知るような場合に適した内容になっているかと思います。ただしある程度の微分積分学の知識が必要です。
ページの進め方はページの最下部にあるＮＥＸＴボタンをクリックすれば順通りに進むようになっています。
また目的のページ進みたい場合は右サイドバーにある内部リンク、または上部ヘッダー部分にあるメニューボタンを押していただければそのコンテンツページに飛ぶようになっています。それぞれの目的のコンテンツページページへお進みください。
リンクフリーです。こんなサイトでよかったら勝手にリンクしてください。
（＾ω＾）ﾌﾞﾋﾌﾞﾋﾌﾞｰ
