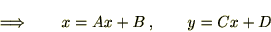�I�C���[������
�I�C���[�̎�
������̐ϕ�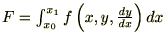 ������Ƃ��܂��B
������Ƃ��܂��B
���̍��ق��l���āA���̎��̕ψʂ�
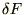 �Ƃ���Ƃ��ꂪ�ɒl���������Ƃ����̂́A
�Ƃ���Ƃ��ꂪ�ɒl���������Ƃ����̂́A
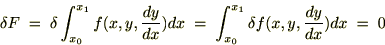
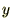 ��������Ƃ��������������̂�
��������Ƃ��������������̂�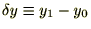 �Ƃ��A���̓���
�Ƃ��A���̓���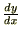 �̕ϕ����Ƃ�ƁA
�̕ϕ����Ƃ�ƁA
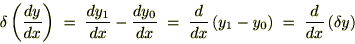
���Ă킩��悤�ɔ����ƕϕ��͓��ꊷ���邱�Ƃ��\�ł��B
�����
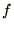 �ɑS�����̌�����K�p����Ǝ��̂悤�ɂȂ�܂��B
�ɑS�����̌�����K�p����Ǝ��̂悤�ɂȂ�܂��B
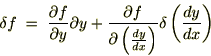
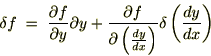 �̎���
�̎��� ��������A
��������A
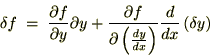
�����
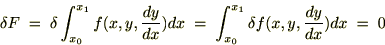 �̎��ɂ����������ƁA
�̎��ɂ����������ƁA
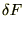
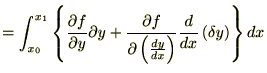
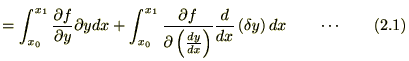
��Q���̌v�Z�͕����ϕ����g���܂��B
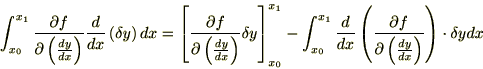
�����ŏ㎮�̕����ϕ����{�����E�ӑ�ꍀ�́A�[�_���Œ�i�����|�C���g�j���Ă���̂Ō��ʂ�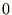 �ɂȂ�܂��B
�ɂȂ�܂��B
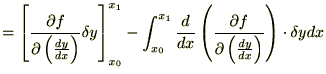
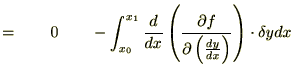
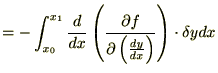

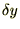 �ɑ��Č���
�ɑ��Č���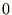 �łȂ���Ȃ�Ȃ��̂�
�łȂ���Ȃ�Ȃ��̂�
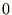 �ɂȂ�܂��B
�ɂȂ�܂��B
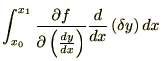
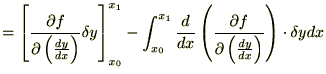
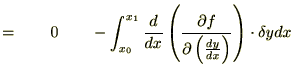
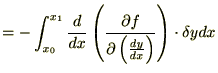
(2.1)�ɑ������A
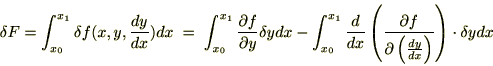

�����Ă��̐ϕ���
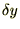 �ɑ��Č���
�ɑ��Č��� �łȂ���Ȃ�Ȃ��̂�
�łȂ���Ȃ�Ȃ��̂�
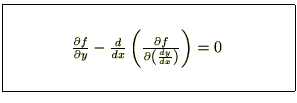
�ƂȂ�܂��B����̓I�C���[�̕������A�܂��̓I�C���[���O�����W���������ƌĂ�Ă�����̂ł��B
���̃I�C���[�E���O�����W���̕������������ĊȒP�ȗ�𑨂��Ă݂܂��傤�B
�ȒP�ȗ�
���ʏ��2�_�����ԋȐ��Œ������ŏ��ɂȂ���̂͒����ł��B���̂��Ƃ��I�C���[�E���O�����W�������g���Ď����Ă݂܂��傤�B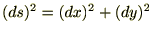 �Ȑ��̃p�����[�^�[�Ƃ���
�Ȑ��̃p�����[�^�[�Ƃ���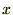 ���Ƃ�A
���Ƃ�A
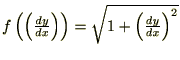 �ɑ���I�C���[�E���O�����W���������́A
�ɑ���I�C���[�E���O�����W���������́A
���v�f�̂Q���
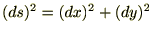 �Ȑ��̃p�����[�^�[�Ƃ���
�Ȑ��̃p�����[�^�[�Ƃ���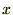 ���Ƃ�A
���Ƃ�A
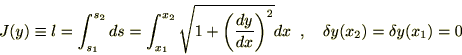
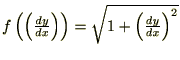 �ɑ���I�C���[�E���O�����W���������́A
�ɑ���I�C���[�E���O�����W���������́A
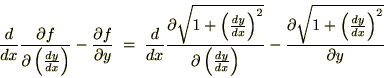

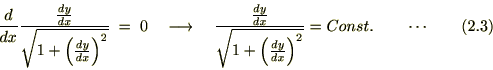
�����(2.3)�́A
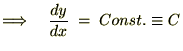
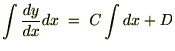

�ƂȂ��͂蒼���ł��邱�Ƃ��킩��܂��B�i�ϕ��萔
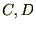 �́A
�́A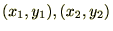 �j
�j
�����ŔC�ӂ̃p�����[�^�[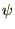 ���Ƃ����ꍇ������Ă݂�ƁA
���Ƃ����ꍇ������Ă݂�ƁA
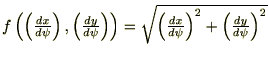 �Ȃ̂ł���ɑ���I�C���[�E���O�����W���������́A
�Ȃ̂ł���ɑ���I�C���[�E���O�����W���������́A
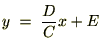
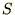 �ɂƂ��
�ɂƂ��
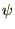 ���Ƃ����ꍇ������Ă݂�ƁA
���Ƃ����ꍇ������Ă݂�ƁA
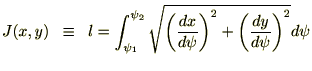
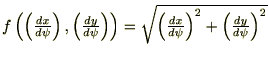 �Ȃ̂ł���ɑ���I�C���[�E���O�����W���������́A
�Ȃ̂ł���ɑ���I�C���[�E���O�����W���������́A
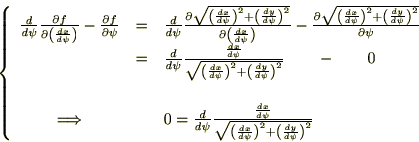
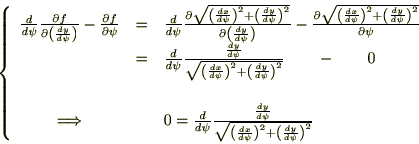
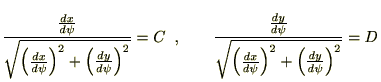
���ӂ�A��������A
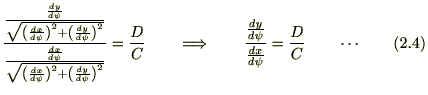
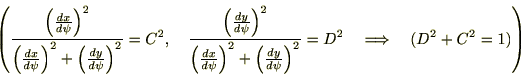
(2.4)�����A
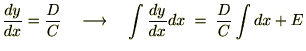
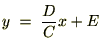
����ɍ��x�̓p�����[�^�[��
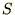 �ɂƂ��
�ɂƂ��
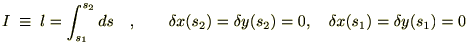
���̎��̃I�C���[�E���O�����W���������͒��ڕϕ��v�Z���s���܂��B
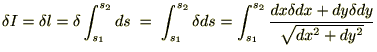
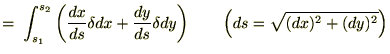
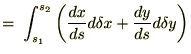
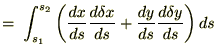
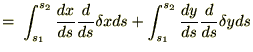
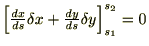 �ł��邱�Ƃɒ��ӂ��A��L�̎��ɕ����ϕ������s����Ǝ��̂悤�ɂȂ�܂��B
�ł��邱�Ƃɒ��ӂ��A��L�̎��ɕ����ϕ������s����Ǝ��̂悤�ɂȂ�܂��B
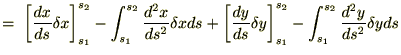
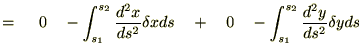
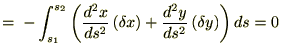
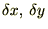 �͔C�ӂ̕ϕ��Ȃ̂ł��ꂼ��A
�͔C�ӂ̕ϕ��Ȃ̂ł��ꂼ��A
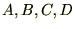 �ƒu���Ă����A
�ƒu���Ă����A
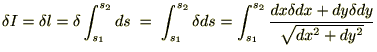
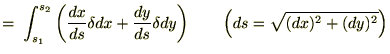
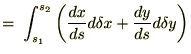
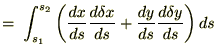
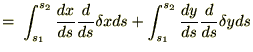
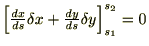 �ł��邱�Ƃɒ��ӂ��A��L�̎��ɕ����ϕ������s����Ǝ��̂悤�ɂȂ�܂��B
�ł��邱�Ƃɒ��ӂ��A��L�̎��ɕ����ϕ������s����Ǝ��̂悤�ɂȂ�܂��B
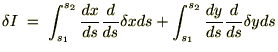
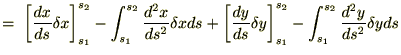
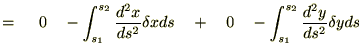
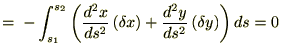
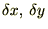 �͔C�ӂ̕ϕ��Ȃ̂ł��ꂼ��A
�͔C�ӂ̕ϕ��Ȃ̂ł��ꂼ��A
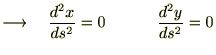
�o�Ă���ϕ��萔��
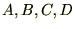 �ƒu���Ă����A
�ƒu���Ă����A