‚¨’m‚点
“–WebƒTƒCƒg‚حƒTƒCƒgچىگ¬ƒVƒXƒeƒ€‚جگ[چڈ‚بŒ‡ٹׂة‚و‚茻چفƒٹƒ“ƒN‚ج•دچX‚ًچs‚ء‚ؤ‚¨‚è‚ـ‚·پBٹا—گl‚ھ‘½–Z‚ج‚½‚كƒٹƒ_ƒCƒŒƒNƒgƒTƒCƒg‚حچىگ¬‚¹‚¸پA’¼گعƒٹƒ“ƒN•دچX‚ًچs‚¤—\’è‚إ‚·پB‰½‘²‚²—¹ڈ³‚‚¾‚³‚¢پBژٹْ‚ح–¢’è‚ة‚ب‚è‚ـ‚·پB
ٹù‘¶‚جƒyپ[ƒW‚ح‚ب‚é‚ׂژc‚·‚و‚¤‚ة‚µ‚ـ‚·‚ھ’¼‚إ•دچX‚µ‚ـ‚·‚ج‚إƒuƒbƒNƒ}پ[ƒN‚ب‚ا‚µ‚ؤ‚¢‚é•û‚حپA‚²–ت“|‚ة‚ب‚é‚©‚ئژv‚¢‚ـ‚·‚ھ‚±‚جƒhƒپƒCƒ“https://mathematical.jp/mathematical/پ@‚©‚ç–ع“I‚جƒyپ[ƒW‚ةچs‚‚و‚¤‚ة‚¨ٹè‚¢گ\‚µڈم‚°‚ـ‚·پB
‘o‹بگüٹضگ”‚جƒ‰ƒvƒ‰ƒX•دٹ·
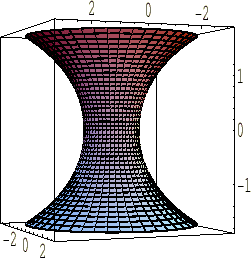
‘o‹بگüٹضگ”‚ئ‚ح
ƒچپ[ƒv‚âژ…‚ب‚ا‚ج‚ذ‚à‚ج—ق‚ًپA‚»‚ج—¼’[‚ًŒإ’肵‚ؤ‚آ‚肳‚°‚½‚à‚ج‚ةŒœگ‚گü‚ئŒؤ‚خ‚ê‚é‚à‚ج‚ھ‚ ‚è‚ـ‚·پB‚±‚ê‚ح•¨—“I‚بƒ|ƒeƒ“ƒVƒƒƒ‹‚ھچإڈ¬‚ة‚ب‚é‚ئ‚«‚ج‚à‚ج‚إ‚ ‚èپAژwگ”ٹضگ”‚ج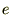 ‚ًژg‚ء‚ؤژں‚ج‚و‚¤‚بژ®‚إ•\‚³‚ê‚ـ‚·پB
‚ًژg‚ء‚ؤژں‚ج‚و‚¤‚بژ®‚إ•\‚³‚ê‚ـ‚·پB
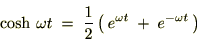
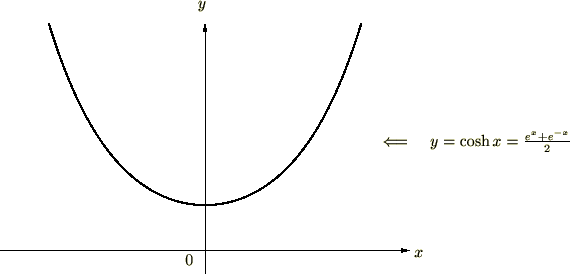
‚±‚ê‚ج“±ڈo‚جژd•û‚حپA‚±‚؟‚ç‚جژo–…ƒTƒCƒg‚ًژQچl‚ة‚µ‚ؤ‚ف‚ؤ‚‚¾‚³‚¢پB
ˆê”ت“I‚ةژOٹpٹضگ”‚ة—ق‚·‚é‚à‚ج‚إ‘o‹بگüٹضگ”‚ئŒؤ‚خ‚ê‚ؤ‚¨‚èپAڈم‹L‚ج‚à‚جˆبٹO‚ة‚حژں‚ج‚و‚¤‚ب‚à‚ج‚à‚ ‚è‚ـ‚·پB
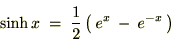
چ،‰ٌ‚ح‚±‚ج‘o‹بگüٹضگ”‚ئ‚¢‚¤‚ج‚ًƒ‰ƒvƒ‰ƒX•دٹ·‚µ‚½‚ç‚ا‚ج‚و‚¤‚بŒ‹‰ت‚ھ‚إ‚é‚©‚ً‚â‚ء‚ؤ‚ف‚ـ‚µ‚½پB
cosh(ƒRƒbƒVƒ…)‚جƒ‰ƒvƒ‰ƒX•دٹ·
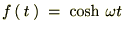 ‚جڈêچ‡پA
‚جڈêچ‡پA
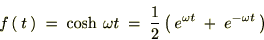
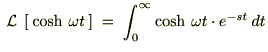
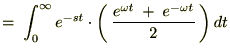
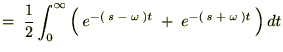
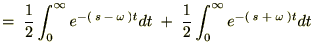
’uٹ·گد•ھ
‚±‚±‚إپAڈم‹Lژ®‚ًگد•ھ‚µ‚â‚·‚‚·‚邽‚ك‚ةپAژwگ”•”•ھ‚ًژں‚ج‚و‚¤‚ة’u‚«ٹ·‚¦‚ـ‚·پB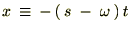
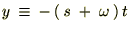
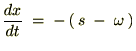
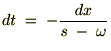
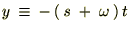 ‚جژ®‚à“¯—l‚ة‚µ‚ؤپA
‚جژ®‚à“¯—l‚ة‚µ‚ؤپA
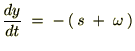
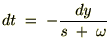
‚ئ‚ب‚é‚ج‚إژں‚ج‚و‚¤‚ة•دٹ·‚µ‚ؤپA‚»‚ꂼ‚ê‚ًŒvژZ‚µ‚ؤ‚¢‚«‚ـ‚·پB
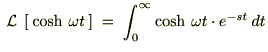
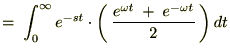
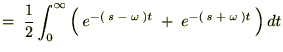
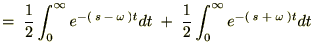
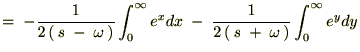
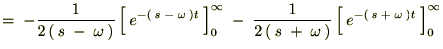
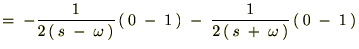
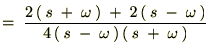
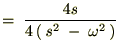
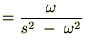
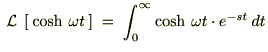
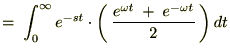
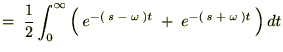
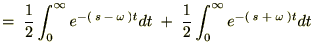
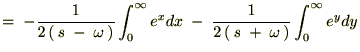
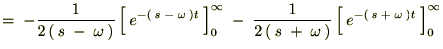
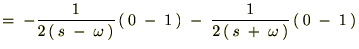
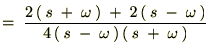
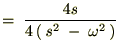
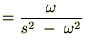
‚و‚ء‚ؤپA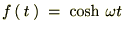 ‚جƒ‰ƒvƒ‰ƒX•دٹ·‚حژں‚ج‚و‚¤‚بŒ`‚ة‚ب‚è‚ـ‚·پB
‚جƒ‰ƒvƒ‰ƒX•دٹ·‚حژں‚ج‚و‚¤‚بŒ`‚ة‚ب‚è‚ـ‚·پB
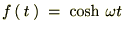 ‚جƒ‰ƒvƒ‰ƒX•دٹ·‚حژں‚ج‚و‚¤‚بŒ`‚ة‚ب‚è‚ـ‚·پB
‚جƒ‰ƒvƒ‰ƒX•دٹ·‚حژں‚ج‚و‚¤‚بŒ`‚ة‚ب‚è‚ـ‚·پB
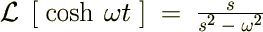

<پiپLپKƒضپKپMپGپjة
ƒ‰ƒvƒ‰ƒX•دٹ·‡DٹضکAƒyپ[ƒW
- ƒ‰ƒvƒ‰ƒX•دٹ·‡F
- گ”ٹwŒnƒuƒچƒOŒ^WebƒRƒ“ƒeƒ“ƒc’u‚«ڈê‚إ‚·پB‚¨‚à‚ة•¨—گ”ٹw‚ًƒپƒCƒ“‚ةˆµ‚¢‚ـ‚·‚ھگV‹KƒTƒCƒg—p‚ةچىگ¬‚µ‚½ƒhƒ‰ƒtƒgƒRƒ“ƒeƒ“ƒc‚à‚ ‚è‚ـ‚·پB
ƒhƒپƒCƒ“’¼‰؛‚جƒRƒ“ƒeƒ“ƒcچXگV‚ح‘ه‘جˆê‚©Œژ‚©‚甼”N‚®‚ç‚¢‚ة1‹Lژ–‚ ‚½‚è‚ة‚ب‚é‚ئژv‚¢‚ـ‚·‚ھٹا—گl‚ھ‘½–Z‚بڈêچ‡‚ح‚»‚êˆبڈم‚ةگL‚ر‚ـ‚·پB‚»‚ج‚ئ‚±‚ë‚ً‰½‘²‚²—¹ڈ³‚‚¾‚³‚¢‚ـ‚·‚و‚¤‚و‚낵‚‚¨‚ب‚ھ‚¢‚µ‚ـ½ذہق<پMپحپL> - ƒ‰ƒvƒ‰ƒX•دٹ·‡E
- گ”ٹwŒnƒuƒچƒOŒ^WebƒRƒ“ƒeƒ“ƒc’u‚«ڈê‚إ‚·پB‚¨‚à‚ة•¨—گ”ٹw‚ًƒپƒCƒ“‚ةˆµ‚¢‚ـ‚·‚ھگV‹KƒTƒCƒg—p‚ةچىگ¬‚µ‚½ƒhƒ‰ƒtƒgƒRƒ“ƒeƒ“ƒc‚à‚ ‚è‚ـ‚·پB
ƒhƒپƒCƒ“’¼‰؛‚جƒRƒ“ƒeƒ“ƒcچXگV‚ح‘ه‘جˆê‚©Œژ‚©‚甼”N‚®‚ç‚¢‚ة1‹Lژ–‚ ‚½‚è‚ة‚ب‚é‚ئژv‚¢‚ـ‚·‚ھٹا—گl‚ھ‘½–Z‚بڈêچ‡‚ح‚»‚êˆبڈم‚ةگL‚ر‚ـ‚·پB‚»‚ج‚ئ‚±‚ë‚ً‰½‘²‚²—¹ڈ³‚‚¾‚³‚¢‚ـ‚·‚و‚¤‚و‚낵‚‚¨‚ب‚ھ‚¢‚µ‚ـ½ذہق<پMپحپL>

















