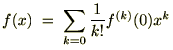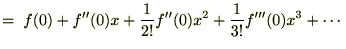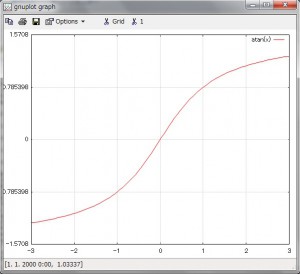
���̂悤�Ȏ��A
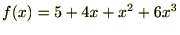
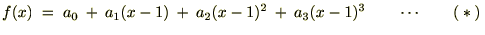
�܂��A�������X�ɔ������Ă����ƁA
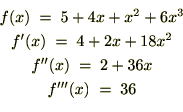
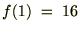
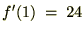
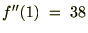
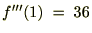
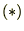 �̎��������P�ƒu���ƁA�܂��A
�̎��������P�ƒu���ƁA�܂��A
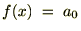
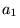 �����߂邽�߂�
�����߂邽�߂�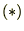 �̎���
�̎���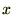 �Ŕ������ĂP��������A
�Ŕ������ĂP��������A
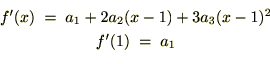
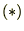 �̎��̔����͍��������g���Ă���A�Ⴆ��
�̎��̔����͍��������g���Ă���A�Ⴆ��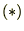 �̑�R���͎��̂悤�ɔ������s���Ă���܂��B
�̑�R���͎��̂悤�ɔ������s���Ă���܂��B
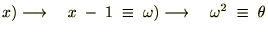
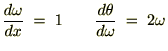
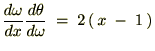
����ɔ������ē����悤�ɂP��������A
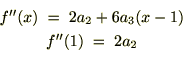
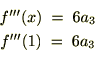
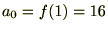
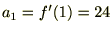
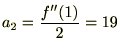
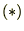 ���͎��̂悤�ɕ\���ł��܂��B
���͎��̂悤�ɕ\���ł��܂��B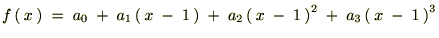
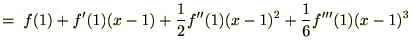
�����܂ł�
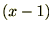 �ɂ��Ă̑������W�J�����܂���������ȊO��
�ɂ��Ă̑������W�J�����܂���������ȊO��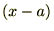 �Ɋւ��Ă����l�ɂȂ�܂��B
�Ɋւ��Ă����l�ɂȂ�܂��B
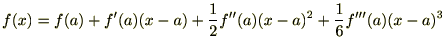
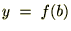
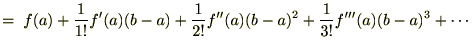
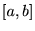 ���܂ފJ��Ԃ�
���܂ފJ��Ԃ�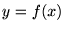 ����
����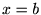 �܂��œW�J����ƌ������肵�܂��B
�܂��œW�J����ƌ������肵�܂��B���Ȃ݂ɕ���ɂ���
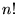 �Ƃ����̂́A�m�̃J�C�W���E�Ƃ�шȉ��̂悤�ɒ�`�������̂ɂȂ�܂��B
�Ƃ����̂́A�m�̃J�C�W���E�Ƃ�шȉ��̂悤�ɒ�`�������̂ɂȂ�܂��B
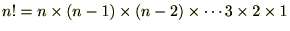
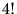 �������ꍇ�A
�������ꍇ�A
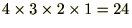
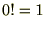
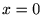 �܂��̃e�C���[����������A����̓}�N���[�����W�J�ȂǂƂ����Ă��܂��B
�܂��̃e�C���[����������A����̓}�N���[�����W�J�ȂǂƂ����Ă��܂��B