���m�点
��Web�T�C�g�̓T�C�g�쐬�V�X�e���̐[���Ȍ��ׂɂ�茻�݃����N�̕ύX���s���Ă���܂��B�Ǘ��l�����Z�̂��߃��_�C���N�g�T�C�g�͍쐬�����A���ڃ����N�ύX���s���\��ł��B�������������������B�����͖���ɂȂ�܂��B
�����̃y�[�W�͂Ȃ�ׂ��c���悤�ɂ��܂������ŕύX���܂��̂Ńu�b�N�}�[�N�Ȃǂ��Ă�����́A���ʓ|�ɂȂ邩�Ǝv���܂������̃h���C��https://mathematical.jp/mathematical/�@����ړI�̃y�[�W�ɍs���悤�ɂ��肢�\���グ�܂��B
�������̓W�J
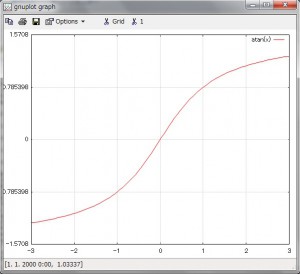
���̂悤�Ȏ��A
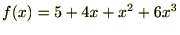
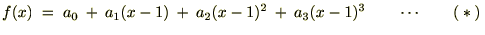
�܂��A�������X�ɔ������Ă����ƁA
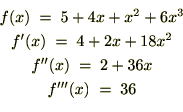
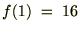
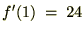
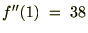
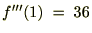
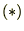 �̎��������P�ƒu���ƁA�܂��A
�̎��������P�ƒu���ƁA�܂��A
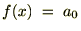
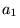 �����߂邽�߂�
�����߂邽�߂�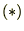 �̎���
�̎���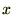 �Ŕ������ĂP��������A
�Ŕ������ĂP��������A
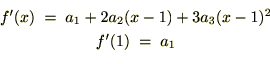
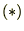 �̎��̔����͍��������g���Ă���A�Ⴆ��
�̎��̔����͍��������g���Ă���A�Ⴆ��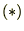 �̑�R���͎��̂悤�ɔ������s���Ă���܂��B
�̑�R���͎��̂悤�ɔ������s���Ă���܂��B
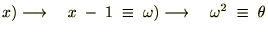
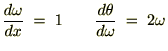
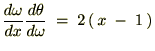
����ɔ������ē����悤�ɂP��������A
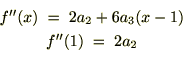
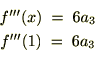
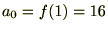
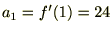
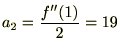
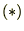 ���͎��̂悤�ɕ\���ł��܂��B
���͎��̂悤�ɕ\���ł��܂��B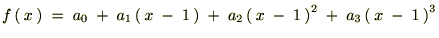
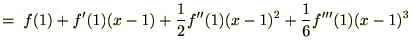
�����܂ł�
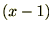 �ɂ��Ă̑������W�J�����܂���������ȊO��
�ɂ��Ă̑������W�J�����܂���������ȊO��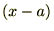 �Ɋւ��Ă����l�ɂȂ�܂��B
�Ɋւ��Ă����l�ɂȂ�܂��B
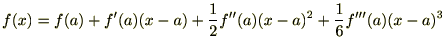
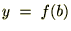
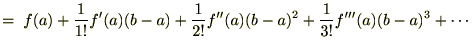
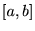 ���܂ފJ��Ԃ�
���܂ފJ��Ԃ�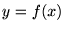 ����
����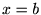 �܂��œW�J����ƌ������肵�܂��B
�܂��œW�J����ƌ������肵�܂��B���Ȃ݂ɕ���ɂ���
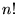 �Ƃ����̂́A�m�̃J�C�W���E�Ƃ�шȉ��̂悤�ɒ�`�������̂ɂȂ�܂��B
�Ƃ����̂́A�m�̃J�C�W���E�Ƃ�шȉ��̂悤�ɒ�`�������̂ɂȂ�܂��B
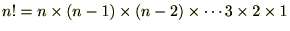
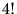 �������ꍇ�A
�������ꍇ�A
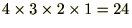
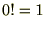
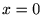 �܂��̃e�C���[����������A����̓}�N���[�����W�J�ȂǂƂ����Ă��܂��B
�܂��̃e�C���[����������A����̓}�N���[�����W�J�ȂǂƂ����Ă��܂��B
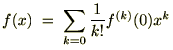
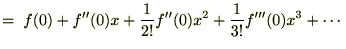
���
���Ɏ�������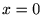 ����ł̃e�C���[�W�J�i�}�N���[�����W�J�j�B
����ł̃e�C���[�W�J�i�}�N���[�����W�J�j�B
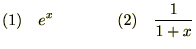
�i�P�j
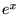 ��
��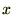 �ł�����������Ă����Ă��������ʂ��o�Ă���̂łO�_�܂��̃e�C���[�W�J
�ł�����������Ă����Ă��������ʂ��o�Ă���̂łO�_�܂��̃e�C���[�W�J
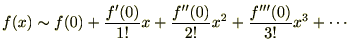
�ɓ��Ă͂߂�Ύ��̂悤�ɂȂ�܂��B
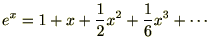
�i�Q�j
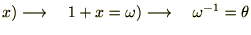
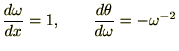
�ȂǂƂ���ĂR�K�����܂ł���Ă����ƁA
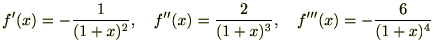
�̂悤�ɂȂ�܂��B����������Ă����A
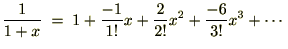
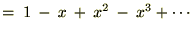
�ݖ�̗�
���Ƃ��Ă͗Ⴆ�Ύ��̂悤�Ȋ����ŏo�肳��邱�Ƃ�����܂��B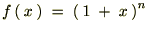 �Ƃ����������������ꍇ�A���̊�
�Ƃ����������������ꍇ�A���̊�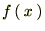 ���3���܂łׂ̂������W�J���ĕ\������A�Ȃ�Ă����ݖ₪�������ꍇ�����Ă��͎��̂悤�Ƀ}�N���[�����W�J���Ė��������Ă������ƂɂȂ�܂��B
���3���܂łׂ̂������W�J���ĕ\������A�Ȃ�Ă����ݖ₪�������ꍇ�����Ă��͎��̂悤�Ƀ}�N���[�����W�J���Ė��������Ă������ƂɂȂ�܂��B

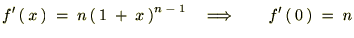
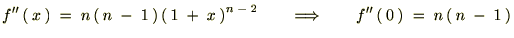
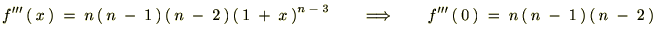
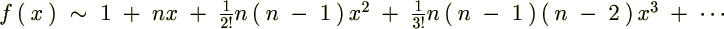
���
���ׂĂ̋������e�C���[�W�J�ł��܂������Ƃ͌���܂���B
�Ⴆ�Ύ��̂悤�Ȏ��������W�J����ꍇ�̓e�C���[�W�J������Ƃ����Ⴒ���Ⴕ�������o�Ă���̂ŕʂ̕��@���g���܂��B
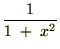
�܂��A
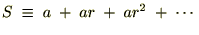
�̂悤�ȋ������l���āA����ɂ���ɒ萔����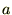 �𗼕ӂɉ��������̂�p���Ď��̂悤�Ȏ����܂��B
�𗼕ӂɉ��������̂�p���Ď��̂悤�Ȏ����܂��B
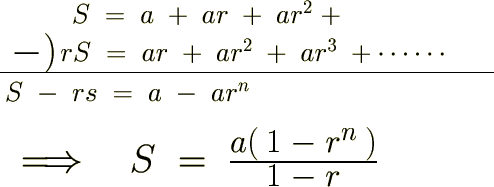
�����ł������Ƃ��ĉ��肷��A
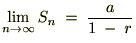
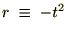 �ƒu���܂��B
�ƒu���܂��B
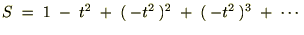
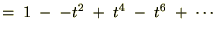
�����ł����Ȃ�łȂ�ł����A���̎��̗��ӂ��O����P�̒�ϕ���������Ǝ��s���Ă݂܂��傤�B
�܂��E�ӂ́A
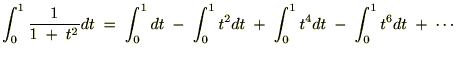
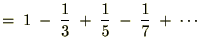
����A���ӂ̐ϕ��Ɋւ��Ăł����A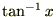 �̔����́A
�̔����́A
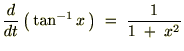
�ł������̂łO����P�܂ł̒�ϕ����s���ƁA
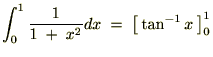
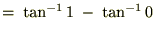
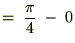
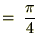
�����ʼnE�̃A�[�N�^���W�F���g�̃O���t���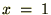 �Ō���邙���̒l�A�O�D�V�W�T�c�Ƃ��������͂R�D�P�S�c��4�Ŋ��������A
�Ō���邙���̒l�A�O�D�V�W�T�c�Ƃ��������͂R�D�P�S�c��4�Ŋ��������A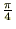 �ɂȂ�܂��B
�ɂȂ�܂��B
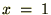 �Ō���邙���̒l�A�O�D�V�W�T�c�Ƃ��������͂R�D�P�S�c��4�Ŋ��������A
�Ō���邙���̒l�A�O�D�V�W�T�c�Ƃ��������͂R�D�P�S�c��4�Ŋ��������A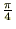 �ɂȂ�܂��B
�ɂȂ�܂��B
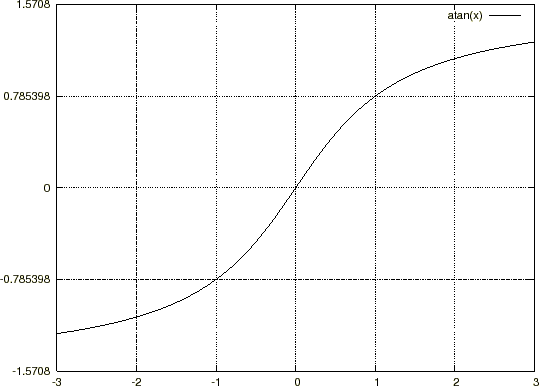
�ƂȂ�̂Ō��ʁA���̂悤�ȊW����������܂��B
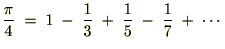
���̎��͌��\�L���Ȑ����炵���A���w�̓ǂݕ��I�ȃe�L�X�g�Ȃł͂��܂ɏЉ��邱�Ƃ�����悤�ł��B
��ʓI�ɂ̓O���S���[�̌����A�܂��̓��C�v�j�b�c�̌����ȂǂƂ����Ă���炵���ł��B
 �@�y�V�i�z�y���ЁE�R�~�b�N ��w�E�Ȋw�E�Z�p�z�I�C���[�̑����@�l�ނ̎���e�ki�l���|1���w�� |

















