���m�点
��Web�T�C�g�̓T�C�g�쐬�V�X�e���̐[���Ȍ��ׂɂ�茻�݃����N�̕ύX���s���Ă���܂��B�Ǘ��l�����Z�̂��߃��_�C���N�g�T�C�g�͍쐬�����A���ڃ����N�ύX���s���\��ł��B�������������������B�����͖���ɂȂ�܂��B
�����̃y�[�W�͂Ȃ�ׂ��c���悤�ɂ��܂������ŕύX���܂��̂Ńu�b�N�}�[�N�Ȃǂ��Ă�����́A���ʓ|�ɂȂ邩�Ǝv���܂������̃h���C��https://mathematical.jp/mathematical/�@����ړI�̃y�[�W�ɍs���悤�ɂ��肢�\���グ�܂��B
���v���V�A���̋ɍ��W�ϊ��ւ̋�̓I�Ȍv�Z

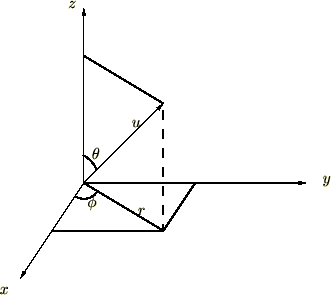

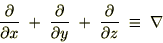
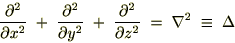
�O��܂ł�2�����v�f�̍�p�f����]���W�n�ɂ����Ăǂ̂悤�ɕό`���邩���l�@���܂��������x�͂��̃��v���V�A���̕\�L���A��]���W�n�ɂ����Ăǂ̂悤�ɕ\���ł���̂����l�@���܂��B
�܂��ŏ���3�����̍��W�n��2�����̂ӂ��ɕ����čl���܂��B��L�̎O�������W�n�̊W���A
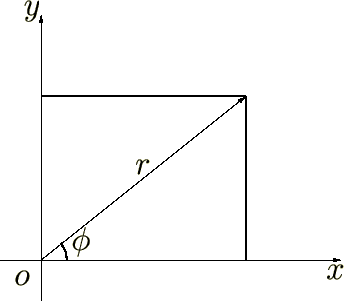
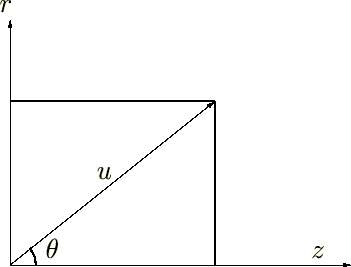

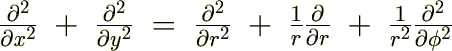
���ɉE�̍��W�n�ɂ�����f�J���g���W�ł̍�p�f�A
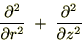
��L��
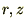 ���W�n�ɂ�����I�y���[�^�[�����W����
���W�n�ɂ�����I�y���[�^�[�����W����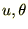 �ł̃I�y���[�^�[�ɕϊ����܂��B
�ł̃I�y���[�^�[�ɕϊ����܂��B�܂��ꎟ�ߎ��ɂ�莟�̂悤�ɑS�������{���܂��B
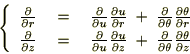
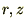 �ɂ���ĕΔ������s���܂��B
�ɂ���ĕΔ������s���܂��B
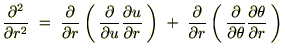
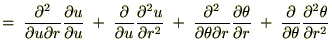
�����ŏ�L���̑�P���Ƒ�Q����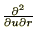 ��
��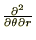 ��
��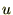 ��
��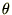 �Ń`�F�[�������܂��B
�Ń`�F�[�������܂��B
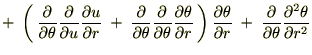
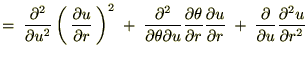
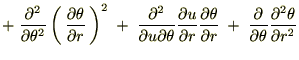
���l�ɂ���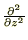 �̂ق��������悤�Ɍv�Z���Ă����Ǝ��̂悤�ɋ��܂�܂��B
�����ō��W�}���A
�̂ق��������悤�Ɍv�Z���Ă����Ǝ��̂悤�ɋ��܂�܂��B
�����ō��W�}���A
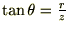 �Ɋւ��Ă͂܂�
�Ɋւ��Ă͂܂�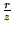 ��
��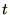 �ƒu�������
�ƒu�������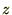 �Ŕ������܂��B
�Ŕ������܂��B
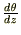 ��
��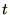 �Ń`�F�[�������܂��B
�Ń`�F�[�������܂��B
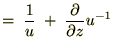
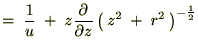
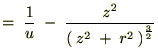
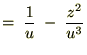
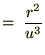
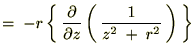
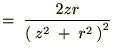
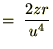
����Ď��̂悤�ɋ��܂�܂��B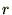 �̕Δ����Ɋւ��Ă����l�Ɍv�Z���Ă����Ύ��̂悤�ɋ��܂�܂��B
�̕Δ����Ɋւ��Ă����l�Ɍv�Z���Ă����Ύ��̂悤�ɋ��܂�܂��B
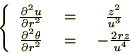
������
�ӁX�������������͂�10��7���̋L���̂悤�Ɏ��̂悤�ɋ��܂�܂��B
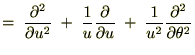
�悤�₭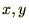 ���W�n�����
���W�n�����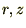 ���W�n�͎��̂悤�ɋ��܂�܂����B
���̗�����ӁX�����������܂��B
���W�n�͎��̂悤�ɋ��܂�܂����B
���̗�����ӁX�����������܂��B
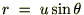 �Ȃ̂ł�����㎮�ɑ�����܂��B
�Ȃ̂ł�����㎮�ɑ�����܂��B
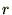 �̃I�y���[�^�[
�̃I�y���[�^�[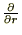 ���������邱�Ƃ��l���܂��B
���������邱�Ƃ��l���܂��B
�܂��I�y���[�^�[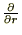 ��
��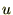 ��
��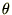 �̑S������
�̑S������
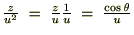
�ł���̂ł�����������A
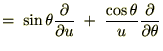
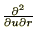 ��
��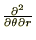 ��
��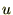 ��
��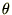 �Ń`�F�[�������܂��B
�Ń`�F�[�������܂��B
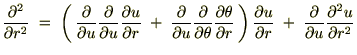
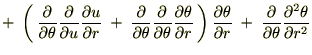
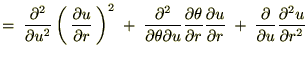
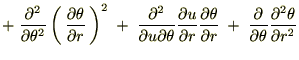
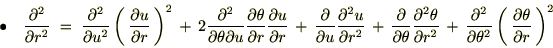
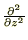 �̂ق��������悤�Ɍv�Z���Ă����Ǝ��̂悤�ɋ��܂�܂��B
�̂ق��������悤�Ɍv�Z���Ă����Ǝ��̂悤�ɋ��܂�܂��B
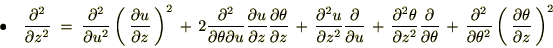
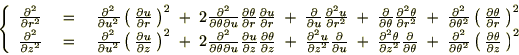
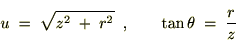
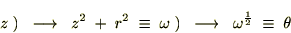
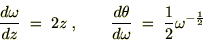
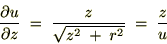
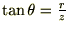 �Ɋւ��Ă͂܂�
�Ɋւ��Ă͂܂�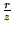 ��
��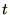 �ƒu�������
�ƒu�������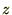 �Ŕ������܂��B
�Ŕ������܂��B


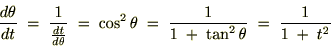
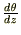 ��
��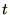 �Ń`�F�[�������܂��B
�Ń`�F�[�������܂��B
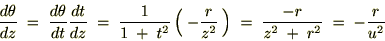
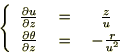
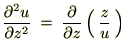
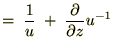
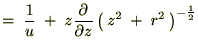
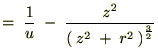
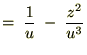
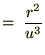
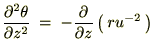
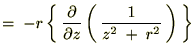
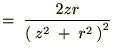
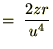
����Ď��̂悤�ɋ��܂�܂��B
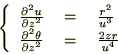
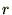 �̕Δ����Ɋւ��Ă����l�Ɍv�Z���Ă����Ύ��̂悤�ɋ��܂�܂��B
�̕Δ����Ɋւ��Ă����l�Ɍv�Z���Ă����Ύ��̂悤�ɋ��܂�܂��B
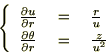
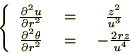
������
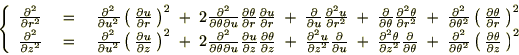
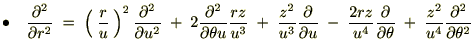
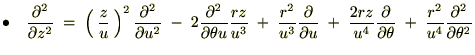
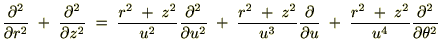
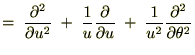
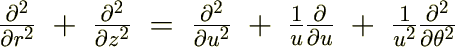
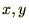 ���W�n�����
���W�n�����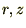 ���W�n�͎��̂悤�ɋ��܂�܂����B
���W�n�͎��̂悤�ɋ��܂�܂����B
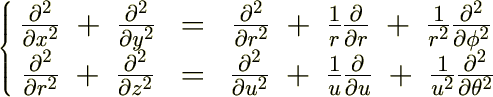
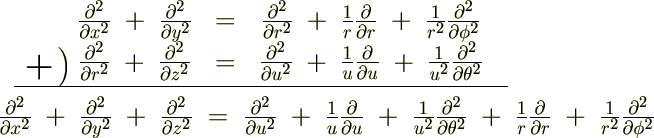
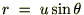 �Ȃ̂ł�����㎮�ɑ�����܂��B
�Ȃ̂ł�����㎮�ɑ�����܂��B
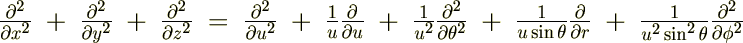
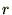 �̃I�y���[�^�[
�̃I�y���[�^�[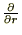 ���������邱�Ƃ��l���܂��B
���������邱�Ƃ��l���܂��B�܂��I�y���[�^�[
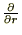 ��
��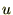 ��
��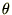 �̑S������
�̑S������
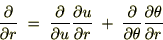
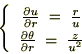
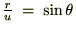
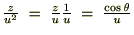
�ł���̂ł�����������A
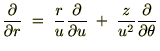
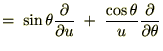
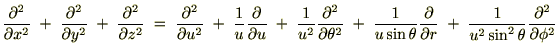
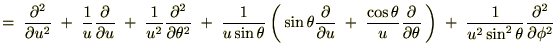
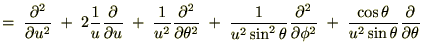
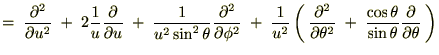
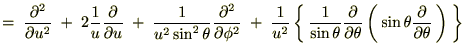
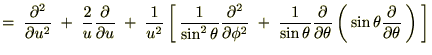
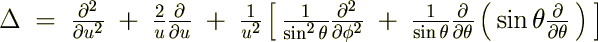
�ɍ��W���v���V�A���֘A�y�[�W
- ���W�ϊ��Q
- �f�J���g���W�ɂ������p�f�i�I�y���[�^�[�j���ɍ��W�ɕϊ�����ߒ����l�@���܂��B
- ���W�ϊ��P
- �f�J���g���W�ɂ������p�f�i�I�y���[�^�[�j���ɍ��W�ɕϊ�����ߒ����l�@���܂��B
- �ɍ��W�̎��Ԕ���
- ��]���W�n�ɂ����鎞�Ԕ������l�@���܂��B
- �ɍ��W�ւ̕ϊ�
- �f�J���g���W����ɍ��W�ցB���̃y�[�W�ł͋ɍ��W�ɂ��^���̋L�q�ɂ��čl�@���܂��B

















