ベクトルの積分
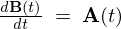 のとき、
のとき、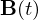 を
を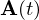 の不定積分といい、
の不定積分といい、
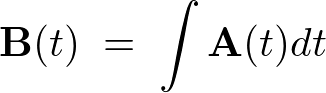
と書きます。
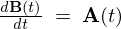 なら、
なら、
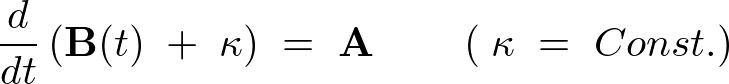
であるので、
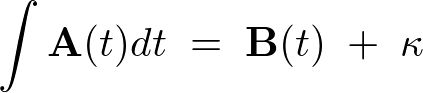
であるといえます。
一般的に、
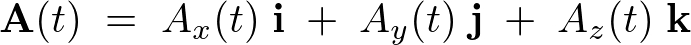
とすれば、
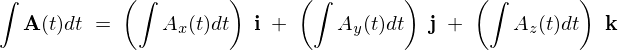
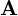 の定積分は、
の定積分は、
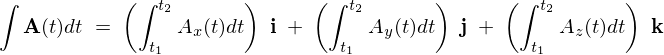
○ベクトル積分に関する重要な性質
以下の公式が重要なものになります。
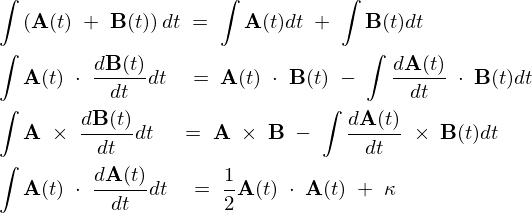
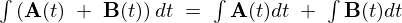 の証明
の証明
まず積の微分公式より、
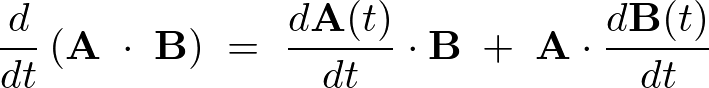
より、
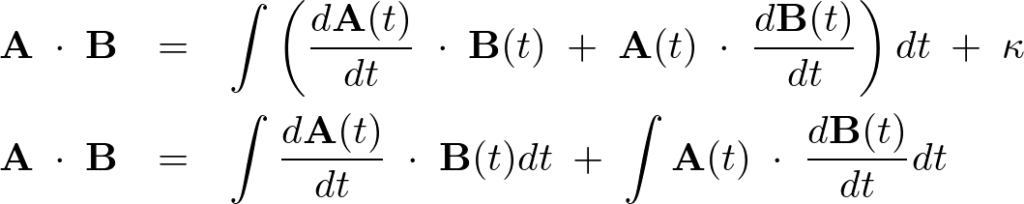
となるので以下のような式が導き出されます。
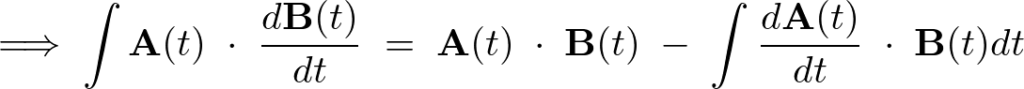
また、
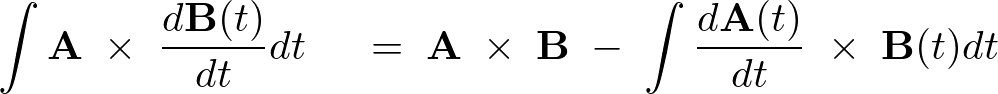
の証明には、この証明を当てはめればよいです。
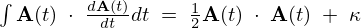 式の証明
式の証明
まず、
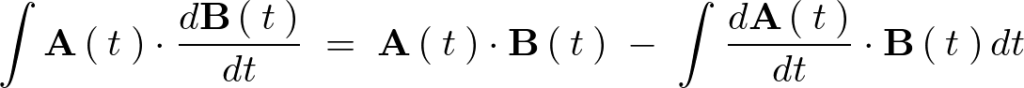
により、
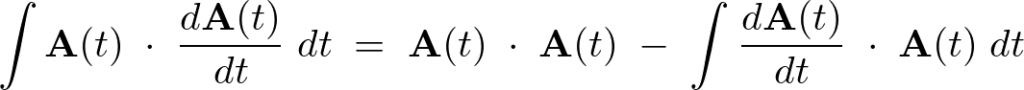
内積は可換なので、
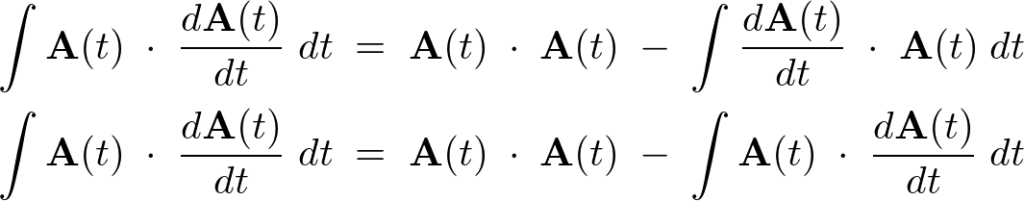
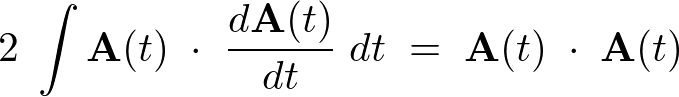
となるので以下のような公式が求まります。
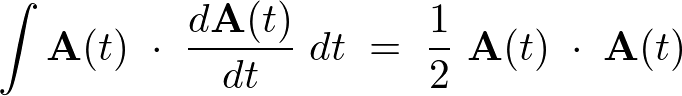
-
diff-eq.comスケールアップアップマイグレーション3
-
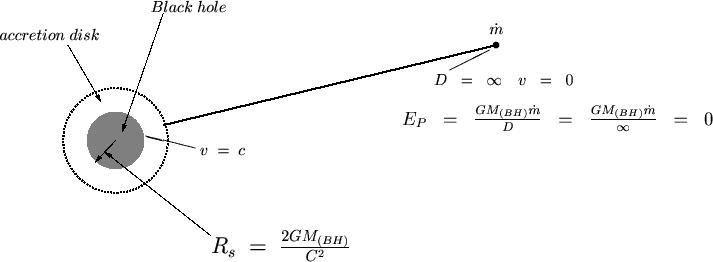
クェーサーとブラックホール
続きを読む
-
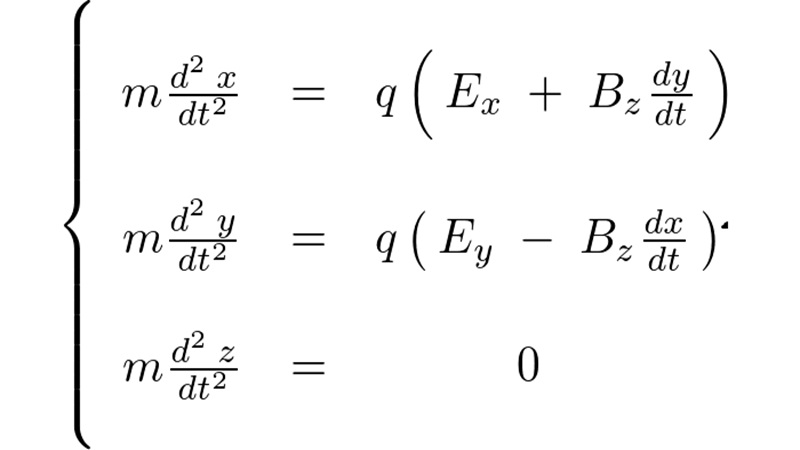
ベクトル解析 ━ 補遺
続きを読む
-
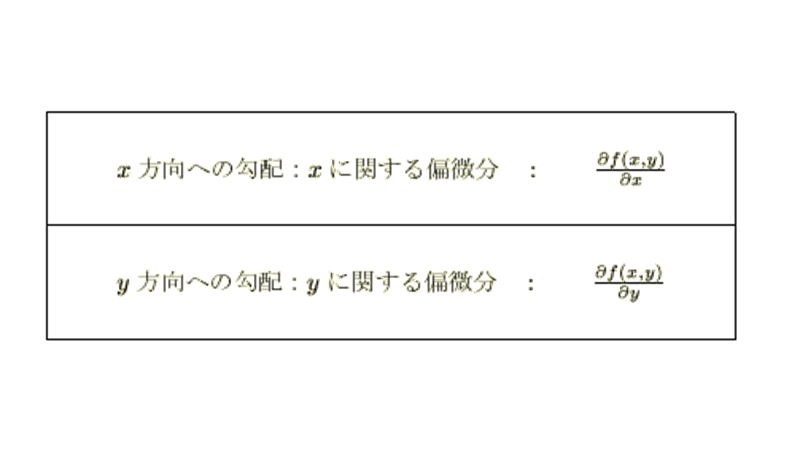
スカラー場、ベクトル場
続きを読む
-
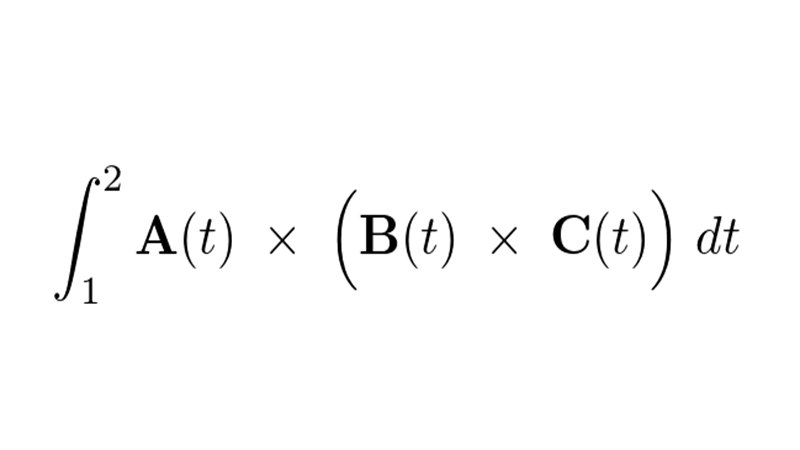
ベクトル積分問題の答え
続きを読む