回帰分析
回帰分析
回帰分析とは、数理統計学の分野において、ある目的変数の変化を説明するために、他の変数、一つの場合は単回帰、複数の説明変数がある場合は重回帰としてその関係性をモデル化する方法になります。
重回帰分析
yを目的変数として説明変数をxとしたとき重回帰モデルの式は複数、少なくとも2つの編回帰係数を持ち単回帰モデルの説明変数が一つなのに対しこの重回帰モデルは説明変数を2つ以上をとります。一つの目的変数を複数の説明変数によって相関関係により導きます。
ここでは重回帰分析において出てくる残渣や回帰係数、編回帰係数などのその数理的な意味合いと導出について詳しく考察していきます。
-
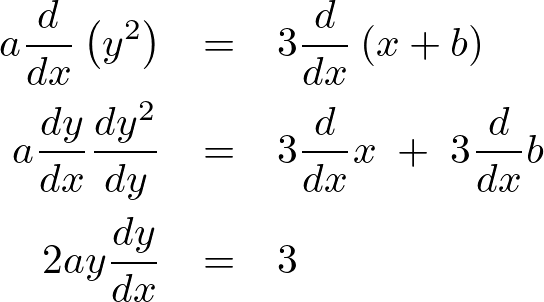
微分方程式いろいろTOPページLaTeXコード
カテゴリー
-
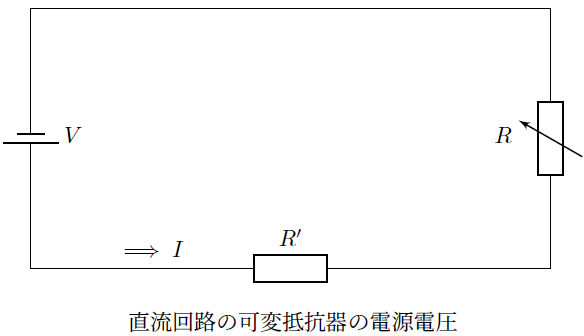
可変抵抗器の直列回路
カテゴリー
-
Cisco Packet Tracer
カテゴリー
-
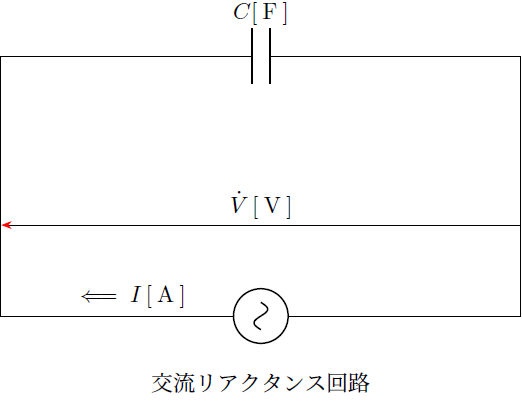
交流回路
カテゴリー
-
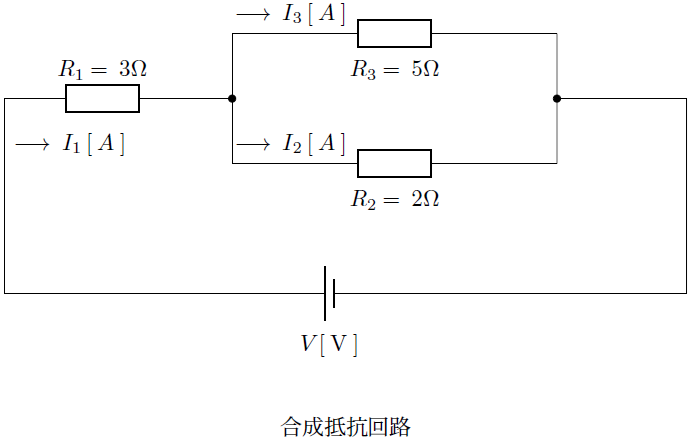
直流回路の合成抵抗
カテゴリー
-
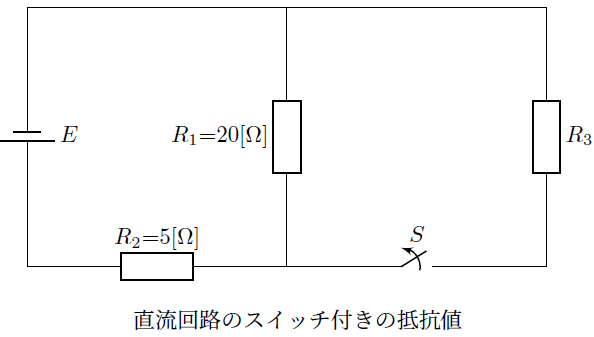
スイッチ付き回路素子の抵抗値
カテゴリー
