ベクトルの微分
ベクトルの微分
ベクトルの時間微分に関して
時間![]() でベクトル
でベクトル![]() の成分ごとに微分をします。
の成分ごとに微分をします。
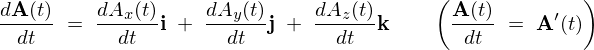
上記式をベクトル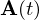 の時刻
の時刻![]() における微分係数と呼びます。
における微分係数と呼びます。
【ベクトルの微分における重要な公式】
以下において![]() を定ベクトル、
を定ベクトル、![]() を定スカラーとします。
を定スカラーとします。
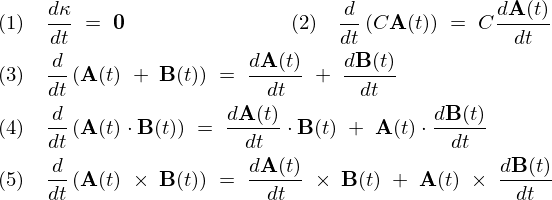
(4)の証明
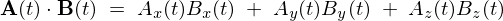
これを![]() で微分すると、
で微分すると、
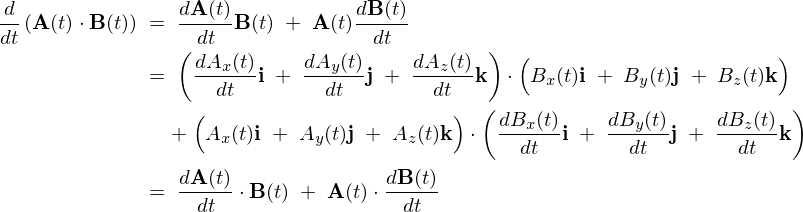
よって、
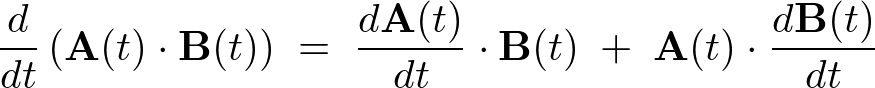
(5)の証明
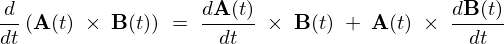
まず最初に、
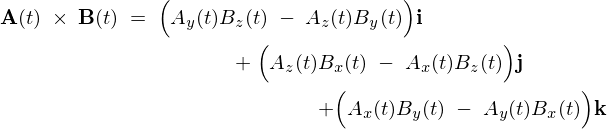
これによって、
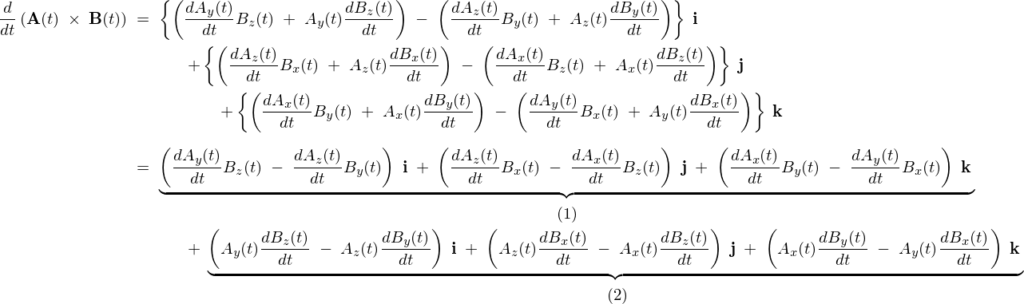
上記の結果により以下のように導かれます。

ベクトル微分に関する重要な性質
内積の時間微分

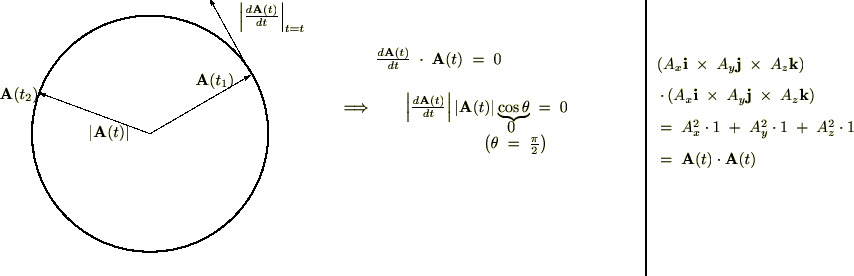
【証明】
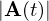 が一定。
が一定。
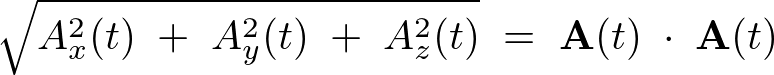
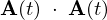 が一定なのでその時間微分は、
が一定なのでその時間微分は、
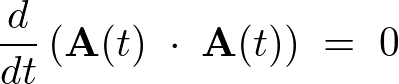
ここで、
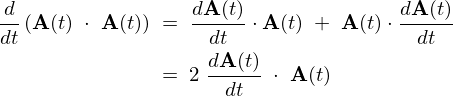
よって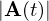 ならば、
ならば、
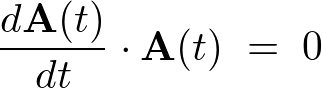
この結果により、 と
と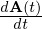 は直行しているということがいえます。
は直行しているということがいえます。
外積の時間微分
次の値を示す2つのベクトル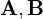 があったとします。
があったとします。
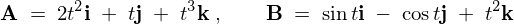
これの外積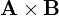 に対する時間微分をやってみましょう。
に対する時間微分をやってみましょう。
まず、
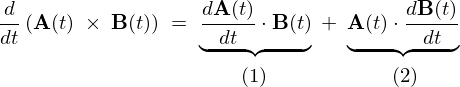
より、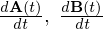 のそれぞれの計算を実行します。
のそれぞれの計算を実行します。
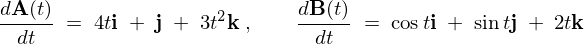
こららより、
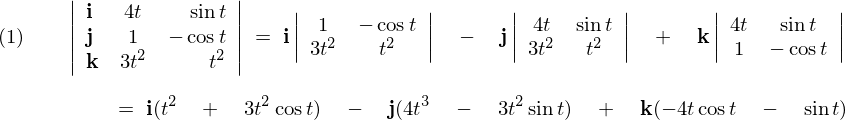
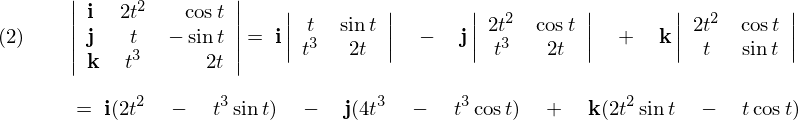
よってこれらの結果より、
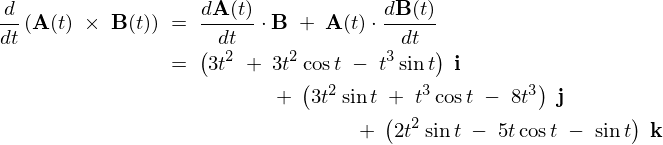

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
-
diff-eq.comスケールアップアップマイグレーション3
-
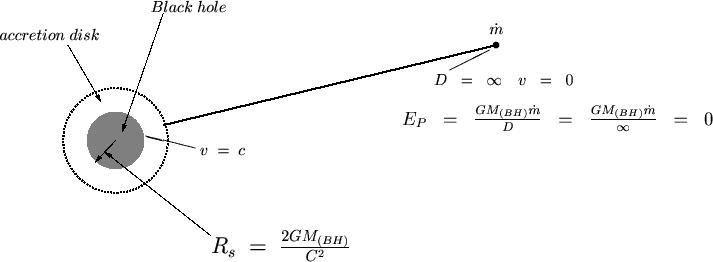
クェーサーとブラックホール
続きを読む
-
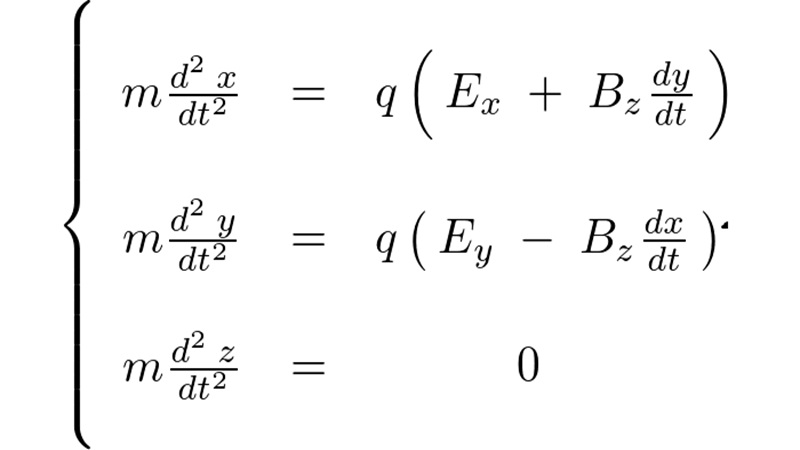
ベクトル解析 ━ 補遺
続きを読む
-
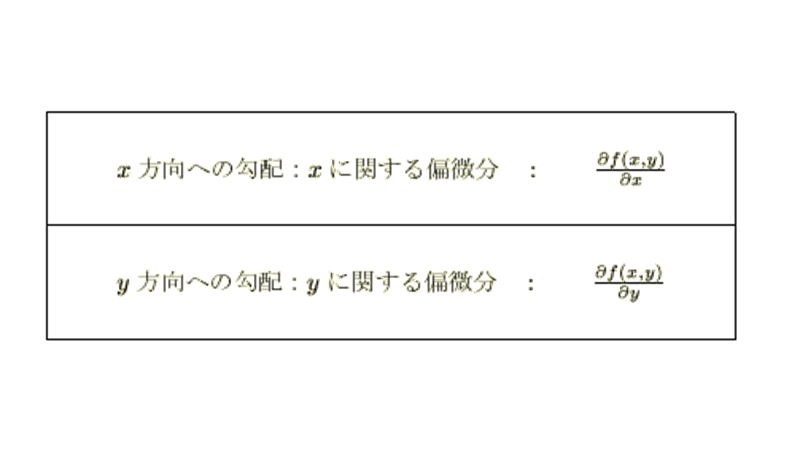
スカラー場、ベクトル場
続きを読む
-
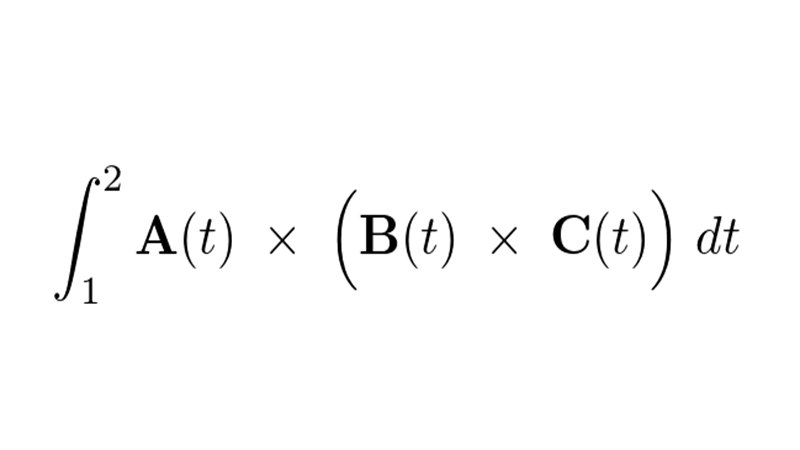
ベクトル積分問題の答え
続きを読む