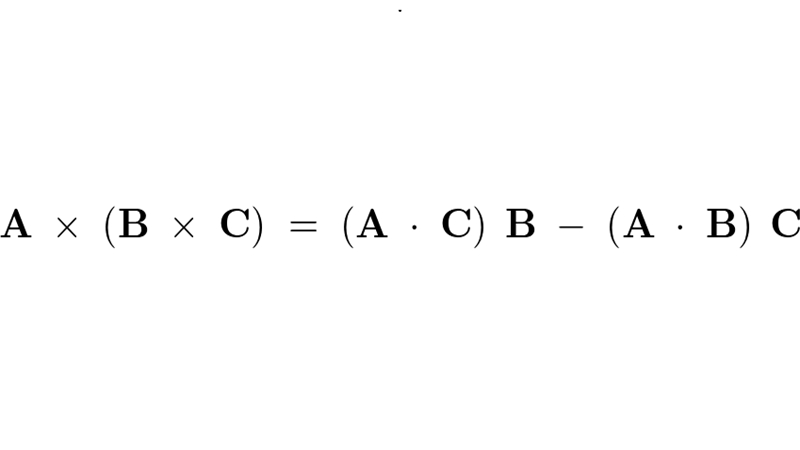ベクトル三重積
ベクトル三重積 ━ その計算過程と証明
先ほどのセクションに出てきた3つのベクトル、
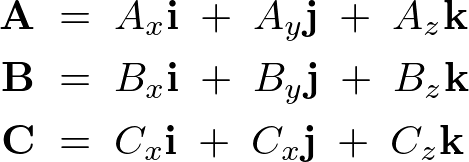
を、このセクションにおいても同じように考えます。
こうしたとき今度は次に示すような“ベクトル三重積”という公式が成り立ちます。
ベクトル三重積公式
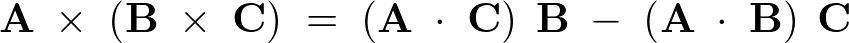
これを実際に証明してみましょう。
まず、![]() と置いて、
と置いて、
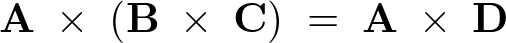
とします。
すると、
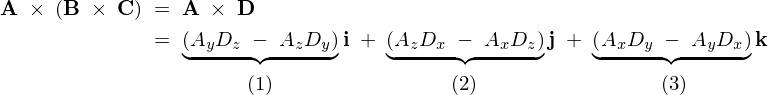
(1)に関して
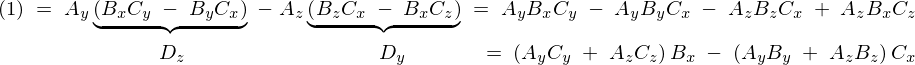
ここで第一項のカッコの中に![]() を、第二項のカッコの中に
を、第二項のカッコの中に![]() を入れても全体の結果は変わりません。
を入れても全体の結果は変わりません。
なので、
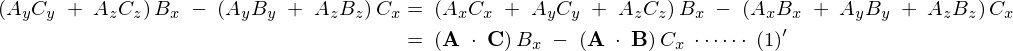
最後のほうは内積の公式を使っています。
続いて![]() のほうも同じように計算していきましょう。
のほうも同じように計算していきましょう。
(2)に関して
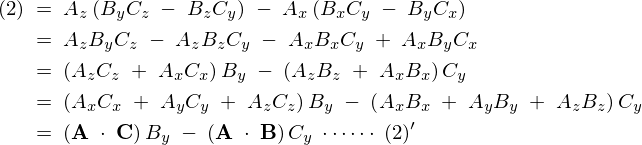
(3)に関して
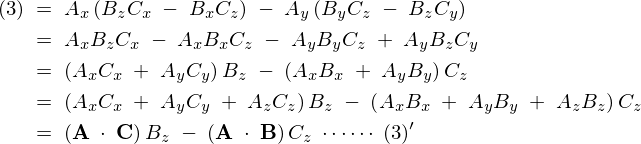
上記の(1)(2)(3)まとめると次のようになります。
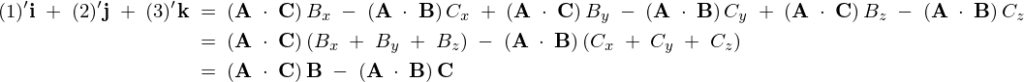
これによって、以下の関係が証明されます。
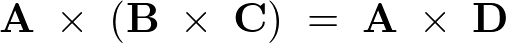

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
-
diff-eq.comスケールアップアップマイグレーション3
-
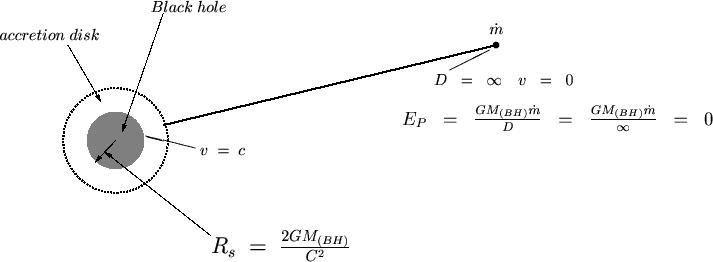
クェーサーとブラックホール
続きを読む
-
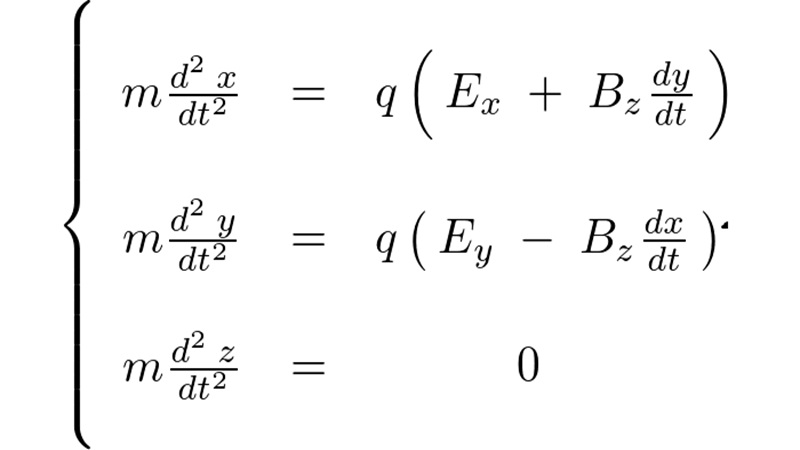
ベクトル解析 ━ 補遺
続きを読む
-
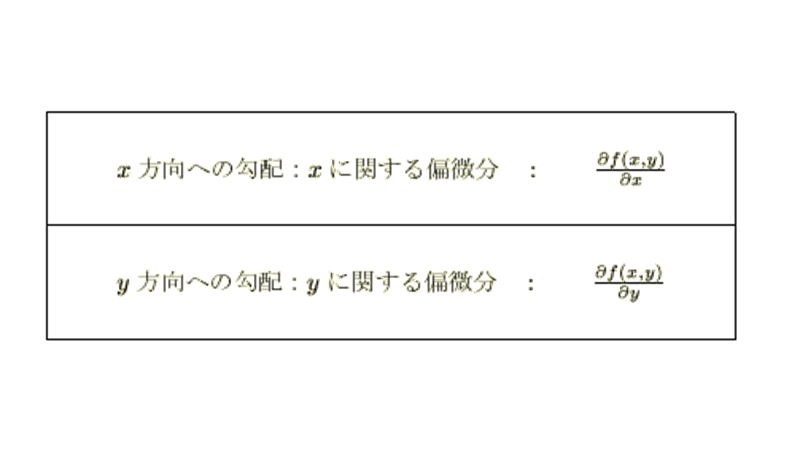
スカラー場、ベクトル場
続きを読む
-
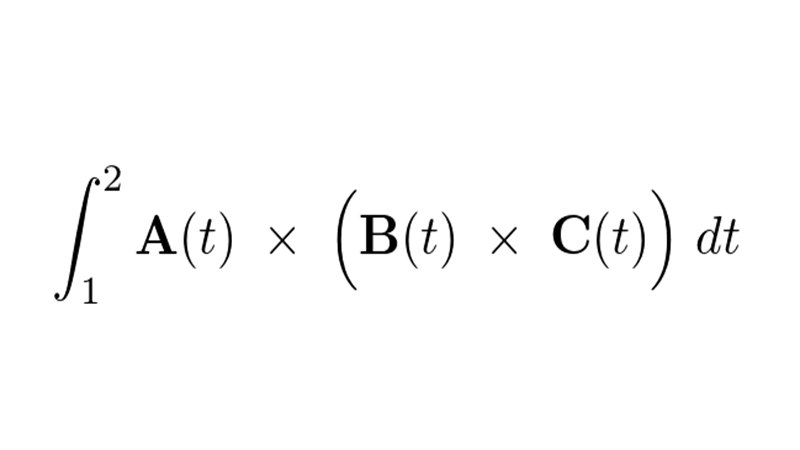
ベクトル積分問題の答え
続きを読む