三次元ベクトル場および発散についての補足
三次元におけるベクトル表現は、
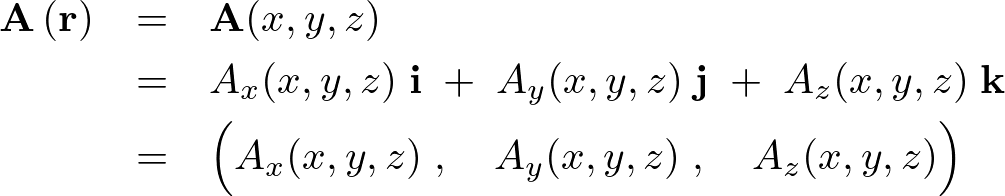
であるので、その発散は次のようになります。
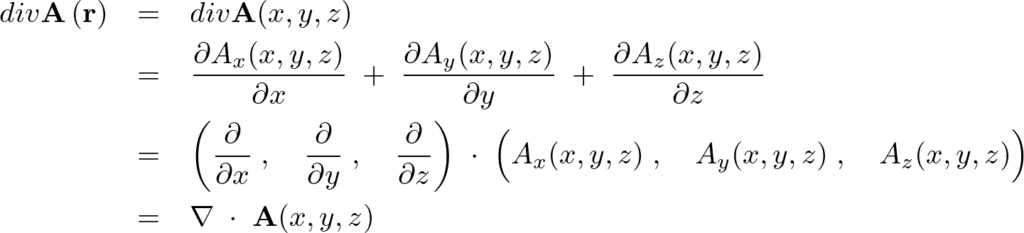
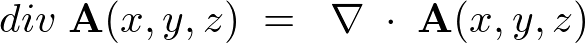
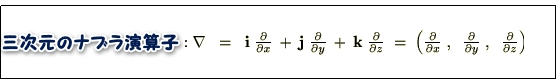
以上のことによりベクトル場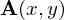 の発散(ダイバージェンス)というのは、
の発散(ダイバージェンス)というのは、
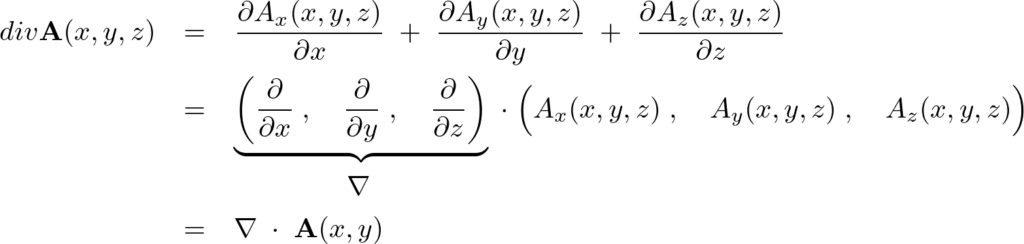
ということなので、

ということがいえます(内積なのでスカラー量)。

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
-
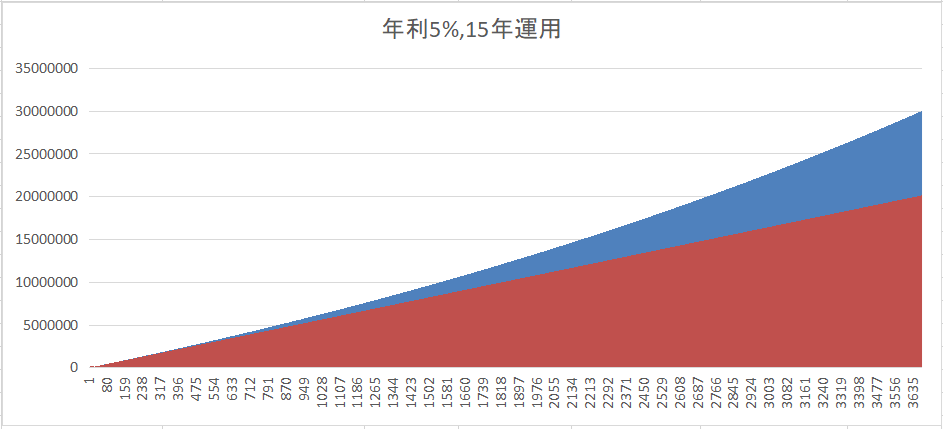
アッパーマス層と年金終価係数
カテゴリー
-
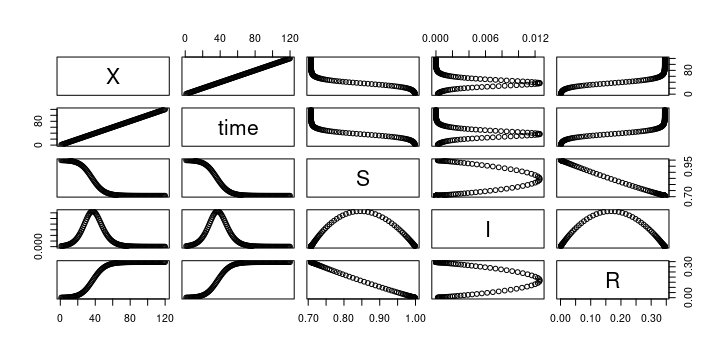
SIRモデル
カテゴリー
-
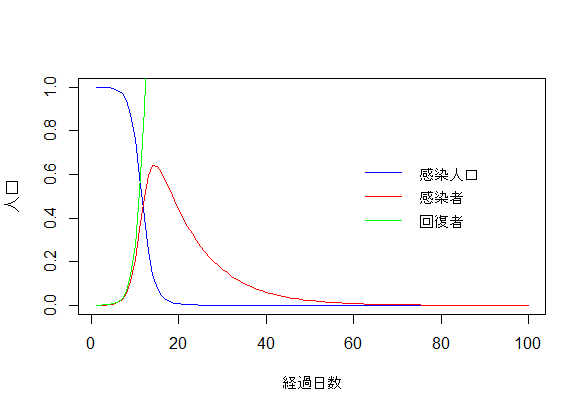
RstudioでSIRモデル②
カテゴリー
-
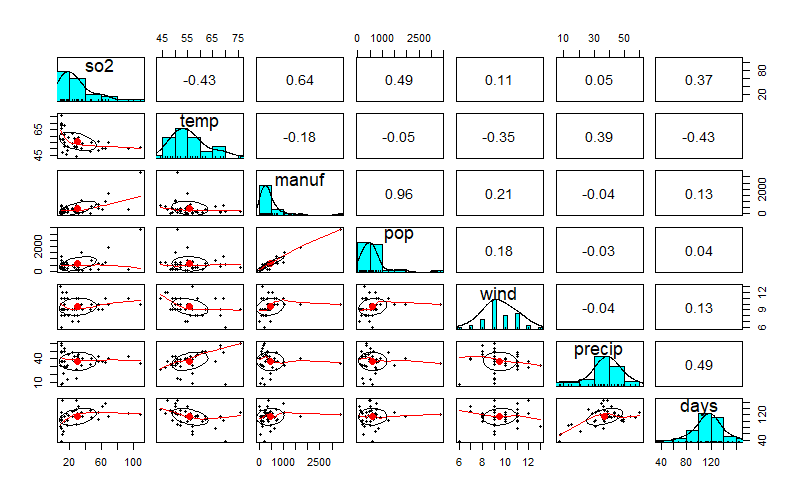
Rで重回帰分析-大気汚染①
カテゴリー
-
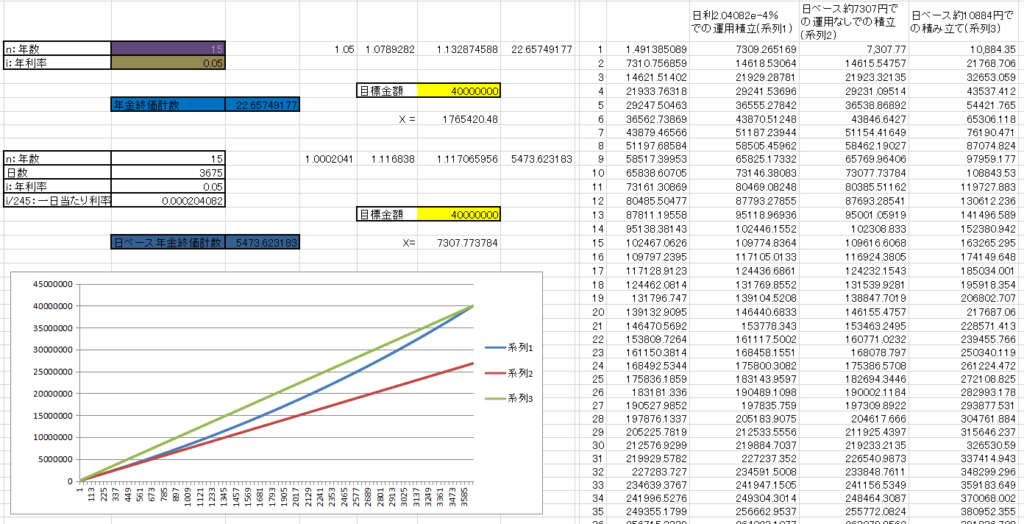
つみたてNISAと年金終価係数
カテゴリー
-
diff-eq.comスケールアップアップマイグレーション4
-
微分方程式いろいろTOPページLaTeXコード
カテゴリー : 微分方程式いろいろLaTeXコードサテライトサイト微分方程式いろいろコンテンツトップページに使われたコードになります。コンパイル時のエラー等の修…
-
-
Cisco Packet Tracer
カテゴリー : Cisco Packet TracerPacket Tracerとは、Ciscoが提供するCisco製のルータやスイッチなどをローカル端末上でコンフ…
-
-
-
-
-
-
-