ベクトル場発散 ━ ダイバージェンス
ある座標点を中心とした領域からのベクトル(矢印)の外向き量を横、縦、別々に考え、それらをその領域の上下、あるいは左右の間隔で割ったものをその座標点からのベクトル場の発散、または“湧き出し”といいます。
二次元ベクトル場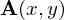 の発散において、ある一つの座標点
の発散において、ある一つの座標点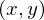 における値は、数学的にはその座標点
における値は、数学的にはその座標点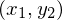 において計算された、
において計算された、
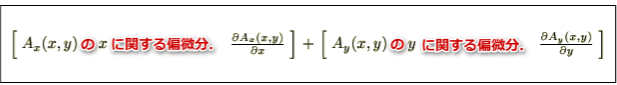
によって与えられます。
さらにはこのベクトル場の発散のことを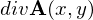 という記号で書きます。
という記号で書きます。
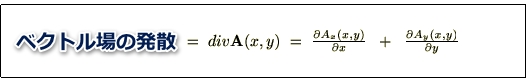
なおこれらは以下のように書き換えることも出来ます。
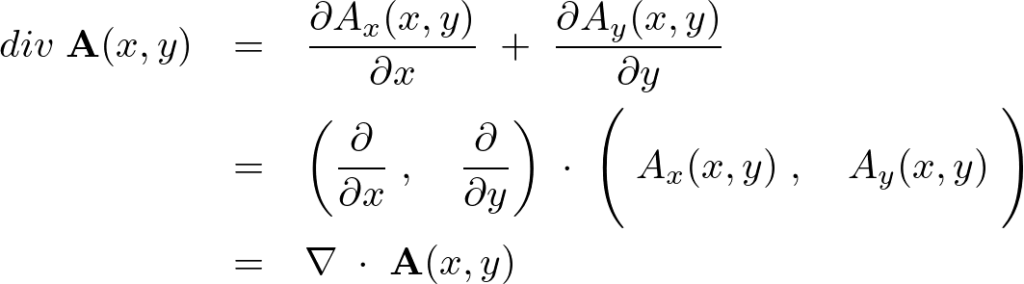
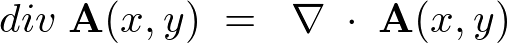
例題①
次に示すようなベクトル勾配があったとします。

このときのベクトル場における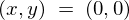 、および
、および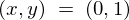 の地点に対するダイバージェンス(ベクトル場の発散)を求めてみましょう。
の地点に対するダイバージェンス(ベクトル場の発散)を求めてみましょう。
まずポイントとする座標点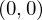 において次のような領域を考えます。
において次のような領域を考えます。

目標とする点を中心に縦横それぞれ2のメモリ幅の領域をとって、そこからの“出っ張り”の部分でのベクトル量をプロットします。
2つのメモリをとっているのでプロットした数字は“2”で割り算をします。
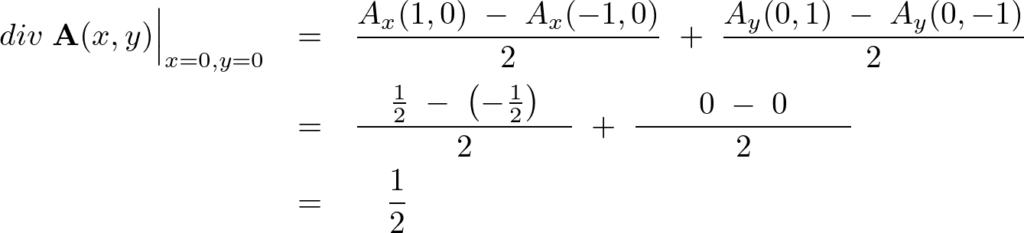
次に、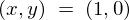 においてのダイバージェンスも先ほどと同じように座標点
においてのダイバージェンスも先ほどと同じように座標点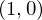 において次のような領域を考えます。
において次のような領域を考えます。

先ほどと同じ要領で計算していきます。
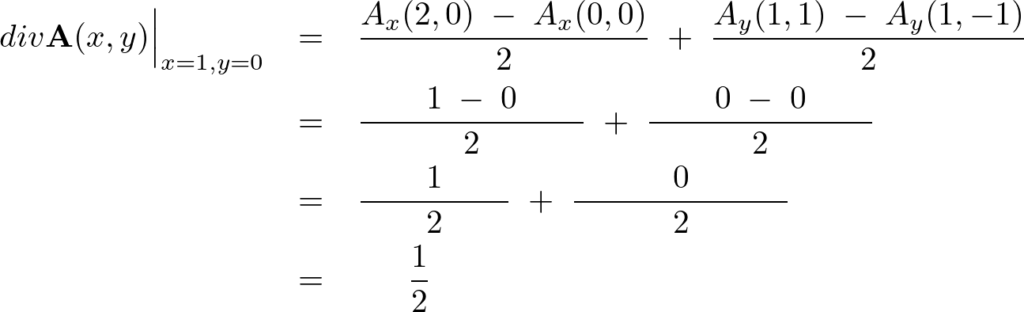
例題②
下のベクトル場において、座標、

のそれぞれにおける![]() (ダイバージェンス)を求めてみましょう。
(ダイバージェンス)を求めてみましょう。
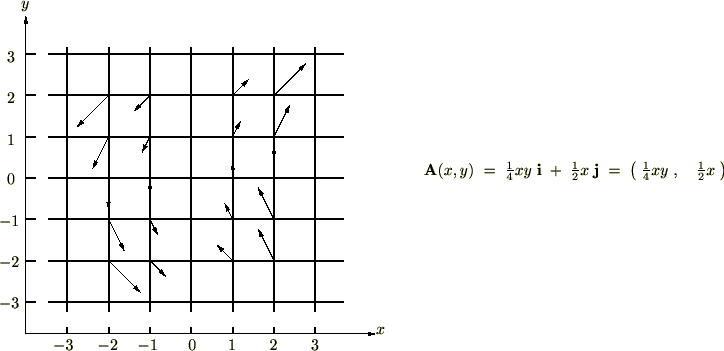
(1)
目的とする座標点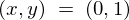 において、次のように例題①で示したような領域を考えます。
において、次のように例題①で示したような領域を考えます。

これを元にダイバージェンスを求めると、
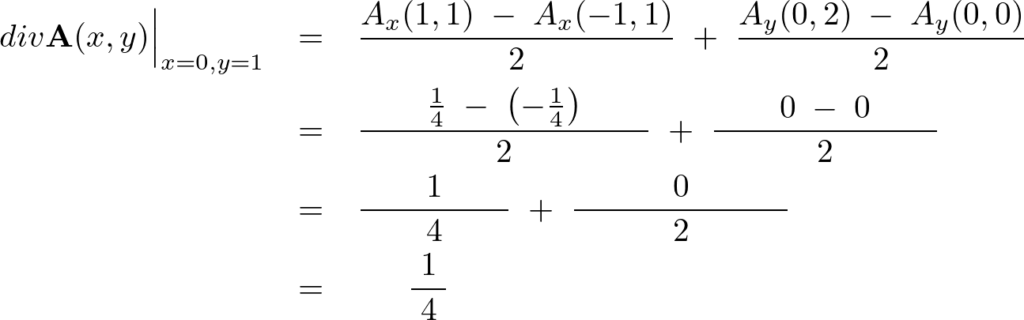
(2)
![]()

上記と同じようにダイバージェンスを求めます。
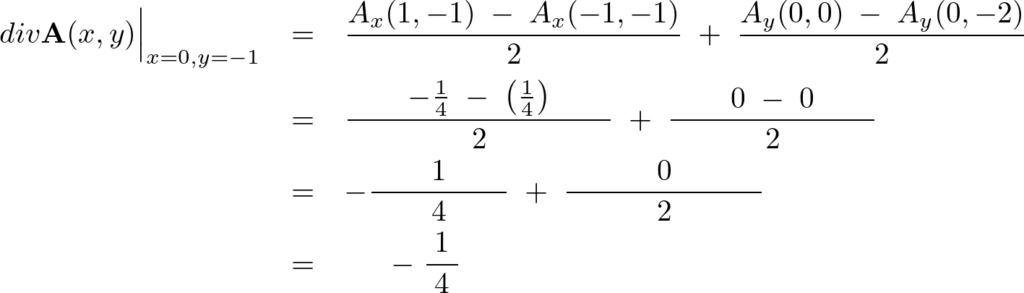
-
diff-eq.comスケールアップアップマイグレーション3
-
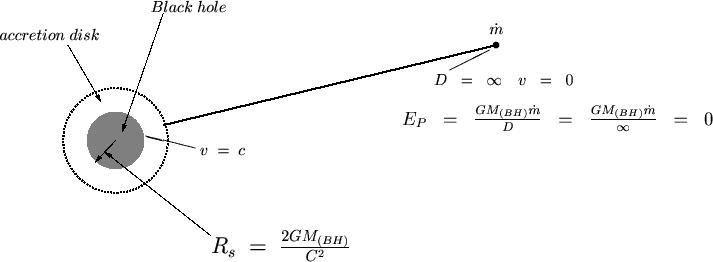
クェーサーとブラックホール
続きを読む
-
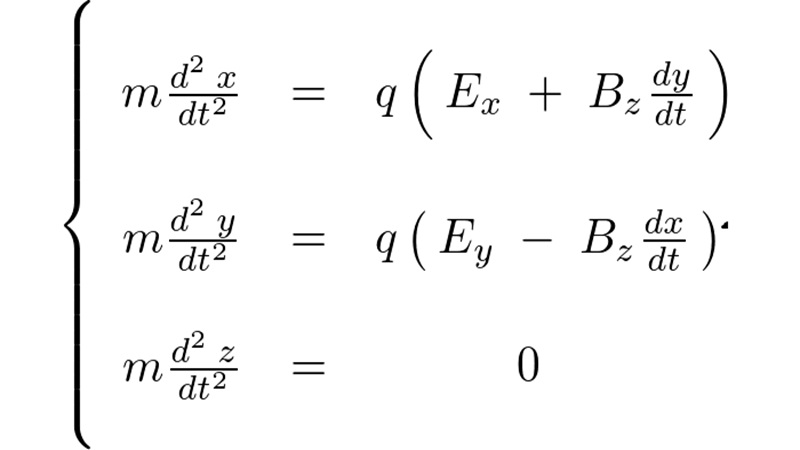
ベクトル解析 ━ 補遺
続きを読む
-
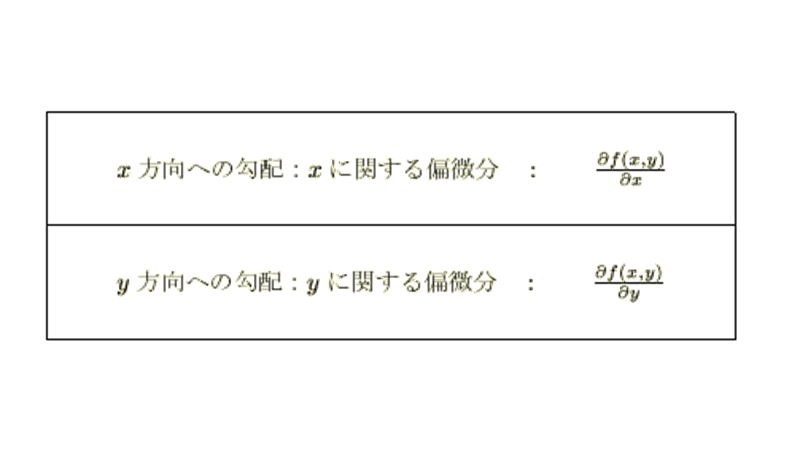
スカラー場、ベクトル場
続きを読む
-
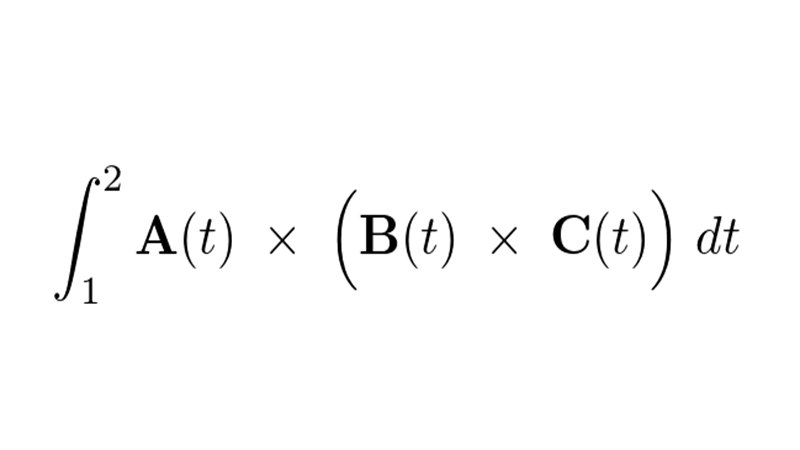
ベクトル積分問題の答え
続きを読む
-
-
Cisco Packet Tracer
カテゴリー : Cisco Packet TracerPacket Tracerとは、Ciscoが提供するCisco製のルータやスイッチなどをローカル端末上でコンフ…
-
-
-
-
-
-
-
-