行列式による連立方程式の解法
Cramerの公式
連立方程式というのは2次までを解くのは簡単ですが3次以上になるとそう簡単に解けるものではありません。
そこで考え出されたのが行列式を使ったクラメールの公式というものです。
今日に至ってはこの数学上の発見によって3次以上の連立方程式をシステマティックに解くことが可能になっています。
まずクラメールの公式というのを2次の式から見て行きましょう。
次に示すような連立方程式を考えます。
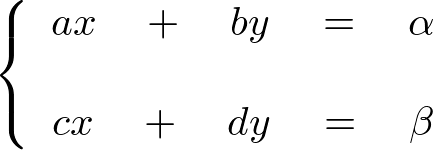
とすると、行列を使って、
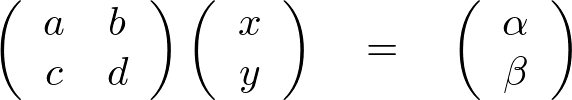
と表現できます。
そしてこのとき、
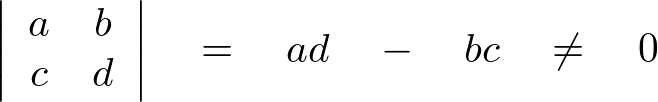
であるならば、解はつぎの式(Cramerの公式)で表されます。
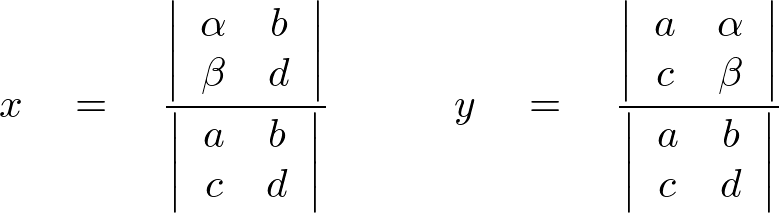
実際に2次の式で解いてみましょう。
例題
次に示すような連立方程式を先ほどの蔵メールの公式を使って解いていきましょう。
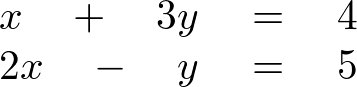
とすると、行列式を使った上記の連立方程式の表現は以下のようになります。
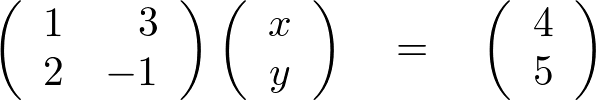
クラメールの公式を使うと次のようになります。
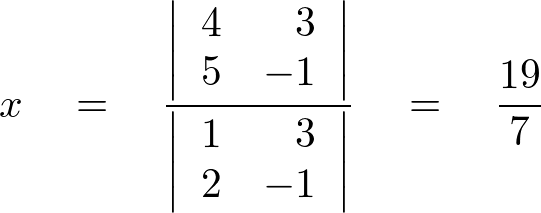
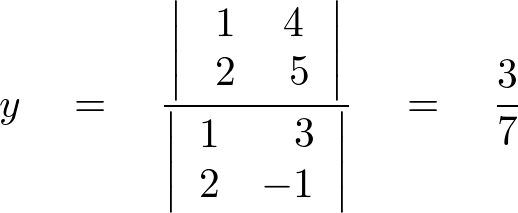
となります。
この公式が威力を発揮するのが3次以上になります。
次は実際に3次の連立方程式を解いてみましょう。
問題
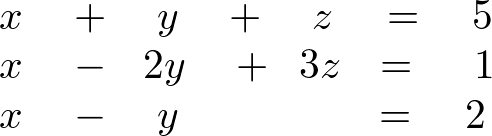
-
diff-eq.comスケールアップアップマイグレーション3
-
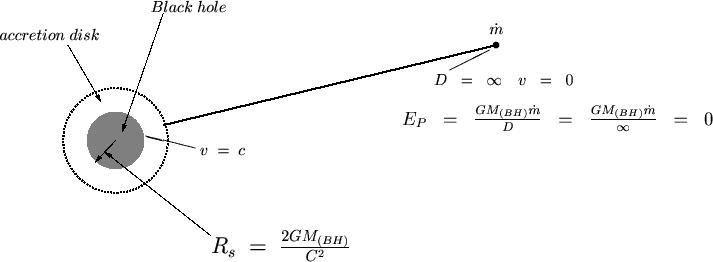
クェーサーとブラックホール
続きを読む
-
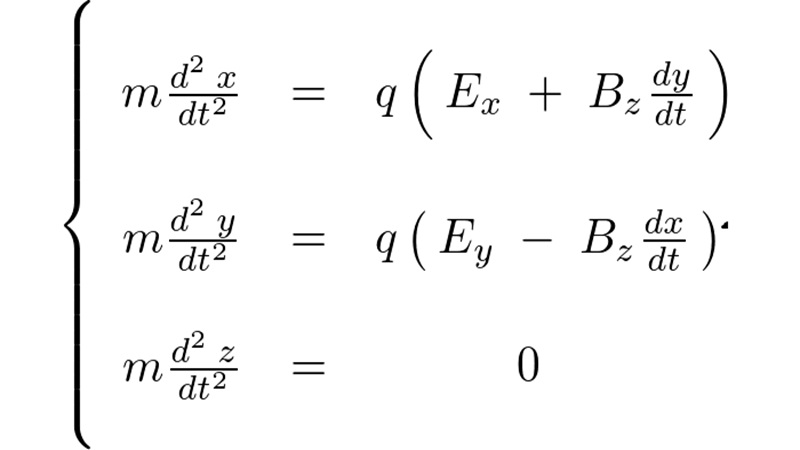
ベクトル解析 ━ 補遺
続きを読む
-
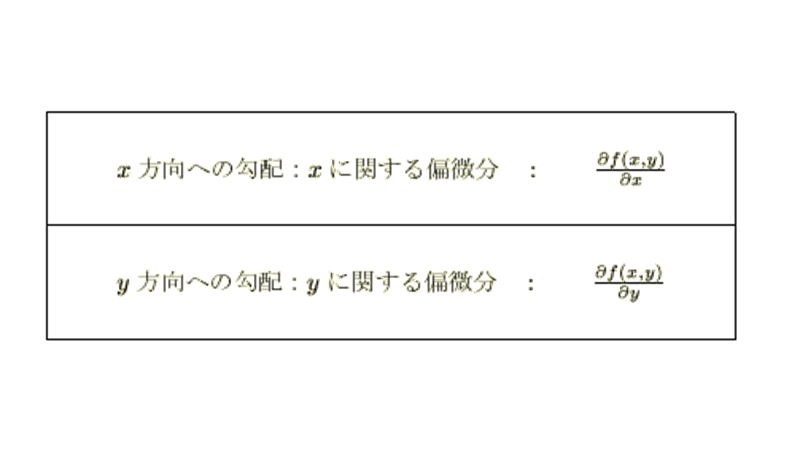
スカラー場、ベクトル場
続きを読む
-
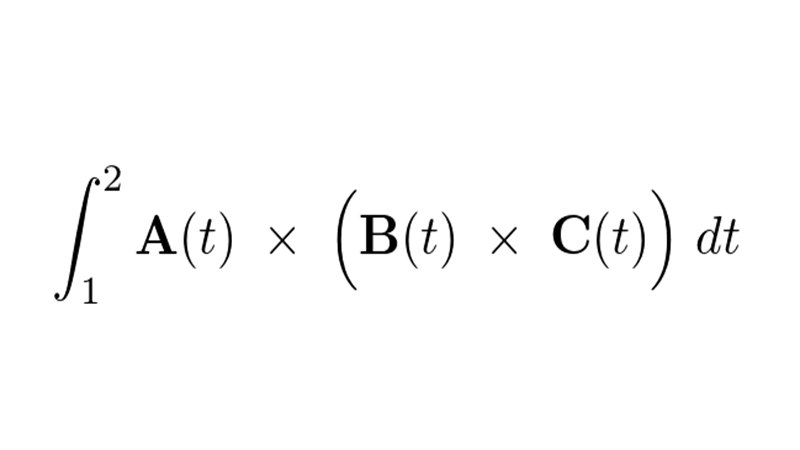
ベクトル積分問題の答え
続きを読む