逆行列
逆行列式の計算方法
3行3列以上の逆行列の計算方法
ここでは難しい定理や証明などは省いて計算方法と問題の解き方のみの説明をします。 まずは高校数学のおさらいをしてみましょう。
2行2列の逆行列式計算
高校で習う逆行列計算は2行2列まででした。
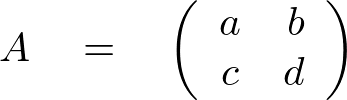
とすると、逆行列![]() は、
は、
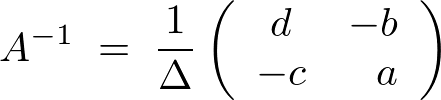
上記式の![]() は、
は、
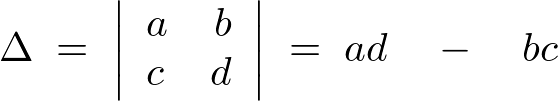
になります。
ここまではほとんどの方はご存知かと思います。 次に3行3列の逆行列を導きます。
だいぶ難しいんじゃないのかと思われるでしょうがそんなことはありません。
計算が少々面倒なだけであり、解法は実に単純です。 落ち着いてやってみましょう。
3行3列以上の逆行列の計算
3行3列以上の逆行列の公式は、
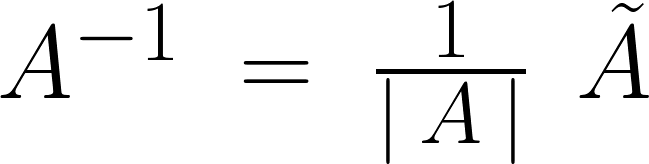
であり、ティルダ(Aの上にニョロっとしてるやつ)のマークがついているのは余因子とよばれるものです。分母のAはもちろん行列Aの行列式計算を施したものです。 この余因子というものはまず、小行列式というものを作り、さらにそれを転置したものになります。
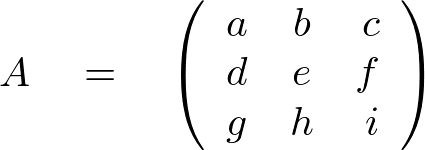
とすると、小行列式![]() は、
は、
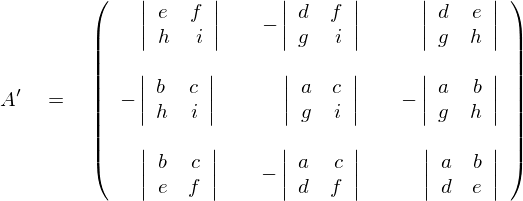
となります。
もとの行列Aの“a”の位置に対応する小行列式の中のものは、元のAのaのところから3時方向と6時方向にひいたライン上にない部分を抜き出したものです。それ以外のところのものも同じです。
例えば、もとの行列Aのfに関しては、そのfから12時方向と6時方向(上下方向)と9時方向にラインを引いたその線上にない部分を抜き出しているのがわかると思います。その抜き出した各々の行列式の集まりの行列が、いわゆる“小行列式”というものです。
ここで重要なのが符号ですが、これはプラスマイナスを交互にして番地のようにしてあると考えればよいでしょう。
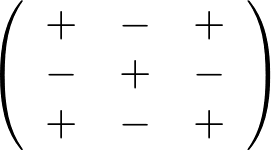
そしてこれを転置したものが、余因子と呼ばれるものになります。
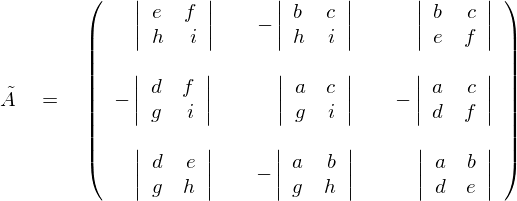
では早速、逆行列の計算をしてみましょう。 次の行列![]() の逆行列を計算してみましょう。
の逆行列を計算してみましょう。
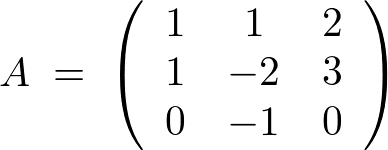
逆行列の計算問題の答えはこちら。
-
diff-eq.comスケールアップアップマイグレーション3
-
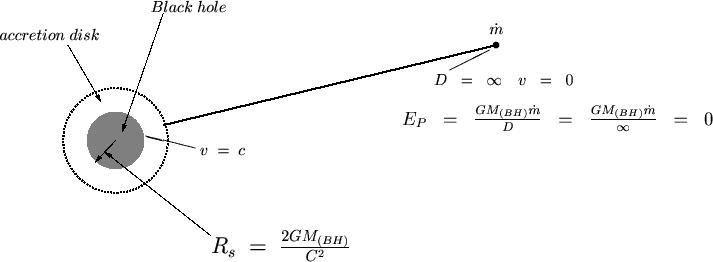
クェーサーとブラックホール
続きを読む
-
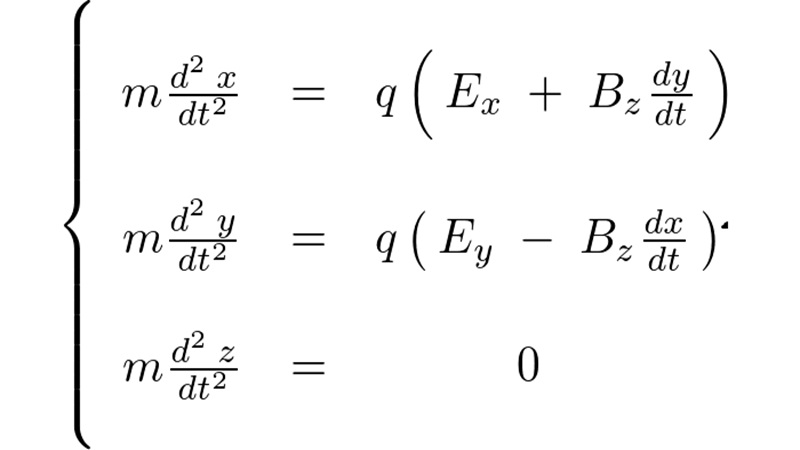
ベクトル解析 ━ 補遺
続きを読む
-
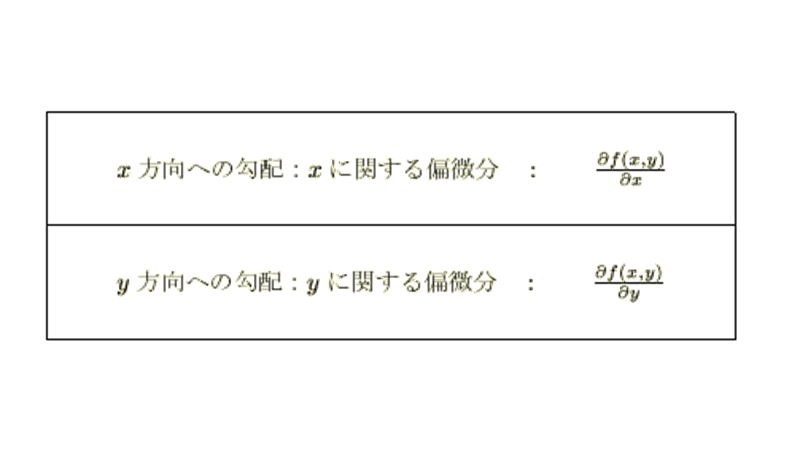
スカラー場、ベクトル場
続きを読む
-
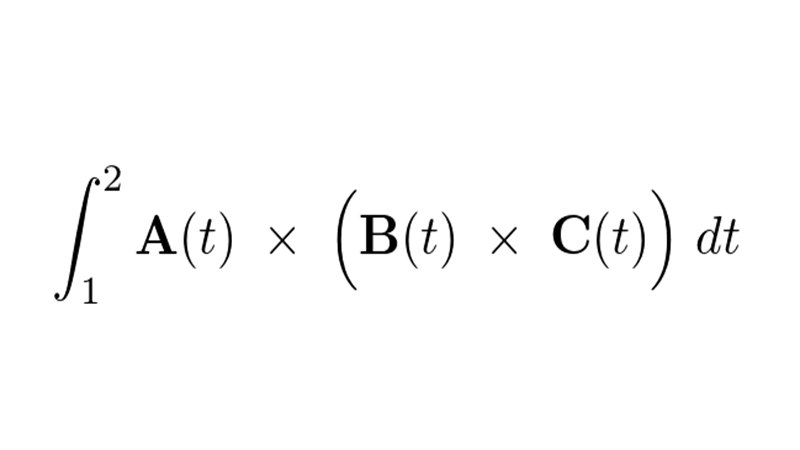
ベクトル積分問題の答え
続きを読む