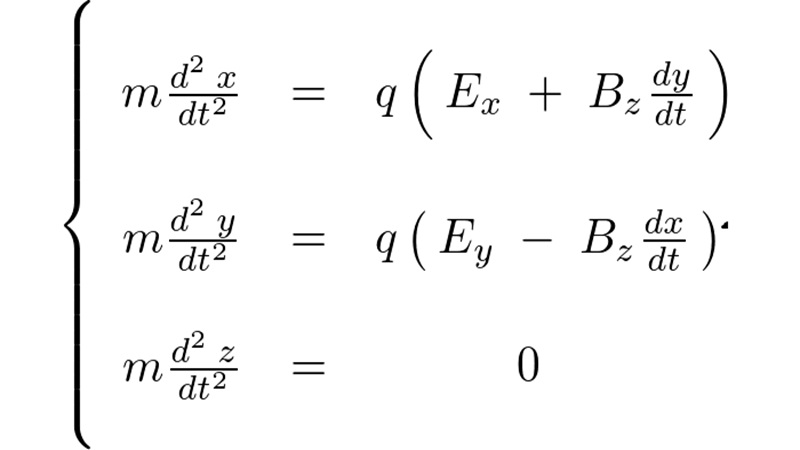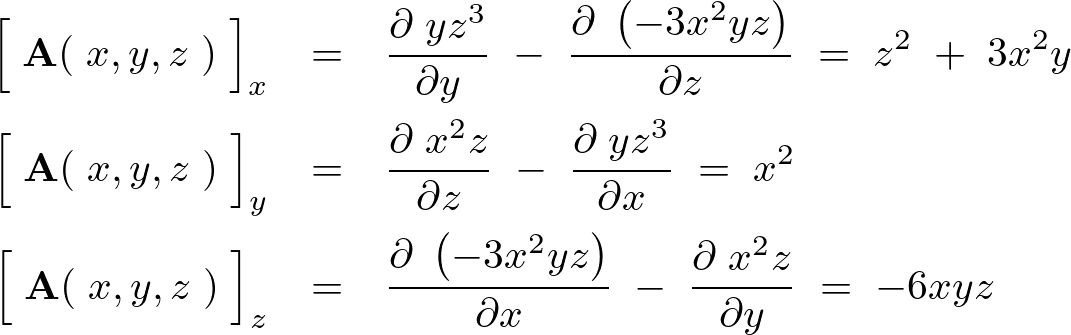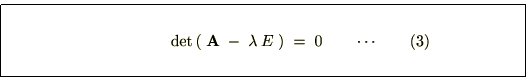対角化とは
対角化の方法とその意味
以下は2次元で考えます。
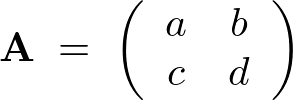
において、

を持っているとします。
つまり、
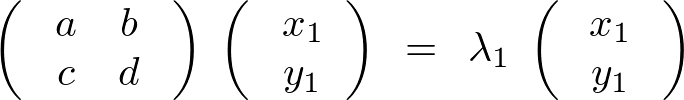
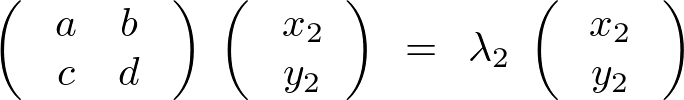
が成り立っているとします。これらを並べて書くと、
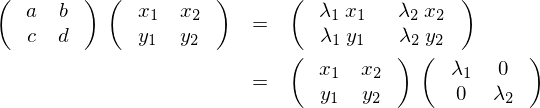
となります。
そしてこの式の両辺に右側から、
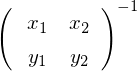
を掛けます。
すると、
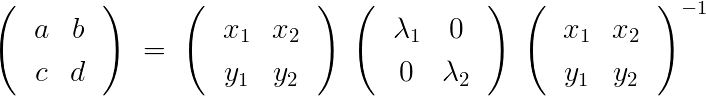
一般的に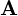 が
が![]() 行
行![]() 列の行列であるとき、
列の行列であるとき、
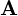 の固有値が
の固有値が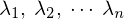
- 固有ベクトルが
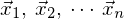
であるとし、
さらには対角化行列 を、
を、
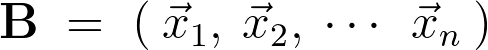
と定義すれば、
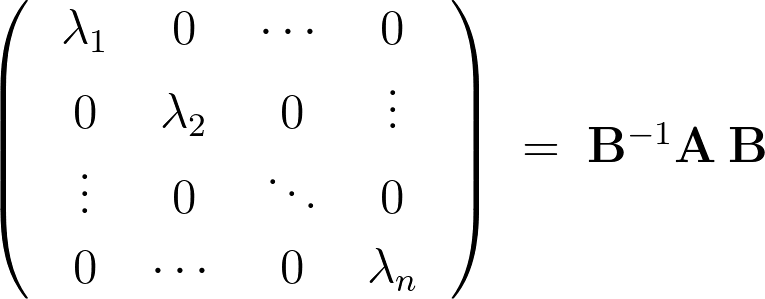
により、次のようなことが成り立ちます。
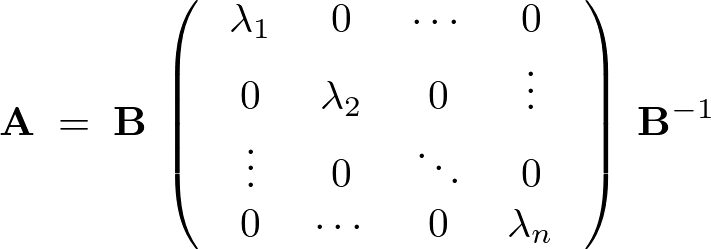
こういったのを用いれば、

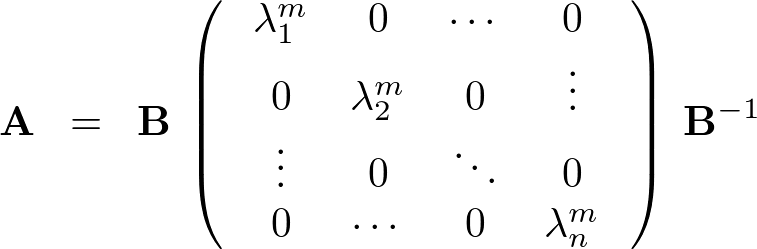
のようにすることが出来るので![]() 乗計算が計算できるようになります。
乗計算が計算できるようになります。
-
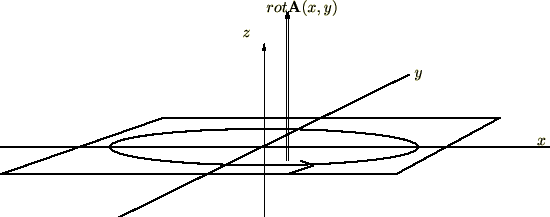
ベクトル場の回転 ━ ローテーション
続きを読む
-
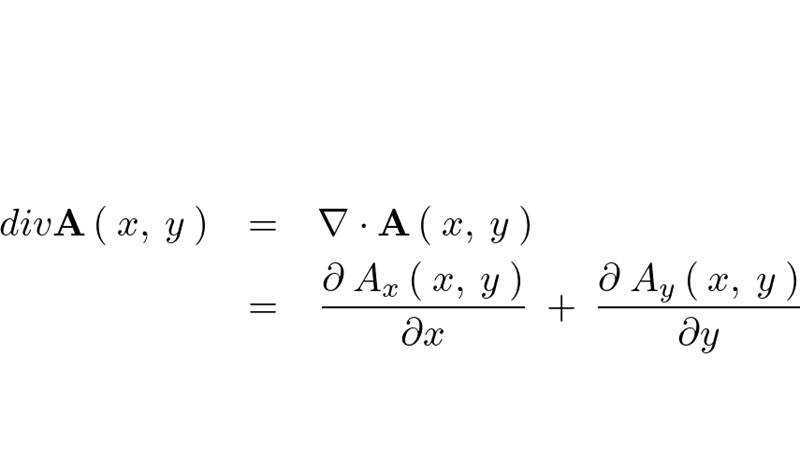
ベクトル場の発散の問題
続きを読む
-
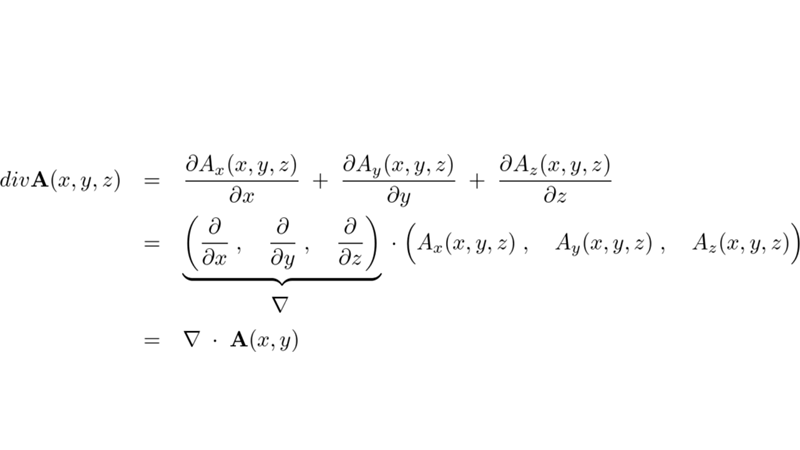
三次元ベクトル場および発散についての補足
続きを読む
-
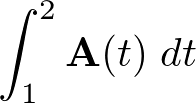
ベクトルの積分問題
続きを読む
-
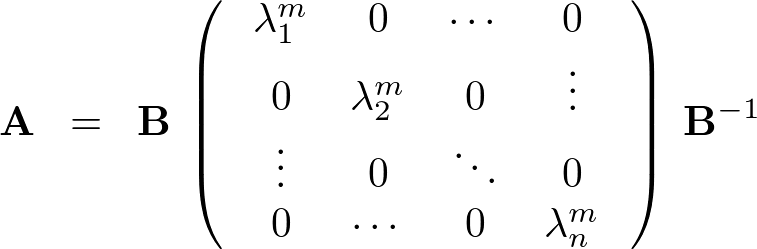
対角化
続きを読む
-
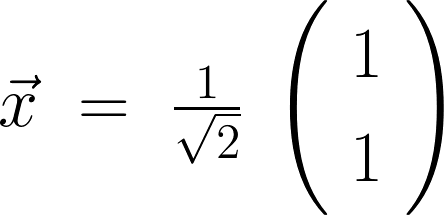
規格化
続きを読む
-
-
-
-
-
三次元ベクトル場および発散についての補足
カテゴリー : 三次元ベクトル場、発散についての補足三次元ベクトル場の発散(ダイバージェンス)に関して、ナブラとベクトル場の内積との関係について考察してみましょう…
-
-
-
-
-