ベクトル場の回転
ベクトル場の回転について(作成中)
ベクトル回転-ローテーション
ベクトル場の回転(ROT)
3次元方向の要素を持ったあるベクトル![]() を次のように考えます。
を次のように考えます。
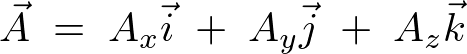
これに対し、次のようなベクトル場、
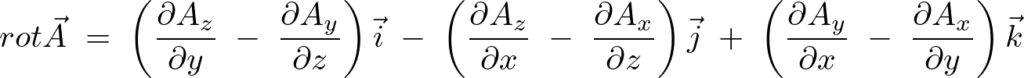
と表されるベクトル場を回転、またはローテーションといいます。
ナブラ
ここで作用素ナブラ
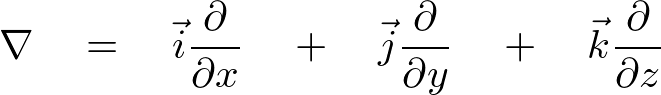
を導入すれば、
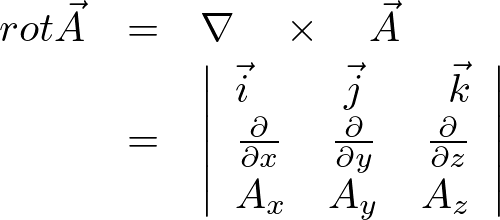
となります。
ここで先ほどの外積の計算で行ったときのように変形すると、この行列式で表された![]() は、
は、
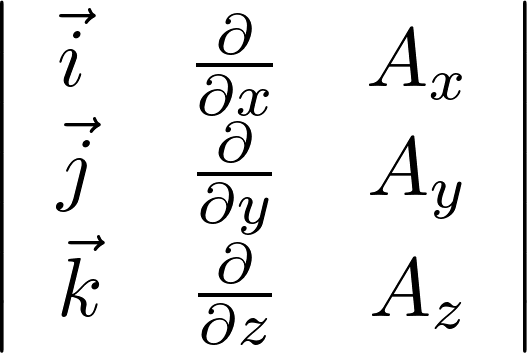
と表現できます。
この形だとあの長たらしい展開した状態の式を記憶する必要がないと思います。
次は実際にローテーションの計算を実行してみましょう。
【問題】
ベクトル![]() を次のように置きます。
を次のように置きます。
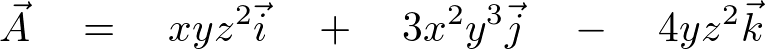
とします。
次に示すものを求めてみましょう。
問題①

問題②

答え
問題①
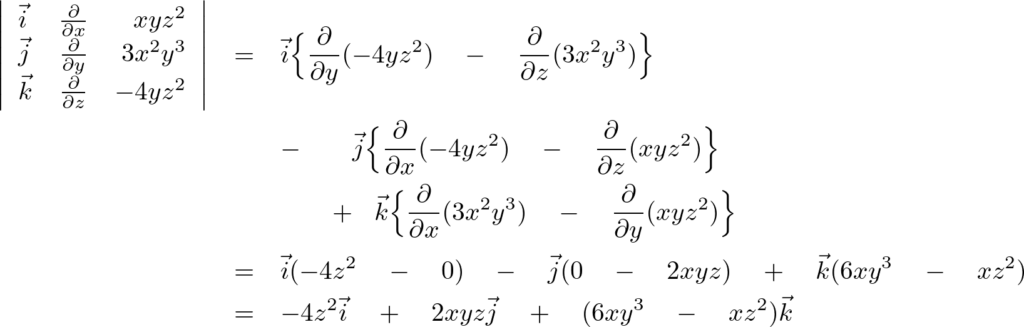
問題②
問題①の結果を利用します。
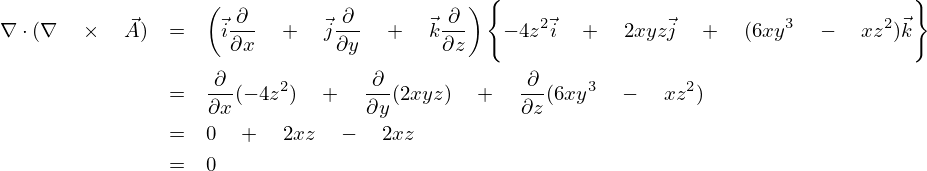
-
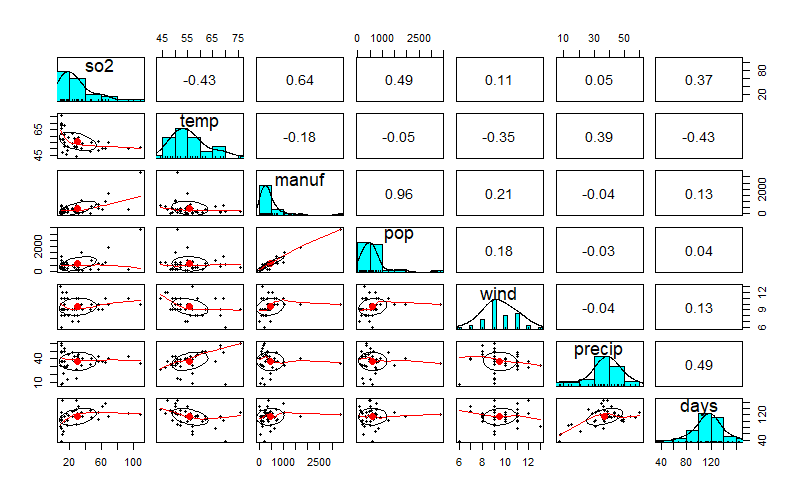
Rで重回帰分析-大気汚染①
続きを読む
-
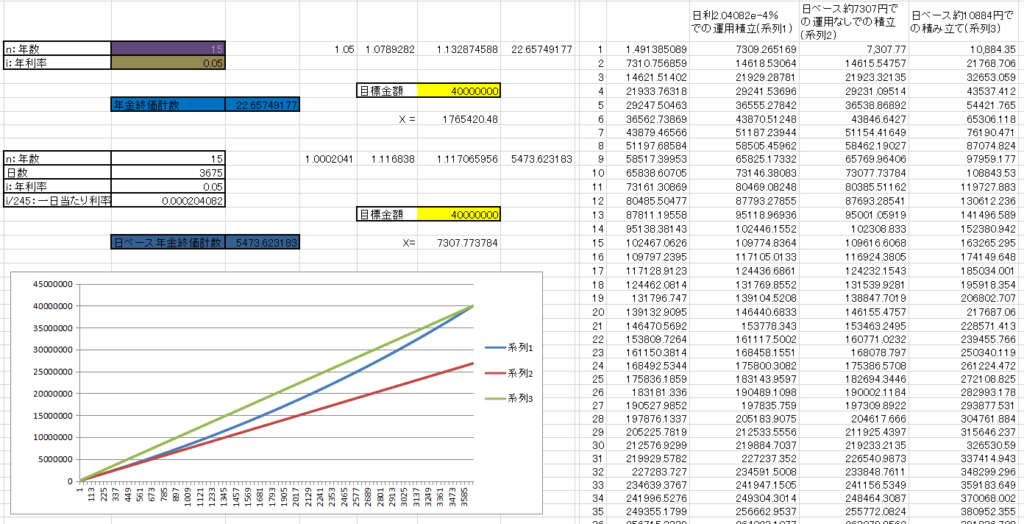
つみたてNISAと年金終価係数
続きを読む
-
diff-eq.comスケールアップアップマイグレーション4
-
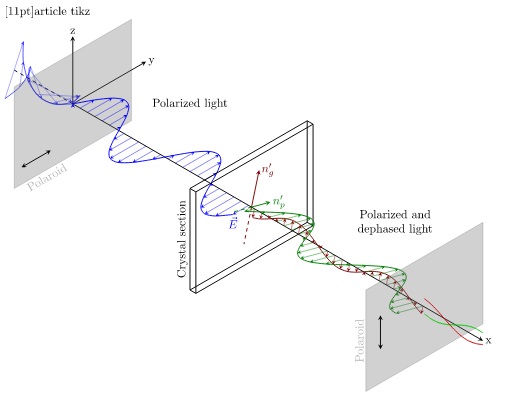
TikZ
続きを読む
-

年金終価係数
続きを読む
-
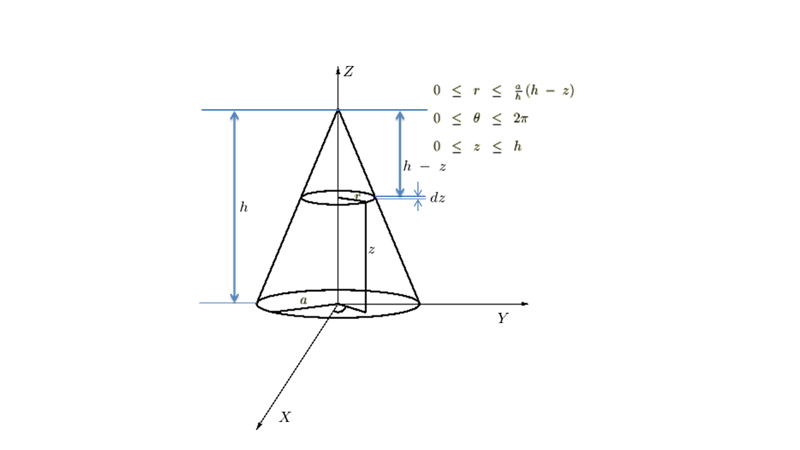
円錐の慣性モーメント
続きを読む
