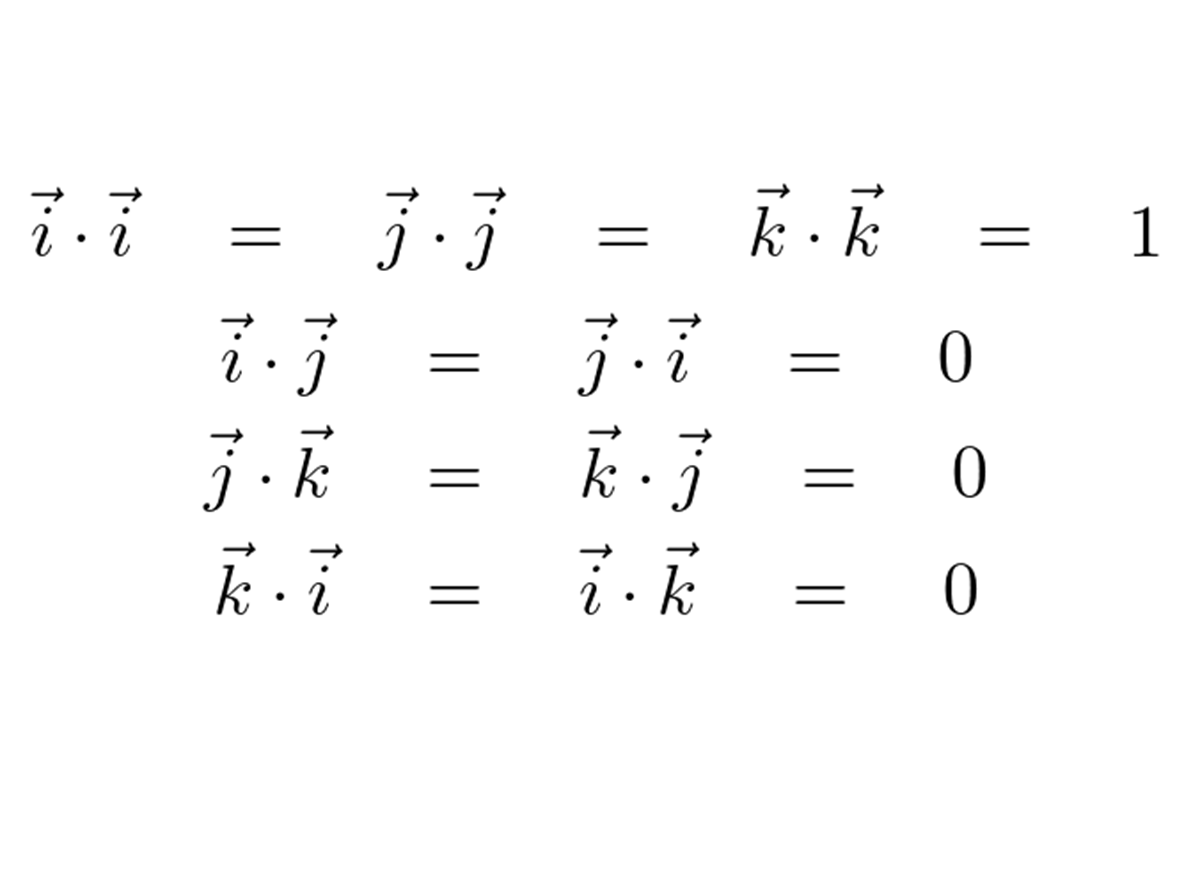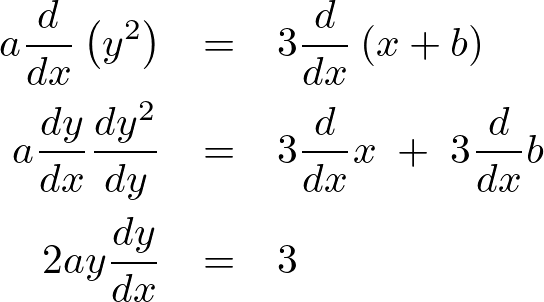線形代数 – 補遺
Dot Product
内積-Dot Product
2つのベクトル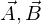 のつくる角度を
のつくる角度を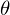 とするとき、
とするとき、

を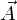 と
と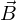 の内積と呼びます。
の内積と呼びます。
細かい説明はテキストに任せますが、基本ベクトル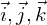 は次の公式が成り立ちます。
は次の公式が成り立ちます。
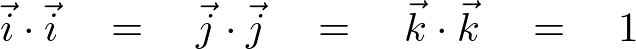
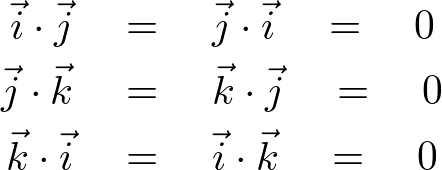
rotationのセクションの問題ではこの公式が使われています。
ちなみに外積をCross Productと言ってますが、内積のほうはDot Productとよんだりします。
偏微分
rotationの計算で出てきました∂という記号がありました。
これは偏微分せよという記号でラウンドなどと呼ばれたりしています。
特に難しく考えることはなくただ単に分母にある変数で微分せよ、という意味です。
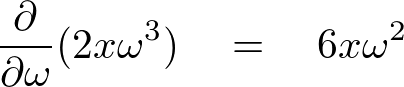
とこんな具合です。
転置行列-transposed matrix
特に難しく考えるまでもなく行列要素の行と列を(左上から右下に走る対角線上に)入れ換えた(ひっくり返した)だけです。
例えば4行4列の行列、
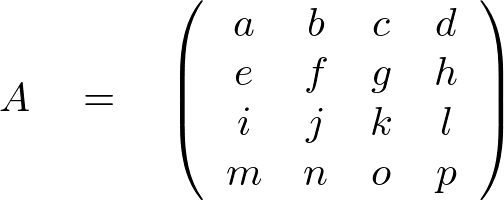
は、転置すると、
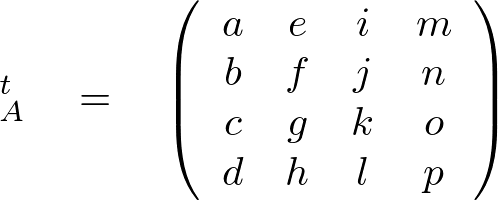
となります。

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
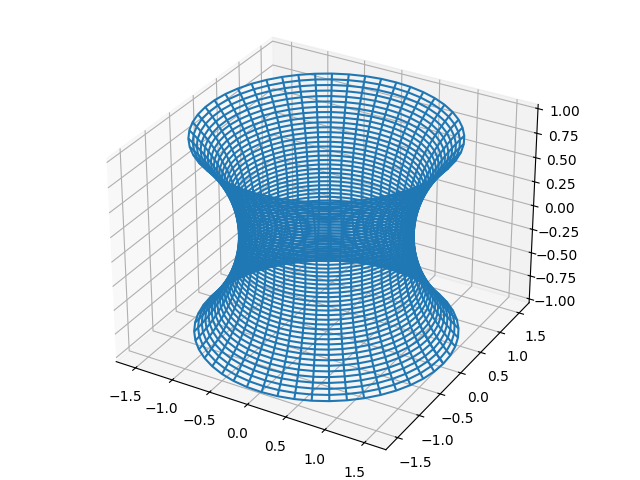
Pythonによるラプラス方程式の描画
サテライトサイト「微分方程式いろいろ」コンテンツ内で取り上げた「ラプラス方程式」にて使用されたPythonグラフィックスになります。
ラプラス方程式とは、2階の線型楕円型偏微分方程式のことになります。領域内においてある境界条件を満たすラプラス方程式を求め、それによりさまざまな解析解を導くことが可能です。
ここでは簡単な例として長方形プレートの平衡温度分布に関して、2次元のラプラス方程式で導き出した解をPythonの3次元描画によって表現します。
ラプラス演算子
ひとまずラプラス方程式に関しての簡単な予備知識を考察していきます。
それぞれの座標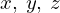 とした3次元座標空間において2階の偏微分作用素を
とした3次元座標空間において2階の偏微分作用素を とし、この作用素を次のようにおきます。
とし、この作用素を次のようにおきます。
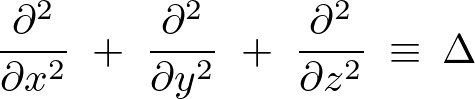
-
微分方程式いろいろTOPページLaTeXコード
カテゴリー : 微分方程式いろいろLaTeXコードサテライトサイト微分方程式いろいろコンテンツトップページに使われたコードになります。コンパイル時のエラー等の修…
-
-
Cisco Packet Tracer
カテゴリー : Cisco Packet TracerPacket Tracerとは、Ciscoが提供するCisco製のルータやスイッチなどをローカル端末上でコンフ…
-
-
-
-
-
-
-