���m�点
��Web�T�C�g�̓T�C�g�쐬�V�X�e���̐[���Ȍ��ׂɂ�茻�݃����N�̕ύX���s���Ă���܂��B�Ǘ��l�����Z�̂��߃��_�C���N�g�T�C�g�͍쐬�����A���ڃ����N�ύX���s���\��ł��B�������������������B�����͖���ɂȂ�܂��B
�����̃y�[�W�͂Ȃ�ׂ��c���悤�ɂ��܂������ŕύX���܂��̂Ńu�b�N�}�[�N�Ȃǂ��Ă�����́A���ʓ|�ɂȂ邩�Ǝv���܂������̃h���C��https://mathematical.jp/mathematical/�@����ړI�̃y�[�W�ɍs���悤�ɂ��肢�\���グ�܂��B
�ʎq�͊w�I�Ȓ��a�U���q�̍l�@
�͊w�ɂ����ė��z�I�ȃo�l�ɂȂ��ꂽ���̂̐U������l�q�����������̂���ʓI�ɒ��a�U���q�Ȃǂƌ������肵�܂����A����̓V�����[�f�B���K�[�������ɓ��Ă͂߂Ă������ꍇ�A�����I�ɂǂ̂悤�ȐU�������������l�@���Ă����܂��B
�����ňꎟ�����a�U���q�ɂ�����|�e���V�����u�����̂悤�ɒu���܂��B
�O��o�Ă����V�����[�f�B���K�[�������ƌĂ����͎̂��Ɏ����悤�Ȃ��̂ł����B
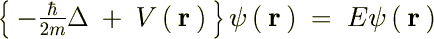
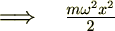
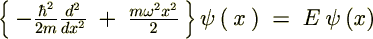
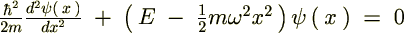
���W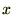 �̑����
�̑����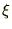 ���g���ĕϐ��ϊ���
���g���ĕϐ��ϊ���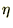 ��p����
��p����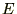 �����̂悤�ɒu���܂��B
�����̂悤�ɒu���܂��B
��p�f���`�F�[��������p�f���̂��̂�ω������܂��B
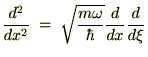
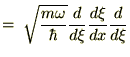
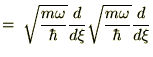
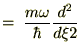
2�K�̍�p�f�͎��̂悤�ɕό`�ł��܂��B
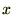 �̑����
�̑����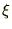 ���g���ĕϐ��ϊ���
���g���ĕϐ��ϊ���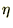 ��p����
��p����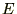 �����̂悤�ɒu���܂��B
�����̂悤�ɒu���܂��B
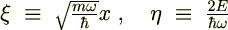
��p�f���`�F�[��������p�f���̂��̂�ω������܂��B
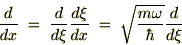
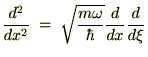
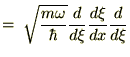
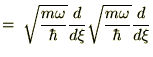
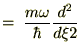
2�K�̍�p�f�͎��̂悤�ɕό`�ł��܂��B
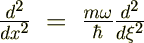
���̌��ʂ��g���Đ�̃V�����[�f�B���K�[��������ό`���Ă����܂��B
������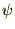 �����̂悤�ɂ����āA
�����̂悤�ɂ����āA
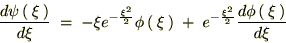
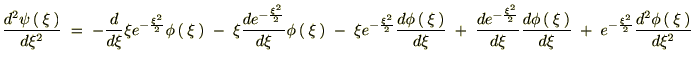
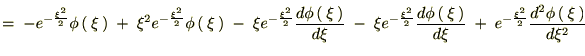
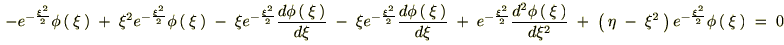
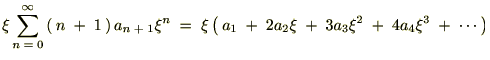
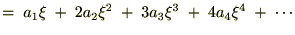
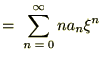
������Ă܂Ƃ߂āc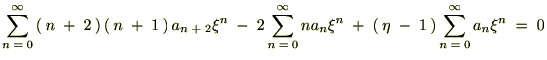
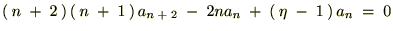
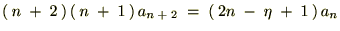
��������Ǝ��̂悤�ȊW����������܂��B
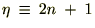 �Ƃ���������t�����
�Ƃ���������t�����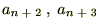 �̓[���ɂȂ���
�̓[���ɂȂ���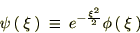 �͎������܂��B
�͎������܂��B
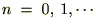 �ɂ����
�ɂ����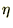 �����肳��邱�ƂɂȂ�܂����A���ꂪ���U���Ȃ��悤�ɂ���悭�A
�����肳��邱�ƂɂȂ�܂����A���ꂪ���U���Ȃ��悤�ɂ���悭�A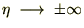 ��
��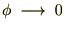 �ƂȂ邽�߂�
�ƂȂ邽�߂�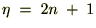
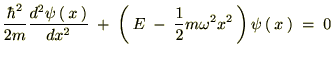
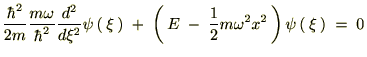
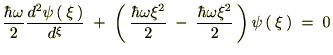
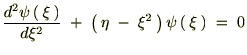
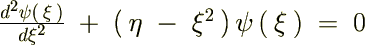
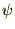 �����̂悤�ɂ����āA
�����̂悤�ɂ����āA
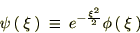
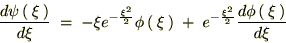
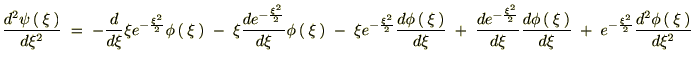
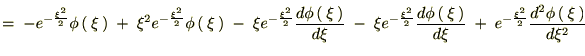
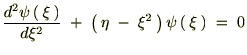
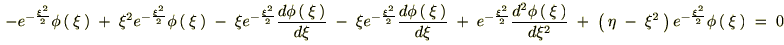
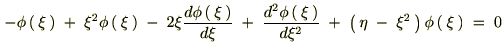
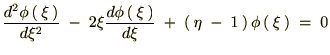
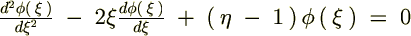
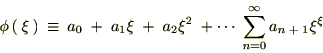
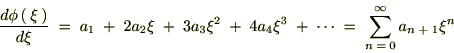
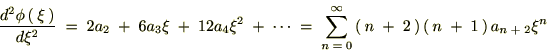
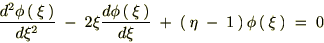
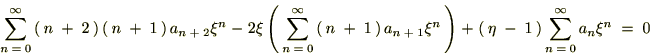
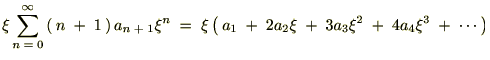
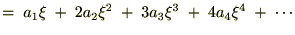
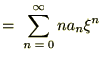
������Ă܂Ƃ߂āc
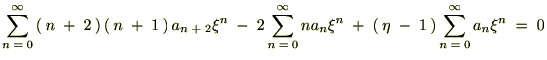
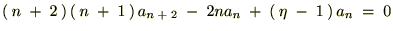
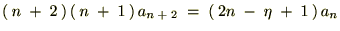
��������Ǝ��̂悤�ȊW����������܂��B
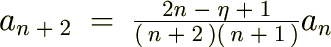
�����̌��ʂ̈Ӗ��͕��q��
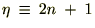 �Ƃ���������t�����
�Ƃ���������t�����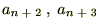 �̓[���ɂȂ���
�̓[���ɂȂ���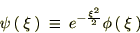 �͎������܂��B
�͎������܂��B
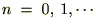 �ɂ����
�ɂ����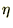 �����肳��邱�ƂɂȂ�܂����A���ꂪ���U���Ȃ��悤�ɂ���悭�A
�����肳��邱�ƂɂȂ�܂����A���ꂪ���U���Ȃ��悤�ɂ���悭�A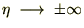 ��
��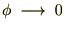 �ƂȂ邽�߂�
�ƂȂ邽�߂�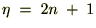

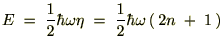
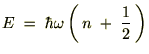
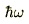 ���Ƃ̋ϓ��ȃ��x���ŕ\����邱�ƂɂȂ�܂��B
���Ƃ̋ϓ��ȃ��x���ŕ\����邱�ƂɂȂ�܂��B