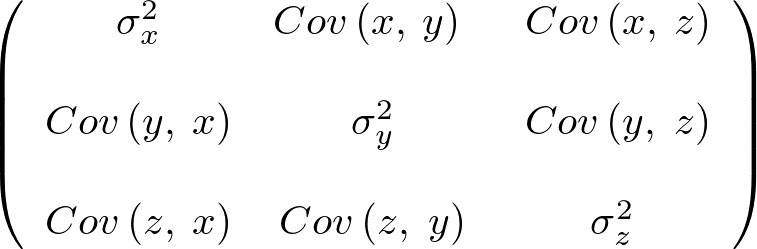データの表現
平均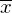 の表し方
の表し方

これより、

中央値(median):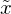

標本分散(variance):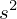
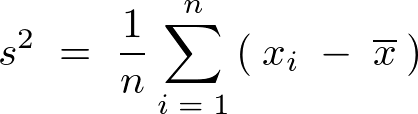
上記標本分散の平方根が標本標準偏差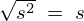 になる。
になる。
![]() で割るかわりに
で割るかわりに![]() で割った次のようなもの、
で割った次のようなもの、
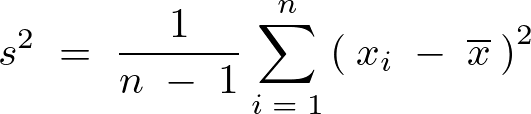
を不偏分散という。
分散式の計算
分散を英語のVarianceから![]() と表し、平均
と表し、平均![]() を用いて確率変数
を用いて確率変数![]() の分散
の分散![]() を次のように表現する。
を次のように表現する。
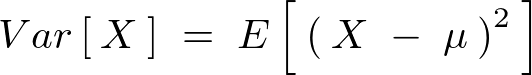
これを計算していくと、
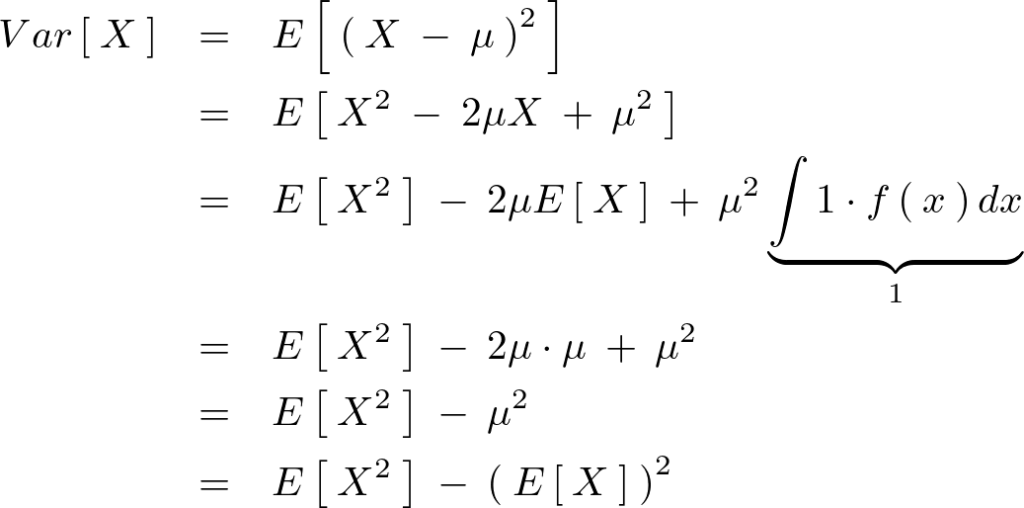
より、

共分散
![]() と
と![]() の
の![]() 組のデータの分散の積を
組のデータの分散の積を![]() 倍したものを共分散として
倍したものを共分散として![]() と置いて次のように表現する。
と置いて次のように表現する。
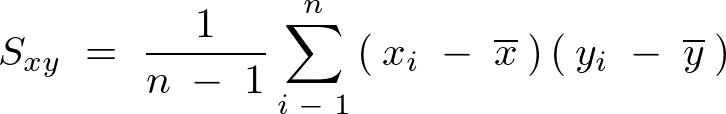
確率変数![]() と
と![]() の期待値を次のようにおく。
の期待値を次のようにおく。
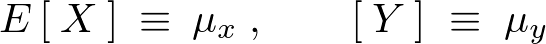
確率変数![]() と
と![]() の共分散は、
の共分散は、
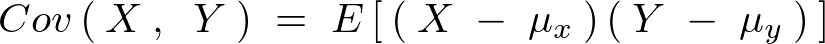
上記式右辺を計算していけば、
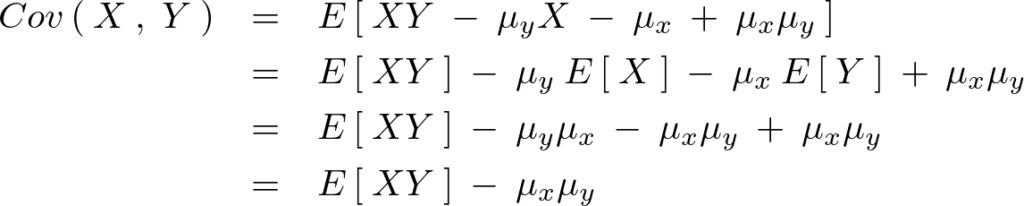

または、
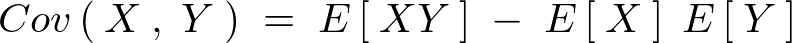
コンテンツ紹介
分散共分散行列
分散共分散行列とは何なのかを数理的に詳しく考察していきます。
多変量確立ベクトルの計算
多変量確立ベクトルに関しての基本的な内容とその証明などを取り扱います。


 の式を計算していきます。
の式を計算していきます。