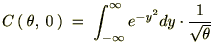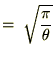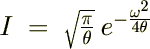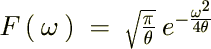���m�点
��Web�T�C�g�̓T�C�g�쐬�V�X�e���̐[���Ȍ��ׂɂ�茻�݃����N�̕ύX���s���Ă���܂��B�Ǘ��l�����Z�̂��߃��_�C���N�g�T�C�g�͍쐬�����A���ڃ����N�ύX���s���\��ł��B�������������������B�����͖���ɂȂ�܂��B
�����̃y�[�W�͂Ȃ�ׂ��c���悤�ɂ��܂������ŕύX���܂��̂Ńu�b�N�}�[�N�Ȃǂ��Ă�����́A���ʓ|�ɂȂ邩�Ǝv���܂������̃h���C��https://mathematical.jp/mathematical/�@����ړI�̃y�[�W�ɍs���悤�ɂ��肢�\���グ�܂��B
�t�[���G�ϊ�
���镡�G�Ȋ��ɂ����āA�Ⴆ��A�̐��E�̌��ۂ�B�̐��E�̊��ɕϊ����Ă����Ă��������ʂ����悭����Ƃ������A������������Ȋ����̐��w�I�_�@�Ƀt�[���G�ϊ��ƌĂ����̂�����܂��B
��ʓI�ɂ��̌`�͐ϕ��̌`�ŕ\����A�͈͂�
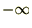 ����
����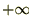 �̐ϕ��̈�̌`�ŕ\������܂��B
�̐ϕ��̈�̌`�ŕ\������܂��B
��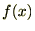 ���l��
���l��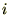 �������P�ʂƂ����
�������P�ʂƂ����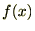 �̃t�[���G�ϕ��\�����A
���ɂ���
�̃t�[���G�ϕ��\�����A
���ɂ���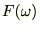 ��
��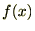 �̃t�[���G�ϊ��Ƃ���ƁA
�̃t�[���G�ϊ��Ƃ���ƁA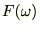 �́A
�����Ŏ��Ɏ������悤�Ȃ�������l���܂��B
�́A
�����Ŏ��Ɏ������悤�Ȃ�������l���܂��B
���̎��Ƀt�[���G�ϊ���K�p���Ă����ƁA
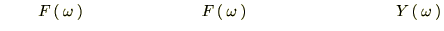
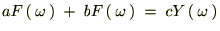
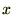 �̐��E�̌��ۂ�
�̐��E�̌��ۂ�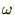 �̐��E�̌��ۂɒu��������Ă��܂��B��������ƍ��܂�
�̐��E�̌��ۂɒu��������Ă��܂��B��������ƍ��܂�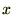 �̐��E�Ō��Ă����ꍇ�킩�肸�炩�������̂��A
�̐��E�Ō��Ă����ꍇ�킩�肸�炩�������̂��A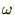 �ɒu������邱�ƂŌ��ʂ������邭�Ȃ�A���̌��ۂ��킩��₷���Ȃ�Ƃ������_������܂��B
�ɒu������邱�ƂŌ��ʂ������邭�Ȃ�A���̌��ۂ��킩��₷���Ȃ�Ƃ������_������܂��B
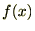 ���l��
���l��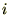 �������P�ʂƂ����
�������P�ʂƂ����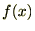 �̃t�[���G�ϕ��\�����A
�̃t�[���G�ϕ��\�����A
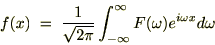
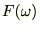 ��
��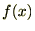 �̃t�[���G�ϊ��Ƃ���ƁA
�̃t�[���G�ϊ��Ƃ���ƁA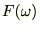 �́A
�́A
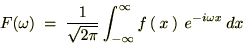
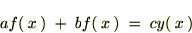
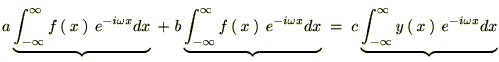
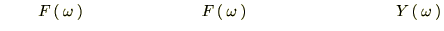
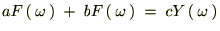
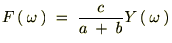
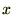 �̐��E�̌��ۂ�
�̐��E�̌��ۂ�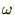 �̐��E�̌��ۂɒu��������Ă��܂��B��������ƍ��܂�
�̐��E�̌��ۂɒu��������Ă��܂��B��������ƍ��܂�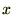 �̐��E�Ō��Ă����ꍇ�킩�肸�炩�������̂��A
�̐��E�Ō��Ă����ꍇ�킩�肸�炩�������̂��A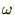 �ɒu������邱�ƂŌ��ʂ������邭�Ȃ�A���̌��ۂ��킩��₷���Ȃ�Ƃ������_������܂��B
�ɒu������邱�ƂŌ��ʂ������邭�Ȃ�A���̌��ۂ��킩��₷���Ȃ�Ƃ������_������܂��B
���̑��̐���
�܂�����ɂ͎w������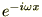 �ɂ͎��Ɏ����悤��
�ɂ͎��Ɏ����悤��
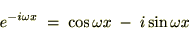
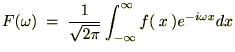
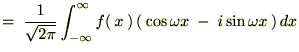
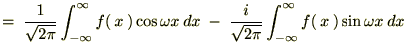
���̏�L���ɂ�����
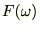 ���������ł���ΉE�ӑ�2���͂O�A����ł���ΉE�ӑ�1���̂ق����O�ɂȂ�Ƃ�������������܂��B
���������ł���ΉE�ӑ�2���͂O�A����ł���ΉE�ӑ�1���̂ق����O�ɂȂ�Ƃ�������������܂��B���̐����́A��ɏo�Ă���K�E�X���̃t�[���G�ϊ��v�Z���ɂ����ė��p���܂��̂łƂ肠���������������̂ȂȂƂ��������Ŋo���Ă����Ă��������B
�K�E�X�ϕ��̊T�v
������Ԃɂ�����ϕ��ő��ɃK�E�X�ϕ��ƌĂ����̂�����܂��B
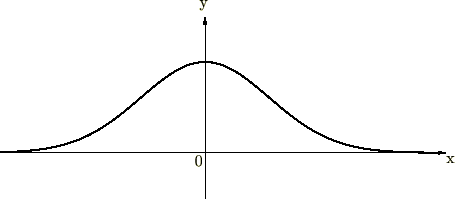
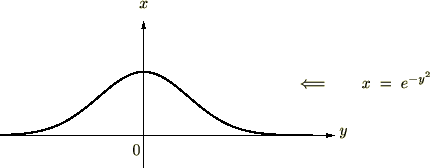
���̐}�͎w����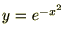 ��`�悵�����̂ł��B
��`�悵�����̂ł��B
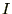 �ƒu���܂��B����
�ƒu���܂��B����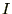 ��2�悵�����̂ɑ��ċɍ��W��K�p������ƁA
��2�悵�����̂ɑ��ċɍ��W��K�p������ƁA
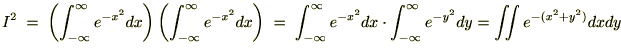
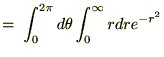
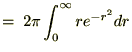
������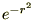 ��
��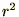 ��
��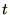 �ƒu���āA
�ƒu���āA
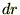 �̕ϊ��i�u���j�����ĕϐ��ϊ��B
�̕ϊ��i�u���j�����ĕϐ��ϊ��B
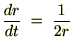
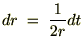
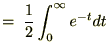
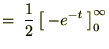
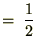
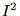 �́A
�́A
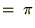
���̐}�͎w����
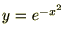 ��`�悵�����̂ł��B
��`�悵�����̂ł��B
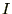 �ƒu���܂��B����
�ƒu���܂��B����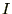 ��2�悵�����̂ɑ��ċɍ��W��K�p������ƁA
��2�悵�����̂ɑ��ċɍ��W��K�p������ƁA
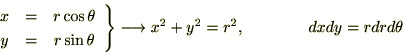
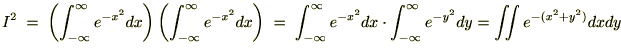
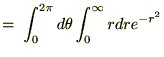
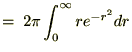
������
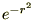 ��
��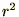 ��
��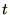 �ƒu���āA
�ƒu���āA
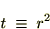
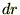 �̕ϊ��i�u���j�����ĕϐ��ϊ��B
�̕ϊ��i�u���j�����ĕϐ��ϊ��B
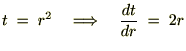
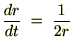
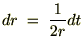

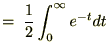
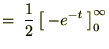
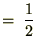
���̌��ʂɂ����
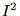 �́A
�́A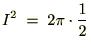
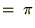
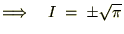
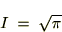
�K�E�X�ϕ��̃t�[���G�ϊ�
���̂悤�ȃK�E�X���Ɋւ��ăt�[���G�ϊ�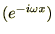 �����Ă������ꍇ�ǂ̂悤�ȕ������������邩���l�@���Ă����܂��B
�����Ă������ꍇ�ǂ̂悤�ȕ������������邩���l�@���Ă����܂��B
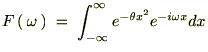
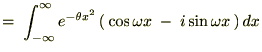
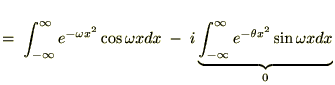
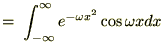
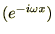 �����Ă������ꍇ�ǂ̂悤�ȕ������������邩���l�@���Ă����܂��B
�����Ă������ꍇ�ǂ̂悤�ȕ������������邩���l�@���Ă����܂��B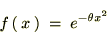
�t�[���G�ϊ����́A
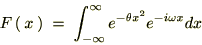
�����Ŏ��̐���
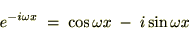
����������Čv�Z���Ă����܂��B
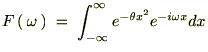
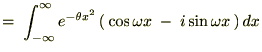
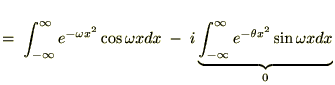
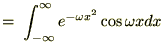
�����ŏo�Ă����ϕ��������̂悤�ɒu���܂��B
����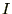 ���ɑ��Ď��̂悤��
���ɑ��Ď��̂悤��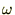 �Ɋւ��Ă̕Δ������s���Ă݂܂��傤�B
�Ɋւ��Ă̕Δ������s���Ă݂܂��傤�B
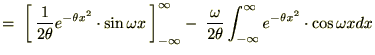
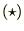 ���A
���A
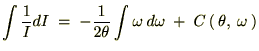
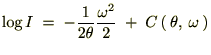
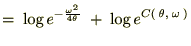
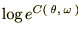 ��������
��������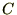 �ƒu���A����ɒ萔
�ƒu���A����ɒ萔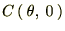 �����߂Ă����܂��B
�����߂Ă����܂��B
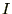 �����ɖ߂��ƁA
�����ɖ߂��ƁA
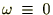 �Ƃ���ƁA
�Ƃ���ƁA
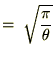

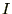 ���ɑ��Ď��̂悤��
���ɑ��Ď��̂悤��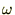 �Ɋւ��Ă̕Δ������s���Ă݂܂��傤�B
�Ɋւ��Ă̕Δ������s���Ă݂܂��傤�B
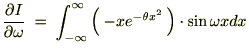
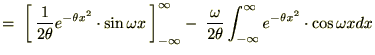
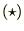 ���A
���A
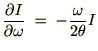
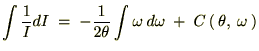
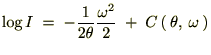
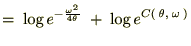
�o�Ă����㎮��
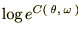 ��������
��������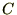 �ƒu���A����ɒ萔
�ƒu���A����ɒ萔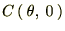 �����߂Ă����܂��B
�����߂Ă����܂��B
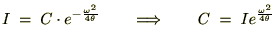
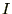 �����ɖ߂��ƁA
�����ɖ߂��ƁA
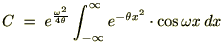
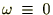 �Ƃ���ƁA
�Ƃ���ƁA
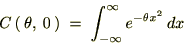
�K�E�X�ϕ����o�Ă���̂ł�����قǂ̂����œ����悤�Ɍv�Z���Ă����܂��B
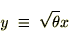

������Ă����܂��B