ベクトル内積外積の数学的一般化

ベクトルの成分計算

ベクトルのそれぞれの成分を、単位ベクターを使い、

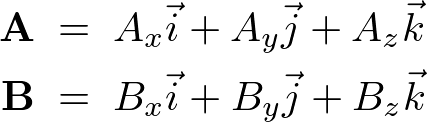
と書くとき、その内積の成分計算は次のようになります。

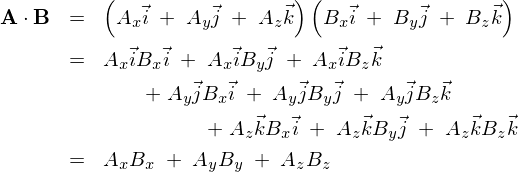
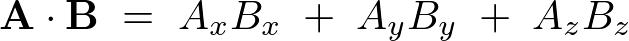
外積の数学的一般化

ここで

と書いた場合、

これは、

• 大きさ　
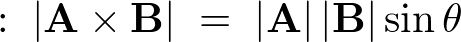
• 向き　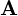　と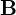に垂直で、かつ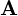から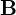へ回した右ねじの進む方向であるような「ベクトル」

を表します。

そしてこのをとの外積といいます。

また、分配法則として次のようなことが成り立ちます。

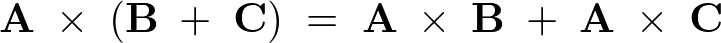
同じベクトルどうしの外積はになります。

理由はの大きさは定義により、

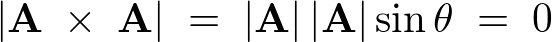
であるので、同じ大きさのベクトルはになります。

しかしここで注意すると、外積はベクトル積であるので、

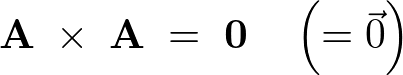
という表記が正しいです。

わかりずらいかもしれませんが右辺は零ベクトルです。

今度は具体的にベクトルの中身の計算をやってみましょう。

外積の計算

まず計算するベクトルを、

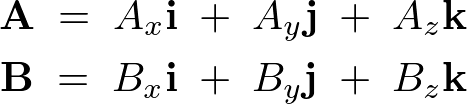
とします。

このときの外積次のように計算されます。

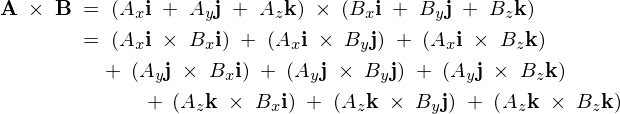
異なる単位ベクトルの外積を考えます。

まず、異なる単位ベクトル間の外積の大きさは、

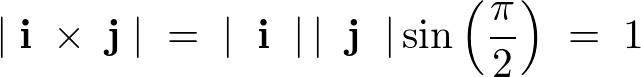
同様にして、

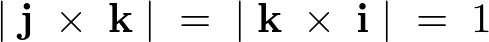
となります。

では異なる単位ベクトルの外積の向きはどうなるでしょうか。

まず、を考えます。

の向きは外積の定義によりとに垂直で、とに回した右ねじの進む向きだからこれは結局のところの向きです。

先の結果からだったので結局のところ、

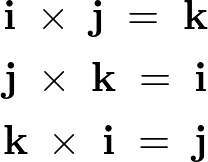
また、外積の順序を逆にすると、

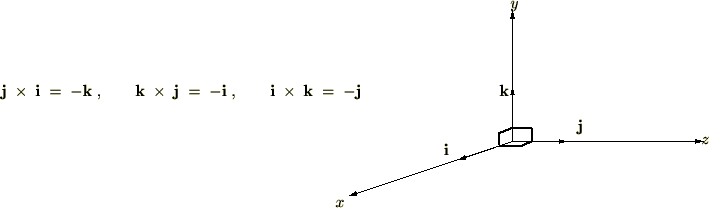
以上をまとめると、

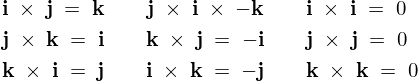
ここで式の成分にこれらをそれぞれ当てはめていけば、

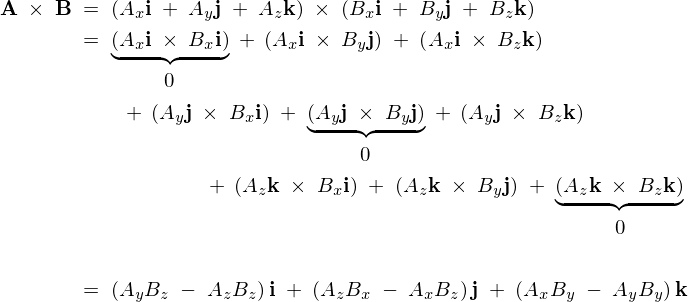
よって２つのベクトルの単位ベクトルによる表現は、

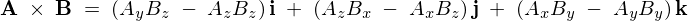
外積の幾何学的意味（面積ベクトル）

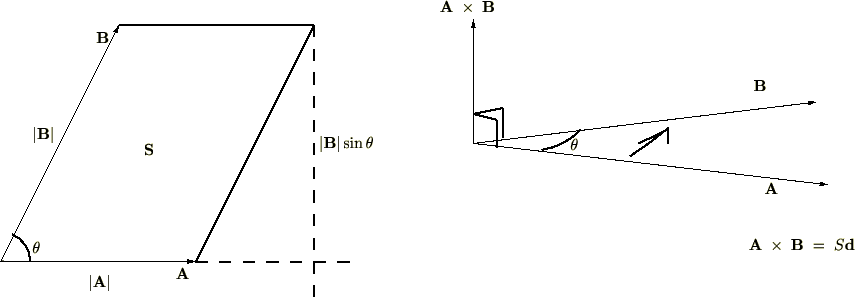
との作る平面に垂直で、からへまわした右ねじの進む向きの単位ベクトルをとすると、

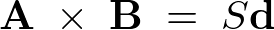
といったかたちに書けます。

左上図における平行四辺形の面積をとすれば、

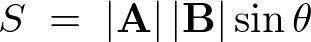
つまりと同じということになります。

よってとの外積は、

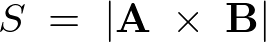
と表現できることになります。