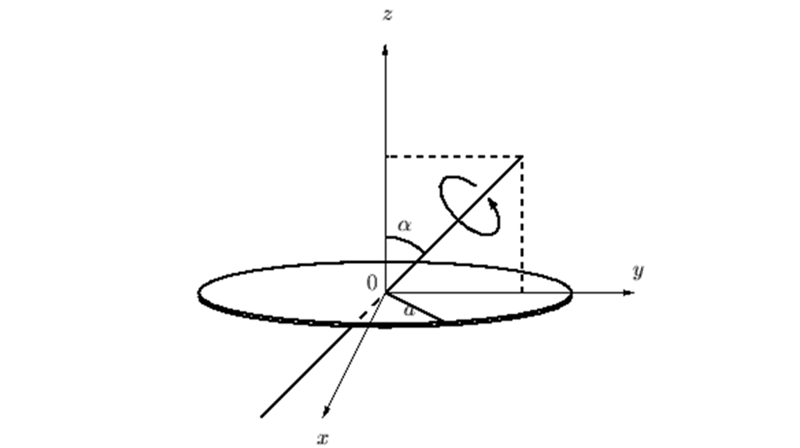
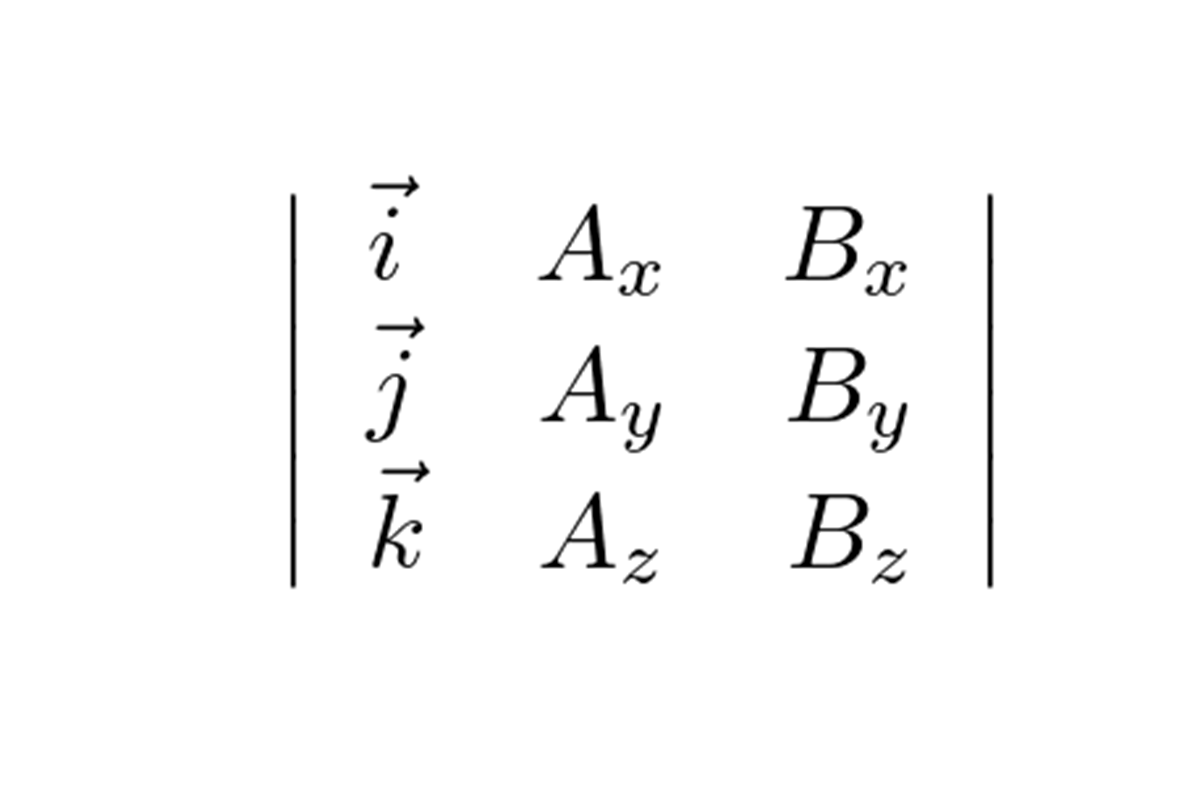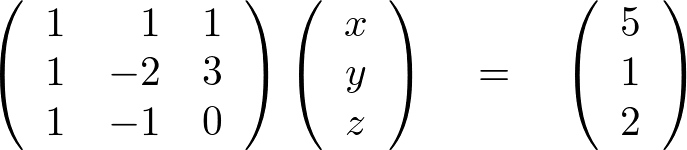三次元ベクトル場および発散についての補足
三次元におけるベクトル表現は、
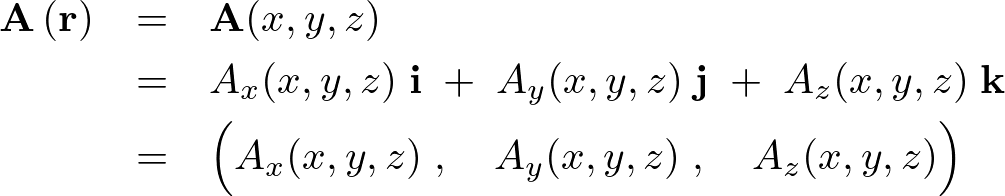
であるので、その発散は次のようになります。
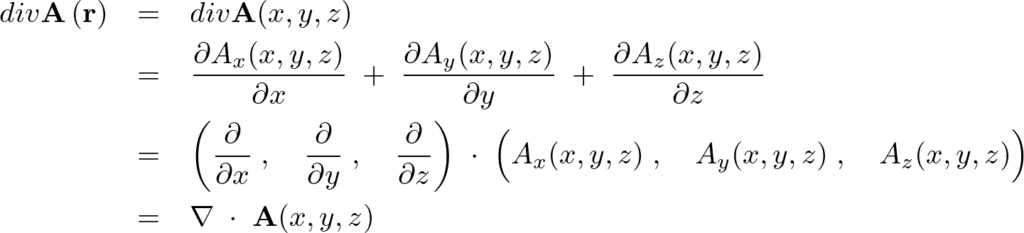
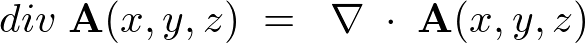
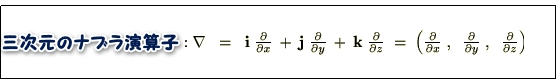
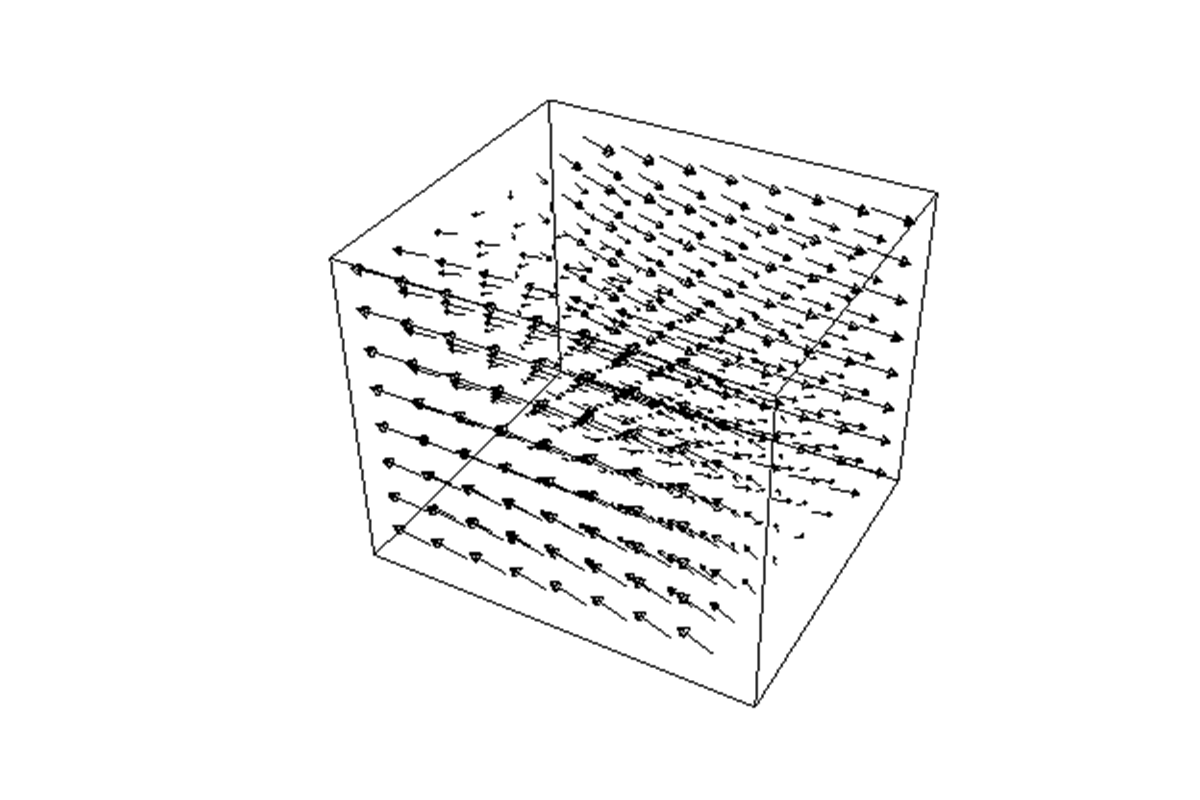
以上のことによりベクトル場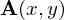 の発散(ダイバージェンス)というのは、
の発散(ダイバージェンス)というのは、
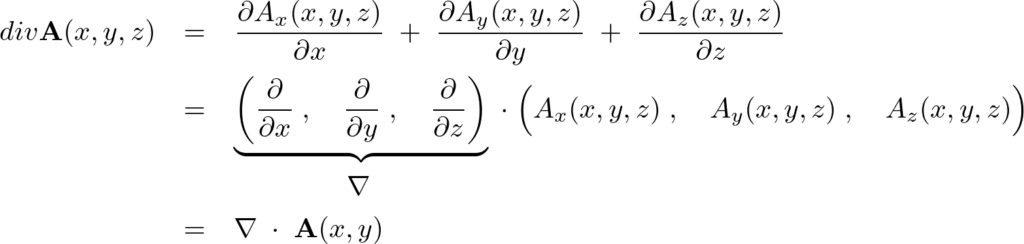
ということなので、

ということがいえます(内積なのでスカラー量)。

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
-
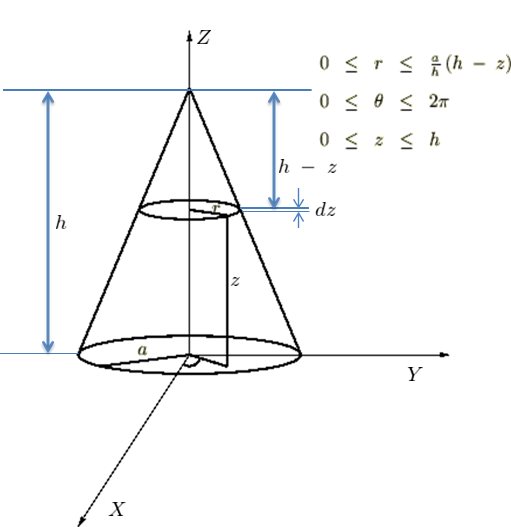
円錐の慣性モーメント
カテゴリー
-
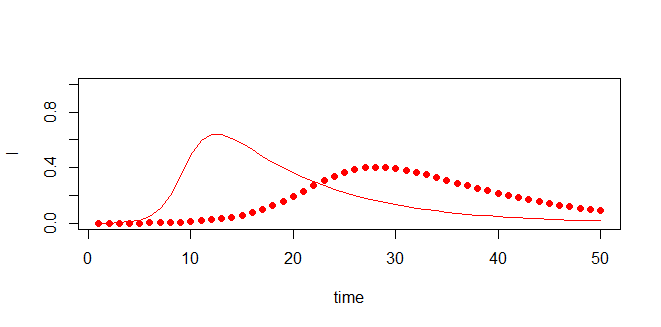
感染率による感染者数増加の比較
カテゴリー
-
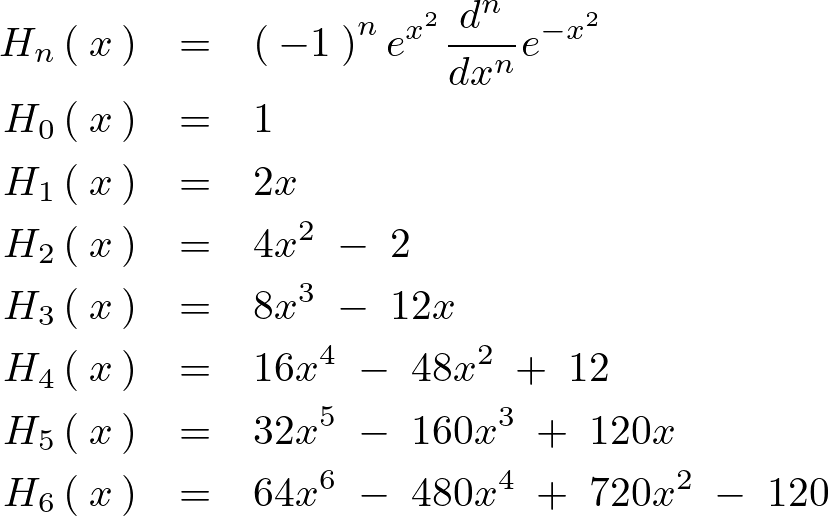
LaTeXコードの組み方
カテゴリー
-
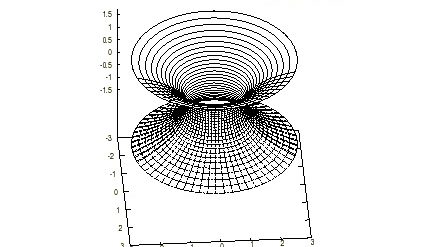
変分原理
カテゴリー
-
ラグランジュ関数
カテゴリー
-
一階常微分方程式
カテゴリー